顺滑地进入群论 (Ep.1)

对于许多物理系学生而言，“群论”这个名词的出现频率是很高的，然而很多同学似乎认为群论是某种高大上的理论，认为门槛过高而不敢入门. 事实上群论的入门难度并没有想象中那么大，而它在物理上又是极其重要的. 对于初学者来说，直觉或许比严格的数学更加重要，因此我会在保证数学性的同时用更加“物理”的方式介绍群论的基础内容.

本文是这个系列坑的第一篇，主要包含一些基础概念的直观理解.

引入“群”这个概念的初衷是为了描述对称性——在物理上，许多物理定律都可以直接由某些对称性直接导出，因此一个好用的描述对称性的理论是非常受到物理学家们青睐的.

他们为这个看似很特殊的集合起了一个这么平常的名字，可见在他们眼中这个概念有多么根本.

在自然界中，对称性或许是我们能够接触到的最接近“基本理论”的东西了（至少现在看来是的），比如我们再熟悉不过的能量守恒定律和动量守恒定律，它们分别对应着时间和空间的平移对称性. 在细致讨论前，我们先明确以下什么是对称性：

在物理上， 对称性指一个系统经过某个过程后保持不变的性质.

读起来有些拗口，我们还是用能量和动量守恒的例子.

能量守恒定律所对应的对称性是时间平移对称性，这是说：一个封闭系统的拉格朗日量 在经过一段时间 后不变，即 通俗来讲，就是说物理规律在不同的时刻是一样的.

动量守恒定律所对应的对称性是空间平移对称性，和时间类似，这是说：物理规律在不同的空间位置是相同的.

在琢磨细节之前，我们先直接说明群的定义：

一个群 就是一个集合 与这个集合中任意两个元素间的某种运算（记作“ ”），它们必须满足以下几个条件：

在上面的定义中，我们并没有说明这个 到底是什么东西的集合，我们知道的仅仅是，它就是一个集合. 同样，我们也没有说明“ ”这个运算是个什么运算. 这样模糊的定义就是一种优势——它可以用于描述任何东西，只要满足条件.

由于我们讲的是物理，所以比起“运算”，我更喜欢用“操作”这个说法. 在上面的时间平移对称性中，我们关心的操作是“让时间由 变为 ”的这个操作. 那么时间平移对称性的表述就变为：

当对系统施加一个“让时间由 变为 ”的操作后，系统保持不变.

类似地，物理系统中可以存在许多不同的对称性， 每种对称性都对应着这样一个“操作”，以及操作的对象. 这就是引入“群”概念的原初动机. “操作”对应着“ ”，操作的对象就是群 中的元素. 下面我们用一个具体的例子来说明一下：

假如有一个氢气分子 ，它长图中的样子.

图1: 一个氢气分子

为了方便，我把两个氢原子连线的中点 标出来. 正如一开始所说，群论的引入是为了描述对称性的，那么我们看看这个氢气分子中有哪些对称性. 显然，我们可以找到以下的对称性：

1. “关于长轴旋转任意角度”操作不会改变系统.
2. “围绕 点旋转 的整数倍”操作不会改变系统.
3. “沿 点镜像翻转”操作不会改变系统.
4. “在氧气中点燃并将产物电解”操作不会改变系统（某种程度上）.
5. “点赞关注本文作者”操作不会改变系统.

除此之外，这个系统还存在许多对称性，但我们并不关心所有的对称性.

实际上，上面的例子就体现出了群的四个性质：

• 封闭性：系统的操作对象是两个氢原子的状态，在这个群的范围内，无论施加何种操作都不会让这个操作对象消失（比如变成氦原子）.
• 结合性：连续施加上述对称性中的操作，系统仍然是不变的. 可见操作的顺序并不那么重要.
• 幺正性：对系统施加一个“什么都不做”的操作，系统显然是不变的. 这个操作就是 .
• 可逆性：将系统旋转一个角度，我可以把它再转回来，这就对应着 与 .

在介绍同构与同态的定义前，我们先看一个例子：

考虑一个等边三角形

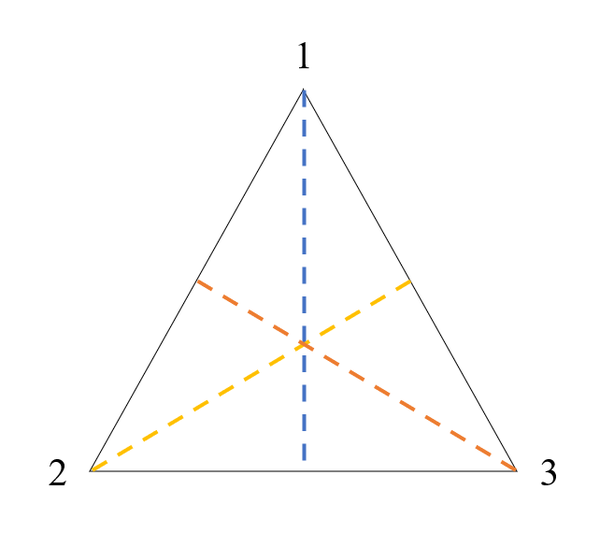
图2: 等边三角形

我们将它的三个顶点分别标上序号 （仅仅是为了方便，在几何意义上这三个顶点仍然是等价的）. 对于一个有限群 ，我们发现它有含有：

1. 顺时针分别旋转 的对称性.
2. 逆时针分别旋转 的对称性.
3. 分别沿三条对称轴镜像翻转的对称性.

此时，聪明的你一定发现，除了用上面这种表示方法，我们还可以用一个有限交换群 来表示这个系统的对称性：

我们将最初的状态用三个顶点的位置来表示，记为 . 那么不难发现，顺时针旋转 的操作就等价于将原来的 与 调换， 与 调换， 与 调换，此时的状态为 .

同样地，将三角形沿蓝色的对称轴翻转，等价于 .

经过这样一番操作，我们发现以上的两种表示方式其实是完全相同的. 有趣的地方在于，同一个系统的对称性很多时候可以用两个不同的群来表达，或者说，同一个群可以用于描述很多不同系统的对称性.

在上面的例子中， 的元素是一个等边三角形和一些几何操作， 的元素是三个实数和一些排序操作. 单独看这两个群似乎没有任何关系，但就像上面分析的那样， 它们的元素之间存在一一对应的关系. 对于这样的两个群，我们就说它们是 同构 的. 换句话说，两个同构的群内具有相同的运算结构，即使它们最初所描述的事物和操作方式可能不同.

事实上，群同构的严格定义如下：

考虑两个群 和 . 如果存在一个双射 满足 则 和 被称为是 同构 的.

而 同态 的概念相对同构就宽松一些了，它不要求 是一个双射.

同构区分于更加笼统的同态的地方主要在于：

1. 同构群中不同元素的像一定不同，而在同态群中，某个像可能来自于多个不同的元素.
2. 如果两个群同构，那么其中一个群的任意一个元素一定是另一个群中某元素的像.

^ Sadri Hassani (1998). Mathematical Physics: a modern introduction to its foundations. Springer-Verlag.

^ K. F. Riley, M. P. Hobson, S. J. Bence. Mathematical Methods for Physics and Engineering. Cambridge.