1.2 自旋、反粒子与量子场

自旋是粒子具有的一种内禀角动量，它是粒子的最重要的属性之一。当然，必须要指出它和经典力学中的自转毫无关系。自旋这个概念不是由哪个天才一拍脑袋想出来的，它的诞生与几个重要的实验结果密切相关。

首先是 碱金属光谱双线 。19世纪初随着光学仪器的发展，人们已经可以分辨出光谱中挨得很近的谱线。在这样的时代背景下，德国物理学家夫琅禾费用自制光谱仪观测并记录了太阳光谱中的五百多条暗线，史称夫琅禾费线，在这些谱线中就包括著名的钠双线（ 钠元素的两条挨得很近的特征谱线 ）。不过在19世纪人们并没有对钠双线之类的碱金属双线有太多关注，因为那时候大家不知道原子光谱的原理，所有谱线都没法解释，所以碱金属双线的理论疑难就没有显露出来。直到玻尔模型提出之后，人们才发现对于碱金属原子没法解释为什么某个位置本该是一条谱线但实际却看到了两条。

第二个实验是 反常塞曼效应 。1896年塞曼发现将原子置于磁场当中，它的某些谱线就会从一条分裂为三条，这称为（正常）塞曼效应。然而1897年普雷斯顿发现磁场中的原子谱线的分裂数还可以不是三条，于是就把这叫做反常塞曼效应。正常塞曼效应可以由磁场中玻尔原子的能级分裂解释，但这会推导出谱线分裂数只能为三条，不能为其他的数字。这样一来反常塞曼效应就变得难以理解，在1925年以前人们就没找到过合理的解释。

第三个实验结果是 斯特恩-盖拉赫实验的偶分裂数 。上一节中说到1922年的斯特恩-盖拉赫实验验证了原子角动量的量子化，但这仅仅是此实验的重要结论之一，它的另一个重要结果就是在实验中出现了与玻尔理论不符的偶分裂数结果，这暗示了半整数量子数的存在。为了理解这一点，让我们仔细看一看这个实验的内容。一个热源将银原子射出，经过隔板筛选出平行的一束后，通过一个不均匀的磁场，最终打在屏幕上。由于磁场沿z方向不均匀，即 ，所以银原子在射入磁场之后会受力 ，最终导致其偏转，在接收屏上显示出沿z方向的分布。

如果原子的角动量不是量子化的，那么 的取值将是连续的，我们会看到银原子的屏幕上沿z轴连续分布，如图1的(2)屏。但实际上，在实验中我们看到屏上的银原子沿z轴的分布是不连续的几段，这就说明原子的角动量确实是量子化的。根据玻尔理论， 正比于磁量子数 ，而 和角量子数 有关（ 是非负整数），其取值范围 ，例如 时 。可以看到，玻尔理论中磁量子数 只能是奇数个，所以 只能是奇数个，使得此实验中银原子只有奇数种受力情况，因此按理说银原子束在屏幕上只能分裂成奇数段。然而在实验中却看到银原子束分裂为了偶数段，这意味着可能存在与角量子数 类似的半整数量子数 ，使得其磁量子数 取值为偶数个，例如对 有 。

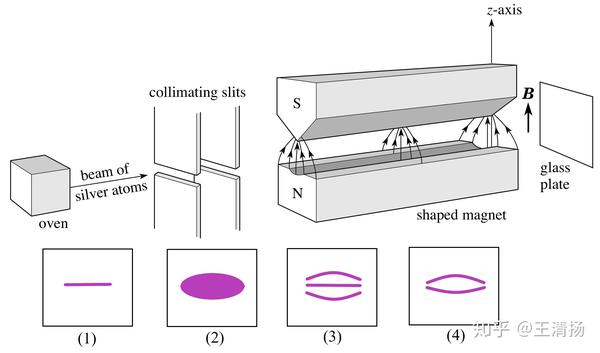图1 斯特恩-盖拉赫实验。证实了原子的角动量量子化，且发现可能存在与角动量类似的半整数量子数。（1）不加磁场时银原子束不分裂；（2）加磁场，经典物理预言银原子束的上下分布是连续；（3）加磁场，玻尔的量子理论预言银原子束会分裂为奇数段；（4）加磁场，实际观察到银原子束分裂为偶数段。

既然可能存在半整数的量子数，那么就要问了：这个量子数是谁具有的呢？抛除了一切其他可能性之后，这个重任落到了原子中的电子身上，也就是说电子要具有 内禀角动量 。1925年，克罗尼格首先想到电子可能存在自转使其具有内禀角动量 ，但这一想法遭到了海森堡、泡利等人的反对，于是他没有将其正式发表。到了这一年的年底，乌仑贝克和古兹密特也产生了这样的想法，他们写了一篇论文交给导师埃伦费斯特，然后去请教洛伦兹。洛伦兹计算后告诉他们，如果电子是个有自转的球体，想达到如此大的磁矩，它的表面速度将会超光速（ 实际上，以现在的观点看电子根本不是个球，自然不会有表面超光速这种事 ）。二人听后大吃一惊，立马回去找导师想要追回论文，但此时埃伦费斯特已将论文寄出。当时二人就傻眼了，埃伦费斯特只好安慰他们说：年轻人嘛，做点蠢事没关系。

然而，电子自旋提出后很快得到了大家的支持，因为它完美地解决了碱金属双线、反常塞曼效应以及斯特恩-盖拉赫实验的疑难。就连海森堡也只能感叹：哎呀，真香！（ 海森堡的原话：如果没有古兹密特，我们真不知该怎么处理塞曼效应。 ）至于泡利，虽然他依然反对电子自旋的物理图像，但他也意识到自旋这个量子数和自己在1925年初提出的 不相容原理 中所要求的一个二值性量子数十分类似。不相容原理最初是指每一个确定的能量本征态上最多只能容纳一个电子，然而在实验中却发现了一个能态上有两个电子的情况，比如氦原子的同一个能级上有两个电子。由此泡利认为电子应该还有另一个二值性的量子数，现在他意识到了这个量子数就是自旋。怀着完善自旋的目的，泡利于1927年构造了描述自旋的泡利矩阵（ 现在我们知道这是自旋 算符在 表象下的矩阵表示 ），并用它得到了电磁场中电子的运动方程。这样一来就可以计算电磁场中原子的各种效应，极大地推动了原子物理与量子力学的发展。

最后关于泡利的不相容原理再多说两句。首先这个原理对理解元素的化学性质是非常有用的，它直接决定了每种原子每个能级上能存在的电子数量，由此可以导出化学中的元素周期律。此外，不相容原理还可以推广至全体自旋为半整数的粒子，而不仅限于电子，这可以推出粒子自旋与大量粒子的统计规律之间的关联。对于自旋为半整数的粒子，不相容原理使它们不能聚集在同一个态上，这样可以导出它们满足一种被称为费米-狄拉克统计的统计规律，由此半整数自旋的粒子也被称为 费米子 。而对于自旋为整数的粒子，一个态上能聚集的粒子数没有限制，因此它们满足一种被称作玻色-爱因斯坦统计的统计规律，被称为 玻色子 。这些统计规律直接决定了我们看到的宏观现象，例如黑体辐射谱、固体的热容、材料的导电性等。也就是说，量子力学其实无处不在，很多我们习以为常的宏观现象本质上可能是由自旋这样的量子效应决定的。

从物质构成的角度来分析，费米子是 “组成物质” 的基本粒子，例如电子，质子，中子这些都是费米子，而波色子是在不同的费米子之间传递相互作用的，玻色子有点像不同费米子之间的粘合剂。可以设想，我们的宇宙是一个巨大的建筑，建筑由不同的材料构成：砖头，石板，水泥板，钢筋混泥土...，这些材料都是费米子，可是如何把这些材料组建在一起建立一座大厦呢？建筑工人会使用一系列“基本方法”把不同的材料粘合在一起，用砖头建成墙面，用墙面建成房间，用房间建成楼层，楼层组成大楼，每一层的组装都需要用不同的“基本方法”，这些“基本方法”对于我们宇宙而言就是不同的“基本相互作用”，而这些基本相互作用就是由玻色子来传递完成的，例如光子，胶子，W粒子都是玻色子。
从性质上来分析，费米子是半分数自旋，玻色子是整数自旋。玻色子的这种性质使得它很容易被用一个场来表示，实际上，标准模型中的规范场都是玻色子场，满足洛伦茨对称性，而费米子则直接使用波函数来表示。
玻色子和费米子的运动方程也不一样。费米子直接使用狄拉克方程，玻色子则是Klein Gorden方程，由不用类型的作用量求变分得到。费米子有泡利不相容原理，导致了费米子的研究方法会更复杂一些。
进入多粒子系统，它们的差异就更大了。现代凝聚态理论的研究中，玻色子的多粒子系统与费米子的多粒子系统的研究方法差异比较大，一般来说后者更困难一些，因为费米子有不相容原理，导致了多粒子系统的反对称性，需要引入Grassmann代数这种特殊的工具，而玻色子多粒子系统则没有这种需要。 https://www.zhihu.com/question/344167022/answer/1771316649

虽然自旋这个概念很快被人们接受，但仍有两个问题需要被回答：（1）自旋是从哪来的？或者说从什么基本理论可以导出粒子的自旋？（2）自旋真正的物理图像是什么？（ 小球自转肯定不对... ）相对论性量子力学可以回答第一个问题，第二个问题要由量子场论去回答。为方便起见，从现在开始我们采用自然单位制，即令 。

1.1节中说过薛定谔方程 是非相对论的，它的哈密顿量采用的是非相对论的能动量关系，对自由粒子有 所谓的相对论性量子力学，其实就是想办法构造一个满足相对论性能动量关系 的波动方程。最简单的想法就是将相对论性的 替换入薛定谔方程： 与薛定谔方程一样，这个方程也是描述一个物质波 如何随时间演化，只不过薛定谔方程描述的是非相对论的波，而这个方程描述的是符合相对论的波。在1.1节中我们提到薛定谔最先构造的是这种相对论性的波动方程，结果他发现这个方程无法应用于氢原子，之后选择去构建了非相对论的薛定谔方程。这使得此方程最终以另外两个独立发现它的科学家的名字命名—— 克莱因-戈登方程 （K-G方程）。然而，K-G方程的问题不仅在于不能描述氢原子中的电子，它还有其他更严重的问题。首先，它存在负能量解，这使得体系能量无底线，粒子会一直向更低的能量跃迁，因此没有一个稳定的真空。第二，K-G方程中存在负概率问题（ 波函数的模平方为负 ），这直接挑战了波函数的概率诠释。第三，K-G方程破坏了因果性。这些问题使得人们开始思考能否构建其他形式的更合理的相对论性波动方程。

1928年，狄拉克构造了一个这样的相对论性波动方程： 狄拉克方程 与K-G方程的不同之处在于，它是一个一阶的微分方程，且波函数 具有多个分量。在与电磁场耦合之后，狄拉克的方程可以完美地描述氢原子中的电子，甚至给出了氢原子光谱的精细结构（ 也就是前面说的碱金属双线 ）。为什么狄拉克方程可以描述电子，而K-G方程却不可以呢？回答这个问题需要计算两个方程对应粒子的角动量。计算狄拉克粒子的角动量我们发现其守恒的角动量分为两个部分，一部分是我们熟知的轨道角动量，另一部分是大小为1/2的内禀角动量，显然后者正是电子这样的费米子的自旋。而计算K-G粒子的角动量得到的结果只有一项轨道角动量，因此K-G方程描述的是自旋为0的粒子，自然无法描述电子。至此，我们知道了电子的自旋从哪里来——从它的相对论性波动方程中来。

狄拉克方程的另一个成功之处就是暗示了 反粒子 的存在。与K-G方程相比，在狄拉克方程中负概率问题被解决了，但负能量解依然存在。然而狄拉克认为负能态就像大海一样，里面被电子这样的费米子填满了。根据泡利不相容原理，两个电子不能处于同样的状态，因此正能态的电子无法跃迁到已被电子填满的负能态，这使得真空稳定。那么反粒子在哪里呢？狄拉克认为，负能态的电子海也可以不被填满，里面可以有一些没有装填电子的空位置，这样的位置被称为空穴。空穴可以在负能态海中自由移动，就像一个个粒子一样。当正能态的电子遇到一个这样的负能空穴时，它会跃迁入负能态，从而释放出两倍于它自身的能量的光子。简而言之，就是说电子遇到负能海中的空穴会湮灭为光子。狄拉克将这个假想的空穴称为电子的反粒子，它有着与电子相同的质量，但由于电荷守恒，这种反电子的电荷与电子相反（ 这样它俩才能湮灭为不带电的光子 ）。虽然狄拉克的这个猜想看起来非常扯，但它竟然被实验证实了！1932年，安德森在云室实验中发现了一个荷质比与电子相反的粒子，这正是狄拉克预言的反电子。在此之后，其它费米子的反粒子（如反质子）也陆续被发现。（ PS：有些书中根据电子的反粒子带正电称其为正电子，也是可以的，正电子和这里的反电子是一个意思。 ）

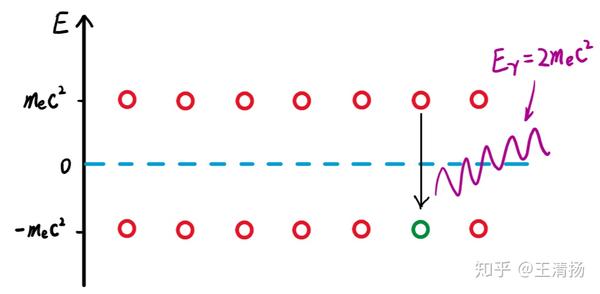图2 狄拉克海与反粒子。图中红色圆圈是电子，能量E=0的海平面上方是处于正能态的电子，海平面之下是处于负能态的电子。负能海中没有电子的空位置（绿色圆圈）被认为是电子的反粒子，处于正能态的电子跃迁至这个空穴时，相当于电子与与其反粒子碰撞，它们湮灭产生能量为2倍电子能量的光子。

解释了自旋的来源，预言了反粒子，狄拉克方程彰显出其巨大的威力，然而这样一个理论仍不是完美的。首先，对于因果性问题，狄拉克方程依然无能为力，因果律在这里仍被破坏。第二，虽然狄拉克方程暗示了反粒子，但电子海与空穴的假设实在是太过魔幻，有可能我们得到了正确的结果但采取了错误的理解方式。第三，也是最重要的，不论是K-G方程还是狄拉克方程，它们都可以导出粒子数守恒的结论，无法描述粒子的产生湮灭过程。因此在相对论性量子力学的尝试中，虽然狄拉克方程比K-G方程进步了很多，但它仍是一个有问题的理论。

相对论性量子力学的种种困难暗示着我们需要一种更加合理的描述微观物质的模型，也就是说我们需要重新理解各种波动方程的意义。前面一直在说波动方程描述的是一个波 在时空中的演化，然而 并不只有“波”这一种解读方式，它还可以被解读为在时空中分布的“场”。如果我们把各种相对论性波动方程解读为时空中的经典场方程（ 例如认为K-G方程是标量场的场方程，狄拉克方程是旋量场的场方程，麦克斯韦方程是电磁场的场方程 ），再对“场”这种无穷自由度的系统做量子化，同样可以得到一个满足狭义相对论的量子理论—— 量子场论 。

量子场论的历史可以追溯到1926年，玻恩、海森堡、约当利用正则量子化方法将电磁场量子化，构建了电磁场的量子理论。所谓的正则量子化，其实就是将1.1节中的位置-动量的不对易关系（ 称为正则对易关系 ）应用于电磁场中： 从而得到一个可以让光子产生湮灭的量子理论。1930年前后，正则量子化方法被应用于K-G场和狄拉克场，人们构建了这两种场的量子理论。事实证明，量子场论是一个非常漂亮且自洽的理论。首先，它完美地克服了相对论性量子力学的困难，负概率消失，负能量解消失，可以描述粒子的产生湮灭，因果性也被很好地保持了。同时，量子场论可以更加准确地描述反粒子，将消灭一个负能的电子可以诠释为产生一个正能的反电子，而不需要采用狄拉克海之类的魔幻的概念。此外，人们还惊奇地发现量子场论可以解释泡利的不相容原理——它的根源在于狄拉克场的量子化需要使用反对易关系（ 也就是把对易关系的乘积相减改为乘积相加 ）：
量子场论还可以为波粒二象性和自旋的概念给出一种合理的物理图像。在量子场论中， 所有物质都是弥漫在时空中的场 （例如电磁场） ，场方程的解对应时空中的波，这种具有波动性的场的能量是分立的。场的能量每上升一个台阶就相当于时空中激发出一个粒子，每下降一个台阶就相当于时空中湮灭一个粒子。也就是说场是比粒子更基本的东西， 粒子是具有波动性的场的激发态 （ 比如光子是电磁场的激发态，电子之类的费米子是狄拉克场的激发态 ）。这样一来就把粒子和波这两种图像结合在了一起，给出了波粒二象性的物理图像。至于自旋，既然场比粒子更基本，那么 粒子的自旋就可以被理解为场的内禀角动量 。一个很好的例子是光子的自旋，光子作为电磁场的激发态，它的自旋就是电磁场方向转动所带来的角动量。如下图所示，可以看到光子/电磁波沿直线运动，运动方向不发生改变，但场的方向一直在周期性改变。其他粒子的自旋也可以以同样的方式去理解，所以粒子自旋不是小球自转，它是粒子对应的场在转动。

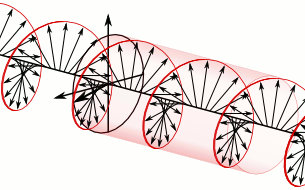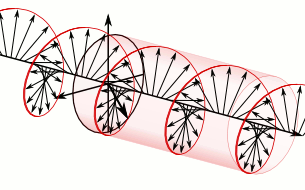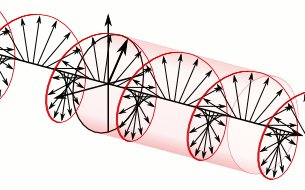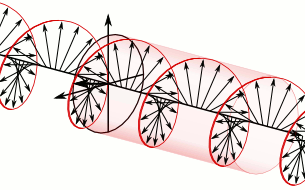
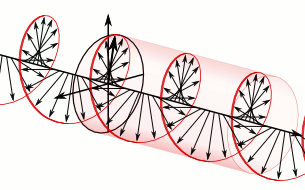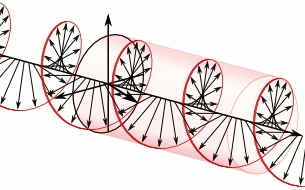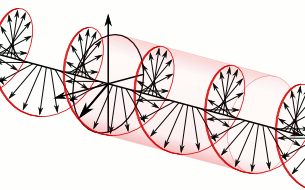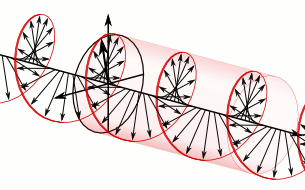图3 自旋s=1的光子（图片来自网络）。上图为ms=+1的右旋光子，下图为ms=-1的左旋光子。可以看到粒子沿一条直线运动，它所对应的场的方向（箭头）一直在周期性改变，这导致了自旋这个量子数的存在。

前面提到的K-G场、狄拉克场、电磁场都是描述自由粒子的自由场，不涉及相互作用。为了研究粒子的散射、衰变等问题，人们必须要构建一套包含场的相互作用的量子场论。而在微观世界最常见的相互作用就是带电荷的费米子之间通过电磁场进行相互作用，或者带电荷的费米子与光子的相互作用，这些情况统称为电磁相互作用。这样一个关于电磁相互作用的量子场论被称为 量子电动力学（QED） ，它的核心在于我们要在系统的拉氏量（ 描述物理系统的一个函数 ）中写下狄拉克场与电磁场的耦合项。考虑到狄拉克场和电磁场的U(1)规范对称性，可以将它们的耦合项写为： 其中 是狄拉克场， 是狄拉克场的共轭， 是电磁场，也就是说QED的每一个相互作用顶点都涉及两个费米子和一个光子，任何电磁相互作用过程都可以用这样的顶点的组合表示出来（ 专业术语叫做S矩阵的微扰展开 ）。

看到这里，读者可能会感到懵圈，毕竟我第一次学量子场论的时候也被这些涉及相互作用的东西搞晕了。其实这些东西有一种非常便于理解的表示方法—— 费曼图 ，这是天才物理学家费曼发明的一套用于表示粒子间相互作用的示意图。上述的耦合项 ，也就是QED的相互作用顶点，用费曼图可以表示为图4(a)，可以看到两个费米子和一个光子耦合在这个顶点上，这是构成所有电磁相互作用过程的最基本单元。图4(b)(c)(d)给出了一些简单的电磁相互作用过程，它们都由图4(a)的基本单元组成，图的注释给出了这些费曼图的物理意义。当然，这些过程都是最低阶（ 树图 ）的过程，高阶过程的费曼图会出现封闭的圈（ 圈图 ），有兴趣的读者可以参考任何一本量子场论书。另外还有一点需要注意，费曼图表示物理过程不一定代表经典的过程。比如图4(b)不能理解为一个电子吐出一个光子被另一个电子接收，因为这里的光子是两端都为顶点的传播子，它是一个 虚粒子 ，并没有真的在时空中出现，因此仅仅是作为在两个电子之间传递电磁相互作用的纽带。同理图4(c)中间的费米子传播子也是虚粒子，没有真正在时空中出现。关于费曼图的内容先说这么多，我们先不深究它和物理可观测量的关系，暂时只需要知道它可以表示粒子间的相互作用就可以了，在后面的章节中会更详细地介绍它。

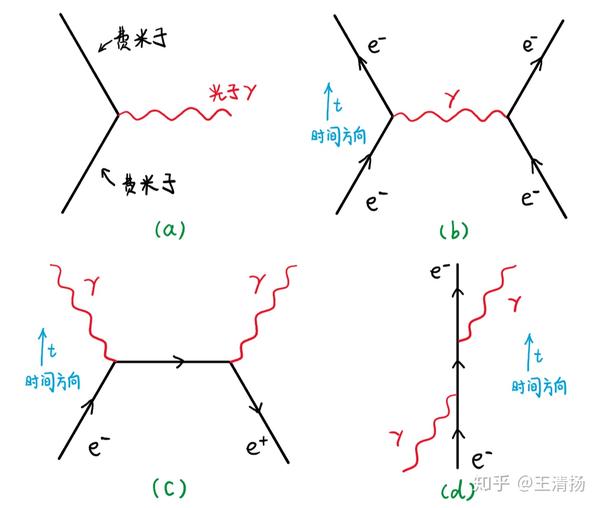图4 量子电动力学QED的一些最低阶费曼图。(a)QED的相互作用顶点，两个费米子和一个光子耦合在这个顶点上，这是构成QED过程费曼图的最基本单元；(b)电子与电子通过交换虚光子进行散射的过程；(c)正负电子通过一个虚费米子湮灭为两个光子的过程；(d)电子与光子的康普顿散射过程。

随着QED在上世纪三十年代逐步形成，量子场论的一个重大问题开始浮现出来—— 发散 。所谓发散，就是说量子场论的计算结果经常会出现无穷大（ 尤其是圈图的计算结果 ），比如计算电子的电磁自能的结果就是无穷大，这是物理学中不允许的。一开始人们觉得计算出的发散物理量可能实际上都等于零，但是1947年在原子光谱实验中发现的兰姆移位现象表明，这些在计算中发散的物理量实际上不是零，它们拥有可测量的具体数值！这使得量子场论的发散问题必须被重视起来。1947-1949年，施温格、费曼、朝永振一郎等人建立了一套处理发散的理论方法，被称为 重整化 方法。QED在结合了重整化方法后，可以有效地消除计算结果的无穷大，准确地对兰姆移位以及的电子反常磁矩等现象进行计算，结果甚至可以精确到小数点后10位！至此，一个完整自洽的关于电磁相互作用的量子理论正式确立，人们对微观世界的认识进入了新纪元。

本节的故事讲到这里基本上就结束了，如果读者想了解相对论性量子力学以及早期量子场论的更详细的历史，可以参考温伯格《量子场论》第一卷第一章。虽然到此为止只带大家认识了光子、电子、反电子以及原子核这些粒子，但有了量子场论的这个框架，人们很快就可以向微观世界的其他相互作用进军，迎来粒子物理的大爆发。在下一节我会介绍强相互作用与弱相互作用的研究历史，与大家一同回顾粒子物理的标准模型大厦的搭建过程。

本节内容的概念要点总结如下：

1. 相对论性波动方程 ：在相对论性量子力学的框架下，是一种结合狭义相对论与量子力学的波动方程，包括描述自旋0粒子的克莱因-戈登方程，描述自旋1/2粒子的狄拉克方程以及描述自旋1光子的麦克斯韦方程等。在量子场论的框架下，被理解为满足相对论协变性的场的经典场方程，上述三个方程分别描述标量场、旋量场以及电磁场。
2. 量子场论 ：量子力学是关于有限自由度的粒子的量子理论，而量子场论是关于无穷自由度的场的量子理论。量子场论认为所有物质都是弥漫在时空中的满足相对论协变性的场，场比粒子更基本，粒子是具有波动性的场的激发态，可以产生也可以湮灭。
3. 自旋 ：粒子具有的一种内禀角动量，它来源于粒子的相对论性波动方程/场方程，可以理解为粒子对应的场本身在转动。自旋为整数的粒子称为玻色子，自旋为半整数的粒子称为费米子。费米子满足泡利不相容原理，不能在同一个态上聚集。
4. 反粒子 ：粒子对应的一种质量、自旋和它相同，但电荷与其相反的粒子。狄拉克首先通过假想的负能海的空穴预言了它，但在量子场论中它被重新解释。正反粒子相遇可以散射，但更多情况下它们会湮灭到一对光子。
5. 量子电动力学QED ：带电的费米子之间及它们与光子之间的电磁相互作用的量子理论。在QED中，粒子间的相互作用可以非常方便地用费曼图表示。QED的计算结果有时会出现发散问题，需要用重整化方法去解决。

本节内容的时间线总结如下：

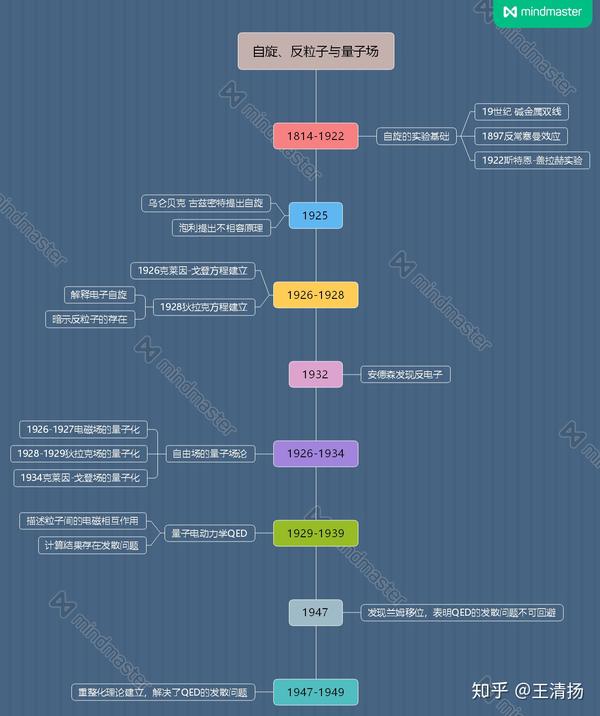
最后留几个问题给不仅仅想看热闹的读者，可以在评论区交流一下自己的想法。

1. 从狄拉克方程出发，验证电子的自旋为1/2。
   在量子力学中，如果一个力学量 是守恒的，那么它一定与系统的哈密顿量 对易： 。对于自由电子的狄拉克方程，空间转动对称性要求它的总角动量 一定是个守恒量，有 ，但计算发现它的轨道角动量 并不是一个守恒量，有 ，因此费米子一定存在除轨道角动量之外的另一种角动量，也就是自旋 ，也就是说总角动量等于轨道角动量与自旋之和 ，二者之和与哈密顿量对易。
   设自由电子狄拉克方程的哈密顿量为 ，其中c为光速常数，m为电子质量； 为动量，是个矢量，有三个空间分量； 也是个矢量，也有三个空间分量； 是个标量。引进算符 ，它满足 ， ， （例如 ）。请根据以上条件证明：如果要求总角动量 守恒，则电子自旋 。
   （ 这个问题对学过量子力学的读者来说可能很简单，没有学过量子力学的读者原则上根据这些条件也是可以算的。可以参考曾谨言《量子力学（第五版）卷II》的11.2.2节。 ）
2. 场的量子化。
   对于K-G场，引入正则对易关系与产生湮灭算符后，它的能量和动量可以写为： 其中 为产生算符，它作用于一个n阶态后将其变为n+1阶的态（ 把n粒子态变成n+1粒子态，相当于激发出一个粒子 ）： 为湮灭算符，它作用于一个n阶态后将其变为n-1阶的态（把 n粒子态变成n-1粒子态，相当于湮灭一个粒子 ）： 其中 是非负整数。试证明： 算符的取值范围（本征值）为非负整数。
   （ 这使得K-G场的能量动量均正比于非负整数 ，因此它们都是量子化的，且能量动量的间隔是等间距的，因此我们可以把场的每次激发解读为一个能量为 动量为 的粒子。）
3. 被禁戒的相互作用过程。
   根据图4(a)的QED相互作用顶点，貌似允许存在正负电子湮灭到一个光子的过程，或者一个自由的高能光子衰变到正负电子的过程，试论证这样的物理过程实际上不能发生。
   （ 提示：光子动量不能为0。 ）