有限域计算简述 - 知乎

这里的域（Field）的定义是有如下特性的集合 ：

• 定义了加法和乘法
• 集合内的元素经过加法和乘法计算，结果仍然在集合内
• 计算符合交换率、结合率、分配率
• 加法和乘法有单位元素（所有的集合内的值都有对应的负数，所有集合内非零值都有倒数）

举个例子，我们常见的实数集是域，但整数值不是域（因为除了1，其它数的倒数都不是整数）。

具有有限个元素的域就是有限域（下文以GF表示，GF是Galois Field的缩写，这个名字纪念发明者Evariste Galois)。

这可能有点反常识，既然可以一直加、一直乘，怎么会只有有限个元素呢？一个关键的操作就是‘取模’。也就是在域的定义基础上，作如下修改：

• 定义 模p加法 和 模p乘法 （加或乘的结果超过p时，模p取余数。p为素数）
• 集合内的元素经过加法和乘法计算，结果仍然在集合内
• 计算符合交换率、结合率、分配率
• 加法和乘法有单位元素（所有的集合内的值都有对应的负数，所有集合内非零值都有倒数）

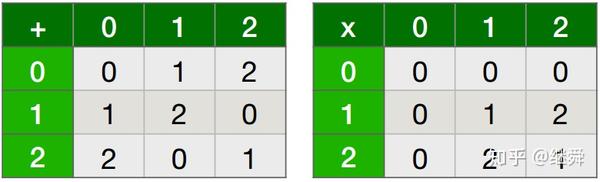
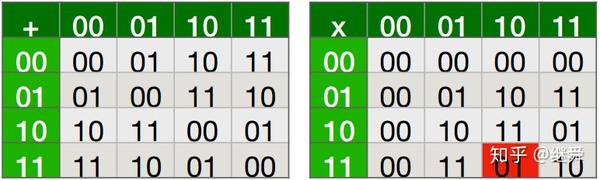
举例子，GF(3)是定义了模3加法和乘法的有限域，有三个元素：0、1、2。两个计算示例：

（另外注意以上两个计算分别说明了1、2互为‘负数’，2是2的倒数）

下面是GF(3)的加法和乘法的所有组合。

那么，如果p不是素数会怎样呢？以下面‘GF(4)’的例子来说明：

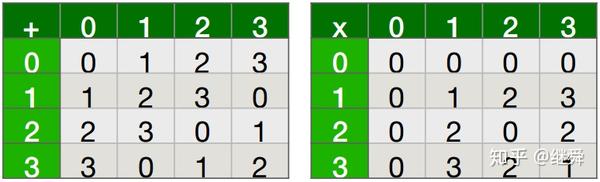
GF(4)并不是有限域的存在，因为它并不能满足所有有限域的定义要求，因为元素2没有倒数。

不过，如果我们修改一下元素，将'GF(4)'改为 ，4个元素的集合也可以成为有限域：

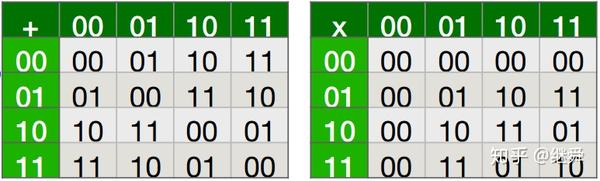
（'GF(4)'的 的区别是 在计算时每个位都是模2运算，即'异或'）

在通信编码中使用的就是 这种形式的有限域，因为二进制、加法/异或这些十分适合通信硬件实现。

下面引入多项式的概念以更好的理解 中的乘法。

二进制数可以表示成多项式的方式：

这个多项式表示中内含了高有效位(MSB)低有限位(LSB)的概念，代表的是不同位的位置权重的区别。（上面多项式中代入 就可以得到11000001代表的数值193）

有限域中加法和乘法的多项式表示可以用如下例子来说明：

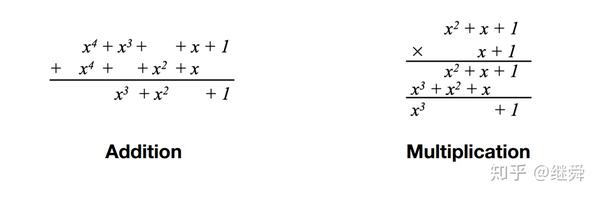
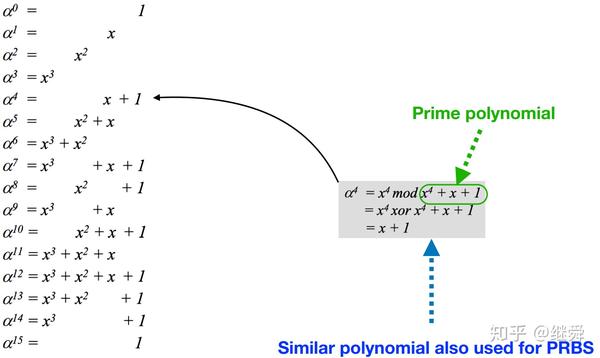
再回头看一下前面的 的例子，例子中的00、01、10、11等值用多项式表示就是：

使用取模多项式为

以上图中红色框的数值计算为例，计算过程是：