About Science
内容地图页面, 分为 数学 物理 两大主题
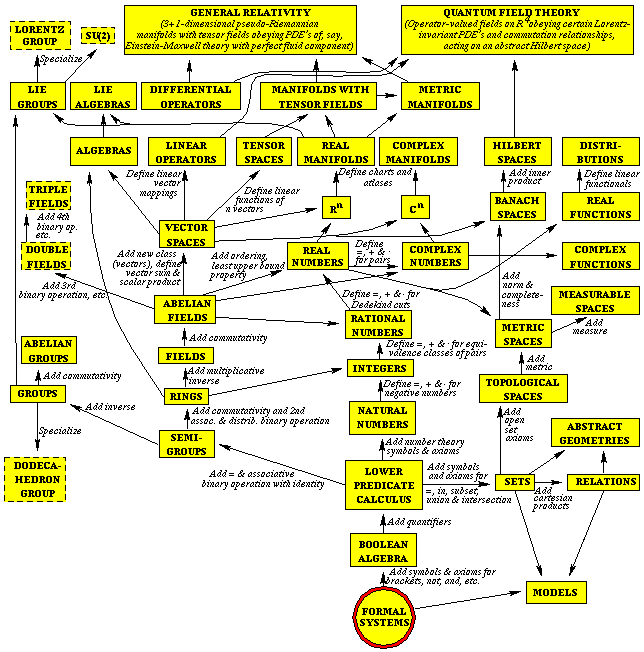
from McCabism - Pointless space
数学
总览
代数结构入门-群、环、域、向量空间-–-Spark-Shine
群论
直观理解 不涉及公式的
如何直观地理解群论? > 这个问题里的回答质量很高,很适合初学者阅读,以获得对群论的直观了解
-- 完了改名了, 又存一遍 前置内容 从映射到张量
第一个小标题是 "商群 - 群的所有1次不可约复表示" 好家伙
写的很早, 赞同数不高
没早看到这篇呢
李群
考虑分类到物理章节
芬曦丽雪:能量、动量守恒
顺滑地进入群论 Ep.1
顺滑地进入群论 Ep.2 U(1) SO(2) SO(3) SU(2)
顺滑地进入群论 Ep.3 李群与李代数
物理学中的群论 · 入门篇 第〇章:概述
物理学中的群论 · 入门篇 第一章:有限群
物理学中的群论 · 入门篇 第二章:有限群表示论
物理学中的群论 · 入门篇 第三章:转动变换群
教材
Quantum Theory of Many Particle Systems 李新征 Home--Teaching
被树推荐, 被好多人推荐
Group Explorer: 一个酷炫的群论可视化工具-CSDN博客
Group Explorer 3.0 - Visualization software for the abstract algebra classroom
该软件的作者还写了一本配套的群论科普书(Visual Group Theory),中文版为:“内森.卡特《群论彩图版》(郭小强 罗翠玲 译,机械工业出版社)”
域论
-- 一些笔记存储到 Code 仓库
取模运算本质是减法,因为要的结果是最终的余数,文中写成加法是因为对二进制运算来说加和减一个意思
RAID 算法
线性代数
Lecture 1 - System of Linear Equations
Lecture 2 - Basic Matrix Algebra
Lecture 3 - Determinants
Lecture 4 - LU Decomposition
Lecture 5 - Vector Operations
Lecture 6 - Linear Combination
Lecture 7 - Linear Independence
Lecture 8 - Vector Space and Subspace
Lecture 9 - Basis and Dimension
Lecture 10 - Column, Row and Null Space
Lecture 11 - Linear Transformation
Lecture 12 - Eigenvalues and Eigenvectors
Lecture 13 - Diagonalization
Lecture 14 - Application to Dynamic System
Lecture 15 - Inner Product and Orthogonality
Lecture 16 - Gram-Schmidt Process and Decomposition
Lecture 17 - Symmetric Matrices and Quadratic Form
Lecture 18 - Singular Value Decomposition
Lecture 19 - Multivariate Normal Distribution
微积分
变分法 #todo 这部分要不分类到物理吧
以下几篇也在物理章节
如何理解最小作用量原理?
中学生能理解最小作用量原理吗?
信息论
统计
The Book of Why 为什么 关于因果关系的新科学
此书也见 备忘 数学物理科普书收集 > 为什么 关于因果关系的新科学
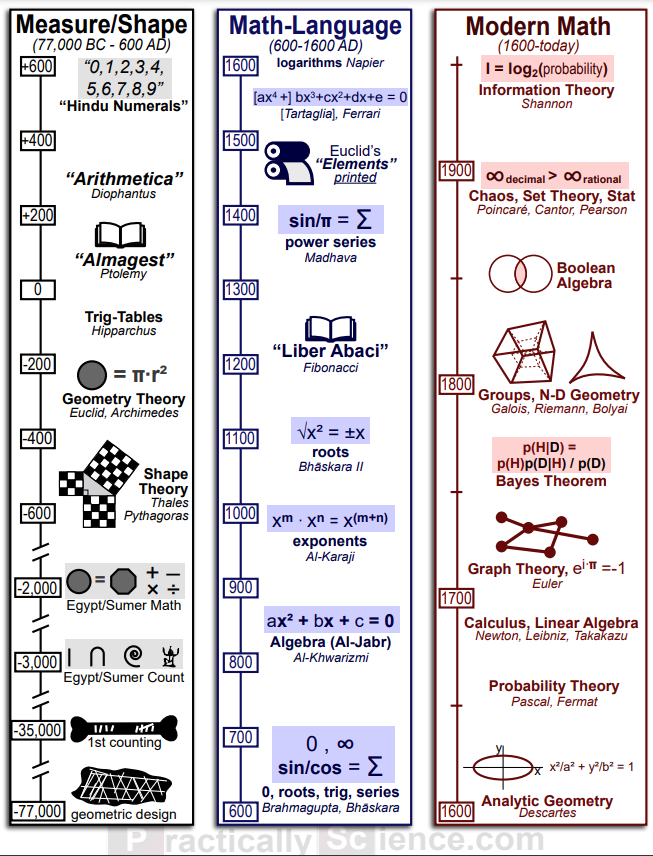
数学史
Mathematica
在线交互Notebook
https://www.wolframcloud.com/
MISC
数学家能找到定理之间的相似之处,优秀的数学家能看到证明之间的相似之处,卓越的数学家能察觉到数学理论之间的相似之处。而最顶级的数学家能俯瞰这些相似之处之间的相似之处。
「同构」是一种「态射(morphism)」 ... 在两个不同的数学结构之间,我们都可以去寻求某种抽象的方式,使得它可以保持某种数学结构,这就是在寻求「相似之处的相似之处」
- 前置 虚数 i 到底是个什么东西?2
- 前置2 怎么向小学生解释欧拉公式?1后面成人版讲怎么联系到一维酉群及李代数
考虑单独分类到计算理论
物理
历史
[file: 费恩曼物理学讲义](es:费恩曼物理学讲义 新千年版)
file: 第一推动丛书 复杂复杂的引擎皇帝新脑逻辑的引擎数学的意义未来50年真理与美
唯象理论(phenomenology),是物理学中解释物理现象时,不用其内在原因,而是用概括试验事实而得到的物理规律。唯象理论是试验现象的概括和提炼,但仍无法用已有的科学理论体系作出解释。即“知其然而不知其所以然”(知道事情的结果,却不知道造成结果的原因)。唯象理论对物理现象有描述与预言功能,但没有解释功能。最典型的例子如开普勒三定律,就是对天文观测到的行星运动现象的总结。实际上支配开普勒三定律的内在机制是牛顿的万有引力定律。进一步层次,牛顿的万有引力定律也是唯象的,需要用广义相对论去解释。若推广到量子层面,即量子引力理论,则为一个物理学家尚未解决的问题。
杨振宁把物理学研究分为三个阶段:试验、唯象理论、理论架构。
分析力学
变分法 是处理泛函的数学领域,和处理函数的普通微积分相对。譬如,这样的泛函可以通过未知函数的积分和它的导数来构造。变分法最终寻求的是极值函数:它们使得泛函取得极大或极小值。有些曲线上的经典问题采用这种形式表达:一个例子是最速降线,在重力作用下一个粒子沿着该路径可以在最短时间从点A到达不直接在它底下的一点B。在所有从A到B的曲线中必须极小化代表下降时间的表达式。
变分法的关键定理是欧拉-拉格朗日方程。它对应于泛函的临界点。在寻找函数的极大和极小值时,在一个解附近的微小变化的分析给出一阶的一个近似。它不能分辨是找到了最大值或者最小值(或者都不是)。
变分法在理论物理中非常重要:在拉格朗日力学中,以及在最小作用量原理在量子力学的应用中。变分法提供了有限元方法的数学基础,它是求解边界值问题的强力工具。它们也在材料学中研究材料平衡中大量使用。而在纯数学中的例子有,黎曼在调和函数中使用狄利克雷原理。
同样的材料可以出现在不同的标题中,例如希尔伯特空间技术,莫尔斯理论,或者辛几何。变分一词用于所有极值泛函问题。微分几何中的测地线的研究是很显然的变分性质的领域。极小曲面(肥皂泡)上也有很多研究工作,称为普拉托问题。
分析力学 是理论力学的一个分支,是对经典力学的高度数学化的表达。可以认为1788年拉格朗日发表的奠基之作《分析力学(Mécanique analytique)》是此分支的开始。
经典力学最初的表达形式由牛顿给出,大量运用几何方法和矢量作为研究工具,因此它又被称为矢量力学(有时也叫“牛顿力学”)。拉格朗日、哈密顿、雅可比等人使用广义坐标和变分法,建立了一套同矢量力学等效的力学表述方法。同矢量力学相比,分析力学的表述方法具有更大的普遍性。很多在矢量力学中极为复杂的问题,运用分析力学可以较为简便的解决。分析力学的方法可以推广到量子力学系统和复杂动力学系统中,在量子力学和非线性动力学中都有重要应用。
分析力学又分为拉格朗日力学和哈密顿力学。前者以拉格朗日量刻画力学系统,运动方程称为拉格朗日方程,后者以哈密顿量刻画力学系统,运动方程为哈密顿方程。
拉格朗日力学(英语:Lagrangian mechanics)是分析力学中的一种,于1788年由约瑟夫·拉格朗日所创立。拉格朗日力学是对经典力学的一种的新的理论表述,着重于数学解析的方法,并运用最小作用量原理,是分析力学的重要组成部分。
经典力学最初的表述形式由牛顿建立,它着重于分析位移,速度,加速度,力等矢量间的关系,又称为矢量力学。拉格朗日引入了广义坐标的概念,又运用达朗贝尔原理,求得与牛顿第二定律等价的拉格朗日方程。拉格朗日方程具有更普遍的意义,适用范围更广泛。
变分法?
中学生能理解最小作用量原理吗?
从零学分析力学(拉格朗日力学篇)
最小作用量原理与物理之美 by physixfan 作者高中时写的
此文为我高中所写,其实这个主题只要是在大学物理专业修过理论力学课程之后就可以掌握。基于本文在网上还是有一定影响力,在此对排 版上做一些改进,以变得更加美观... 个人网站:宇宙的心弦
相对论
伽利略变换?
这是你理解相对论的另一种方法 哔哩哔哩_bilibili python manim 动画, 演示洛伦兹变换, 解释尺缩钟慢和火车隧道长度问题, 作者 两颗熟李子 高二学生?
粒子物理
【硬核科普】由浅入深以十层理解带你深度解析原子以及物质的本质! (55分钟) 哔哩哔哩_bilibili 不浮夸, 提炼概括能力强, 作者id 小学科学SSR
- 物质是由不可分割的原子组成的
- 原子是由电子、质子和中子组成的
- 原子的电子轨道是量子化的
- 原子是可以被量子数描述的
- 物质是一种波
- 我们的自然界存在反物质
- 基本粒子不只是有电子、质子和中子
- 基本粒子不满足C对称、P对称和T对称
- 粒子是量子场组成的
- 基本粒子是由弦组成的
【硬核科普】以十层理解带你深度解析光的本质! 哔哩哔哩_bilibili 同上述作者 小学科学SSR
量子物理
给自己闺女写科普的 贾明子 有两个专栏
贝尔是支持爱因斯坦的, 认同隐变量理论, 于是提出贝尔不等式, 但实验结果违反了他的不等式, 说明玻尔的理解是正确的
严谨的贝尔实验, 还需要让观测者以自由意志选择观察哪个方向的自旋, 叫 "大贝尔实验"
贝尔不等式
叠加态: 一个粒子的属性 (自旋, 偏振方向, ...) 仅在测量后才能确定, 在测量前是叠加在一起的
纠缠态: 同来源的两个粒子去测量某个属性, 它们的测量结果一定相反 (否则违背能量守恒)
当测量粒子的 位置/自旋方向/偏振方向... 时, 必然要用某种手段跟粒子交互, 但这就干扰了被测粒子本身的状态, 于是我们无法得知在测量前的粒子状态
由同一来源制造出一对粒子, 必定具有相反的属性 (如两个粒子分别是向上向下自旋), 这意味测量其中一个, 那另一个粒子的状态也随之确定了
以上是物理学家公认的事实, 但是对于怎么理解这些现象, 有两种派别:
爱因斯坦的观点:
- 即使在测量前, 粒子也应该具有确定的自旋方向
- 对于纠缠的两个粒子, 也是自从分裂的那一刻起, 就已经确定好了谁向上谁向下自旋
- 只是我们受限于科学水平, 尚不知道是什么因素决定了粒子自旋, 这些不为人知的因素叫做 "隐变量"
- 光速是信息传递上限, 粒子之间不该有超光速的通信手段
玻尔的观点:
- 在测量前, 粒子不具有确定的自旋方向, 即状态是 "叠加" 的
- 在测量前讨论粒子的属性无意义
- 测量过程会迫使粒子 "坍缩" 到确定的向上或向下自旋
- 一对纠缠的粒子, 如果测量其中一个, 除了会迫使该粒子坍缩到确定状态, 还会迫使另一个粒子坍缩到相反的确定状态, 且这是瞬间完成的, 即使这俩粒子已经相距数光年之远
贝尔的贡献是, 设计出了实验, 用来判断到底谁说得对
贝尔初衷是想支持隐变量理论, 觉得实验结果一定会遵守他的贝尔不等式,
但是这些年人们反复做了许多次实验, 发现贝尔不等式都被违反了, 这说明爱因斯坦错了, 玻尔的理论是正确的
今年诺奖就是颁给三个不断完善贝尔实验, 弥补实验漏洞的物理学家
揭秘 2022 诺贝尔物理学奖:量子纠缠与贝尔不等式
EPR佯谬
什么是测量?
Quantum computing for the very curious 项目
"呈现在一种新的助记媒介中,几乎可以毫不费力地记住你读过的内容"
是个实验性的网页教程
中间隔三岔五有提问题, 按照遗忘曲线, 定期重复问
ScienceClic 简介与目录 - 哔哩哔哩
法语频道,创建于2014年,致力于物理可视化 "重温了ScienceClic的量子场论科普,我觉得大家看那个就足够了" "暴涨理论那期真的很棒"
天文和宇宙学
大部分内容都分类到了物理章节
不对啊, MOC 不应该是单分类, 可以也放在这里
科学哲学
笔记 科学究竟是什么? - 三点水