Meet in Maths 专栏简介与群表示论
title: 专栏简介与群表示论
permalink: https://zhuanlan.zhihu.com/p/22970906
author: Cyberman
author_id: 9537d5520b80eef1771e7bfef8982381
column: Meet in Maths
column_id: eleven-dimension-math
voteup: 539 赞同
created: 2016-10-15T16:17:17
updated: 2024-03-01T14:41:52
fetched: 2024-06-20T11:28:05
count: 约 16421 字
version:
tags: [代数, Cyberman, Meet-in-Maths]
url: https://zhuanlan.zhihu.com/p/22970906
-- 于 2024-06-20 重新抓取, 序言变化了, 其他没啥变化, 作者ID Chaos => Cyberman
专栏简介与群表示论
from 专栏 Meet in Maths
话题:
代数, Cyberman, Meet-in-Maths
正文:

【 Meet in Maths :由于现代数学的发展过于庞杂,本专栏在力图严谨、清晰、简洁的框架下,分享一些整理的数学笔记的心得,做一些抛砖引玉的活~(本专栏要求具备 本科数学系 的基础知识以及 大学物理 的基础知识)当然,我们最终的目标是尝试在基础数学的主要分支上做到一些前沿性的整理: 代数与数论 (代数几何+算数几何); 几何与拓扑 (几何分析+低维拓扑); 分析与方程 (调和分析+偏微分方程); 概率与统计 (随机微分几何+大模型)。如果笔者还有能力,可能会再考虑 理论物理 和 计算机 方面的一些记录。当然,一切只是一个“极大理想”。】
(具体来说,本科数学知识包括:《数学分析》、《线性代数》、《抽象代数》、《常微分方程》、《复分析》、《实分析》、《概率论》、《统计学》、《拓扑学》、《数学物理方程》)
对于 分析 、 几何 、 概率 来说,最基本的考虑对象: 基本空间 + 函数空间 (当脑回路堵塞的时候可以想想现在考虑的是哪个东西)。当有了这两者之后,最主要做的事就是 微积分 。
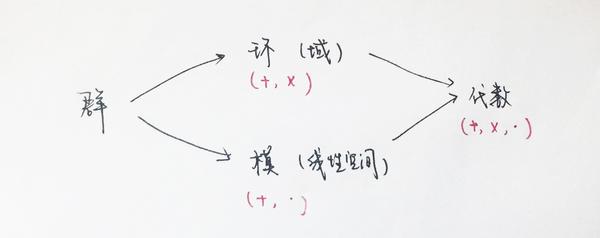
群论(Group Theory) 是现代数学尤其是代数学分支很重要的一个领域,并且也为现代数学提供了一种最基础的语言,研究群的目的是为了研究这个群的具体结构。
首先,我们先抽象的了解一下什么是群以及群是怎么来的?
一个 群(Group) 是一个比较好的代数系统,一般的定义是:如果一个非空集合上有一个二元(封闭的)运算(本质是一个映射),且满足有单位元e、结合律以及可逆性,那么这个集合称为一个群。
例如整数集Z,取加法为定义中的二元运算,即把Z中的任意两个元素a、b映射到a+b还是属于Z,并且0是单位元,a的逆显然是-a,加法运算保证了结合律。再例如n维可逆矩阵构成的集合在乘法运算下也构成一个群。
数学中有很多这样的在上述性质的二元运算下的集合,我们把这种特性抽象提取出来,于是有了群的概念。
现代数学研究群的结构一般有两种方法,并且这两种方法对应了两门不同的研究群的课程(前者是后者的基础):
把这个 "第一种方法:研究它的子群" list 项目提升到标题
第一种方法:研究它的子群
“To study a group, it is important to study its subgroups!”
第一步:导出正规子群与商群的概念
【子群】什么是一个群G的 子群(Subgroup) ?G中的子集H如果还是一个群(即在原来群的运算下封闭),那么我们称H为G的子群,记作H≤G。
【陪集】给定一个群G,我们先看看它的阶数(元素的个数)与它子群阶数的关系,这就引申出了子群H的 陪集(Coset) 的概念:对于H≤G,H的陪集可以看做群G关于H的一个划分,并且划分下每个等价类称为子群H在G中的陪集。类似于陪跑的概念,把鲍勃·迪伦及他的粉丝看成文学者构成集合的“子群”,那么陪跑的村上春树及他的粉丝就是鲍勃的一个“陪集”。并且所有等价类中的元素的势(Cardinality)相等(即可以建立一一对应关系),于是进一步有了 拉格朗日定理 :说明了 有限群 的子群的阶数(所有元素的个数)一定整除G的阶数。这个性质可以大大提高我们对G的子群的了解,例如素数阶群一定是循环群等等。
【正规子群与商群】但是光利用陪集将G进行划分还不够,我们想找个性质更好一点的子群N,使N的所有陪集构成一个群(每个陪集即等价类看成一个元素),即 商群(Quotient Group) ,记为G/N。通过运算我们知道必须让N是G的 正规子群(Normal Subgroup) ,即在G的共轭作用下不动,记为N⊴G(即每个元素去干扰这个集合,但这个集合依然不变,有点出淤泥而不染的感觉)。更进一步地,我们又可以得到关于商群的群同态三个基本定理等等。(注:同态是两个群之间的一个映射,这个映射保证了两个群关于运算的相似性,而若这个映射是双射,那么称这两个群同构,即两个群“一模一样”) -- 同构基本定理 - Wikiwand
第二步:深入研究正规子群和商群
【单群】既然有了正规子群的概念,研究到这里就足够了吗?显然还不够,因为只用定义去找正规子群是很!困!难!的!我们首先想知道G有没有非平凡的正规子群?如果有那么有多少个?一个性质是如果G没有非平凡的正规子群,即G只有{e}和G本身是G的正规子群,则称G是一个 单群(Simple Group) 。
【正规子群序列】那么如果G不是单群,即至少有一个非平凡的正规子群,可不可以考虑G的正规子群、G的正规子群的正规子群、G的......?这样就形成了一个 正规子群序列(Normal Subgroup Sequence) ,也就是{e}=Gn⊴...⊴G2⊴G1⊴G0=G,Gi+1是Gi的正规子群。(注意,Gi+2不一定是Gi的正规子群!)
【合成序列】如果G有这个正规子群序列,那么我们可不可以再进行分解,即每两个中间再插一些,分成原来基础上更细的序列,直到不能更细(也就是Gi/Gi+1为单群,且Gi≠Gi+1)?合成序列的定理告诉我们,对于 有限群 G来说答案是肯定的,也就是G的任意一个正规子群序列可以加细成为 合成序列(Composition Sequence) ,不能再加细,类比于24的因子的一个序列(1,4,24)可以加细成(1,2,4,8,24)。(任意相邻两数的商是素数)
【Jordan-Holder定理】那么问题又来了,24可以有(1,2,4,8,24)这个因子序列,也可以有(1,2,4,12,24)这个因子序列,(1,4,24)分到最后的两个因子序列的长度是不是一样,相邻两个元素的商可不可以有个一一对应?也就是G的两个合成序列{e}=Gn⊴...⊴G2⊴G1⊴G0=G与{e}=Hm⊴...⊴H2⊴H1⊴H0=G中的m是否等于n?以及{Gi/Gi+1}与{Hi/Hi+1}见是否有个一一对应? Jordan-Holder定理 告诉我们答案是肯定的。
【有限单群分类定理】至于合成序列与单群为什么这么重要,是因为在深入研究一个 有限群 G时,经常会发现 一个命题对有限群G成立当且仅当对它合成序列中的有限单群Gi/Gi+1也成立 !进而会很多数学家对有限单群进行深入研究。而有限单群分类定理是对单群进行分类研究这项巨大工程的重要产物,但由于单群分类定理的证明非常不漂亮,用了长达五千多页的文字,并且证明存在漏洞还没有完全修补完!所以暂时还不为大多数数学家所接受,因此目前也有很多人试图用更简洁的证明来将有限单群进行分类。在此我们就不深入讨论下去了。
【可解群】好了,我们再回到正规子群序列,另一个角度看它的性质(注意:不一定是合成序列)。存不存在某一个正规子群序列使得Gi/Gi+1是一个Abel群(即运算可以交换的群,又称交换群)?如果存在,我们称G为一个 可解群(Sovable Group) 。一个显然的命题是一个单群如果不是Abel群,那么它不可解,所以由一些定理可以知道,n≥5时,由于An是单群但非Abel群所以导致An是不可解的,所以Sn是不可解的。
【换位子群】但是找一个性质这么好的序列来判定G为可解群太过麻烦,我们换一种思路:反推一下,如果N是G的正规子群,那么 G/N是Abel群有没有什么等价定义 ?通过反演推算我们可以得到G的子群 换位子群G'(Commutator Subgroup) 这么一个概念,(G'还是G的正规子群)并且可以知道G/N为Abel群等价于N是G'的子群,即G'是N的一个支撑,这样可以得到 有限群 G为可解群的另一种等价定义:G可解等价于G的换位子群序列Gn⊴...⊴G2⊴G1⊴G0=G(即Gi+1是Gi的换位子群)能下降到{e},即存在n使得Gn={e}。这样大大方便了我们研究G是否可解的充要条件。
到此,《抽象代数》中研究群的子群这个主干线就告一段落。
第二种方法:群表示
注:
- 以下,
- 本文中同一个表示皆指等价的表示组成的等价类,不同的表示皆指不等价的表示。
- 什么是表示?什么是群的表示?

表示理论(Representation Theory)是代数学的一个重要的方向,现代的表示论除了研究有限群的表示,还研究结合代数的表示、李代数的表示,甚至抽象到模表示等等。
群的表示也就是研究给定的群
- 表示与作用的等价
用数学的语言来说,即先考虑群
满足:1.
如果把
反过来,一个表示(即同态映射
所以, 表示和作用是等价的 。当然,若
- 为什么研究群的表示?
再看,由于同态,所以
这种研究思路比第一种方法拓宽了许多,而且很多方法一解决得了或解决不了的问题都可以用这种方法解决,Sylow定理就是一个很好的例子。
- 什么样的群表示最值得研究?
在本文中,我们主要想研究: 有限群
然而,由Maschke定理可以知道,
它们的个数和次数满足什么样的条件,即不可约表示“长”什么样 ?
下面我们具体对群表示论的学习思路进行整理:
【一】商群——群的所有一次不可约复表示
首先,正如所有1维线性空间是不可分解的一样,所有1次群表示都是不可约的。我们想采取构造方法,先来看看一个群
【分析思路】
一个命题是,
而
【总的结论】
群
【二】群代数上的左模——群的所有不可约复表示的个数和次数
利用特殊的商群——换位子群只能研究一个群的所有1次(不可约)表示,想研究更一般的一个群的所有不可约表示,我们换一种思路,即利用一个群诱导的它的群代数的所有不可约表示(即不可约子模)来探讨群的所有不可约表示“长什么样”。
【分析思路】
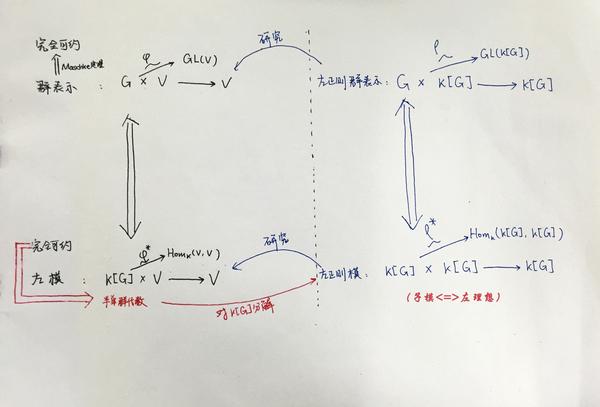
对上述主要分析思路图中的
(1)群
先给个粗糙一点的答案:群
究竟怎么个“藏法”,更一般地,我们还需要研究半单代数的 左正则 模,于是有了下一张进一步的研究思路图:
(核心:环的 左正则 模中, 子模
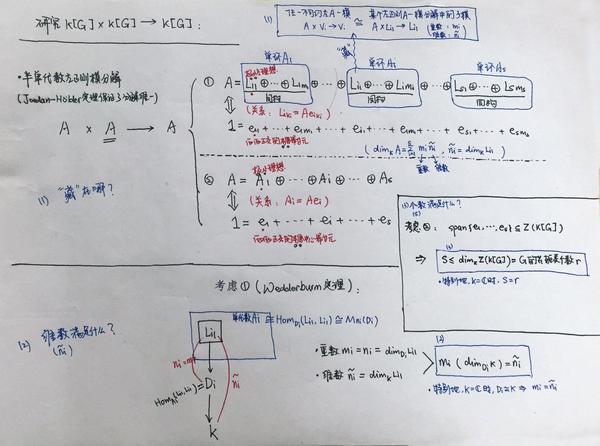
由半单代数
结论1:半单代数
因此,群代数
因此,群
(2)群
对上图直和分解中的①两边取维数得到:
(注:事实上,Wedderburm定理首先是解决了更一般的有限维半单代数的表示的结构,即它的所有不可约表示(左模)“藏”在它的左正则模中)
结论2: 当
(3)群
对上图直和分解中的②,令
结论3: 当
【总的结论】
群
设群
再设
则有群表示的同构
当
所以 左正则 表示包含了所有不可约表示的信息!
【三】表示的特征标——再论群的所有不可约复表示的次数
到现在,我们得到了关于一个群
- 群
我们引入表示的 特征标 概念:群
(1)
(2)(类函数)
(3)(线性性)
(4)(张量积)
(5)(外张量积)
(6)
(7)
(8)
(9)
有了这些准备后,我们开始对最初问题进行展开分析,即用特征标的概念来刻画一个群的表示。
【分析思路】
(1)(第一正交关系)群的两个 复 表示等价的充要条件

考虑群
于是便有了第一正交关系:
由第一正交关系,我们还可推得:群
,(
(2)(第一正交关系)群的 复 表示为不可约的充要条件
由上述的一一映射以及第一正交关系我们还可以推得:
(3)(第一正交关系)群的不可约 复 表示次数所满足的另一个条件
回到最初问题:通过大量例子,我们发现,群
(
利用模论相关知识,由于 所有代数整数构成的集合是
【总的结论】
群
进一步,回答最初问题:群
。
【四】张量积表示——再论群的所有不可约复表示的次数
继续探讨:
- 群
在范畴论中我们知道,在线性空间范畴(或更一般的模范畴)中,除了直积、直和,还有一种构造更大对象的方法——张量积。
张量积的特例是线性变换的张量积——Kronecher积的概念,其含义是两个线性空间
(1)
(2)
有了这些准备,我们开始研究表示的张量积。由于表示的直和过于平凡,其不能得到不可约表示,因此我们希望通过表示的张量积来 构造 群
【分析思路】
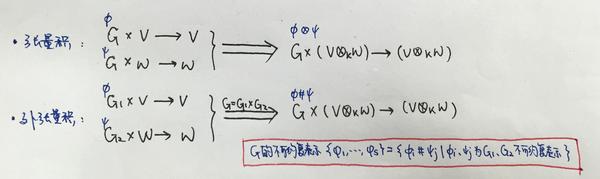
(1)(张量积)从 外部 构造
给出群
得到
并且,若
(2)(外张量积)从 内部 构造
给出群
得到
并且,当
(3)(外张量积)群的不可约 复 表示次数所满足的另一个条件
回到最初问题:通过大量例子,我们还发现:设
通过不可约 复 表示:
构造出
,其也为不可约 复 表示
再构造某个
【总的结论】
通过张量积,我们可以得到新的
进一步,回答最初问题:群
【五】诱导表示——再论群的所有不可约复表示的次数
继续探讨:
- 群
在上一章中我们通过张量积和外张量积来构造群
【分析思路】
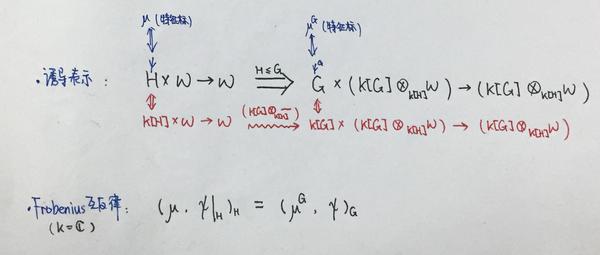
(1)(诱导表示)从 内部 构造群
设群
(2)(Frobenius互反律)群的不可约 复 表示次数所满足的另一个条件
Frobenius互反律刻画的是群
再利用这种关系可以证明出群
(注:若
【总的结论】
通过诱导表示,我们可以从
进一步,回答最初问题:群
【附】Abel群的不可约复表示
1. 特殊:循环群的不可约复表示
我们先来看看特殊的Abel群——循环群的所有不可约 复 表示长什么样。
设
其中,
2. 一般:Abel群的不可约复表示
再看看一般的Abel群的所有不可约 复 表示长什么样。
设
其中,
评论:
光能丰: 写得很好!条理很清晰! (6 🤍)
Cyberman: 谢谢! (2 🤍)
定10反5: 感觉写得很具有丘维声老爷子风格。请问阁下学习的时候用的哪本教材,授课老师为哪位呢? (5 🤍)
Cyberman: 丘老爷子😜 (2 🤍)
坐看云起时: 子群那最好强调一下,那个子集必须对原来的群的运算构成子群吧,要不然初学者会有一些误解。 (3 🤍)
Cyberman: 👌 (1 🤍)
梁骁: 看到照相两个字就知道是丘老爷子的学生了😝 (1 🤍)
SJH SHI: 怪不得
知乎用户s67n6q: 写的很好,对我很有帮助。谢谢你😊 (1 🤍)
Cyberman: 客气~
常常: 才开始自学群论,这里写的还是有很多看不懂得,还是要谢谢楼主 (1 🤍)
Cyberman: 加油!
清溪: 刚好是我正在看的书的前五章,后面的部分比较头疼 (1 🤍)
666666666661: 666 (1 🤍)
SOLOIST: 感谢分享 :) 还在学习,依然懵逼中 (1 🤍)
kasaki: 有个错误:n维矩阵不一定有逆,也不一定构成群吧
Cyberman: 好的,谢谢!
隐身人: 为什么所有的不可约表示都在正则表示中呀?只学了群论初步,能不能用线代的语言解释一下?
Cyberman -> 隐身人: 应该不能。要用到群代数和模论的知识。 (1 赞)