语言背后的代数学(八):范畴
title: 语言背后的代数学(八):范畴
url: https://zhuanlan.zhihu.com/p/35237925
author: 何幻 (30c47a685a97a71e196e87cc60e494c6)
column: 业余程序员的个人修养 (self-discipline)
voteup: 72 赞同
created: 2018-03-26 01:46:40
updated: 2018-03-26 01:46:40
fetched: 2021-09-19 05:20:00
count: 约 5530 字
version:
tags: [范畴, monad, Hask]
from 专栏 业余程序员的个人修养
话题:
范畴, monad, Hask
正文:

回顾
上文中,我们用群,拓扑空间,CPO作为例子,
来说明什么是 数学结构 ,以及数学结构是如何通过映射来保持的。
群同态保持了群结构,连续映射保持了拓扑结构,连续函数保持了完全偏序结构。
那么群结构与拓扑结构之间是否有联系呢?
我们能否建立拓扑空间与群之间的对应关系呢?
在代数拓扑中,就存在这样的例子,
人们找到了和拓扑空间相关的群论概念,例如基本群和同调群,
拓扑空间的连续映射可以导出这些群的群同态。
这就为了人们使用代数学方法研究其他数学分支,奠定了基础,
实际上,最原始的范畴论想法也是起源于此。
1. 图示法
在前一篇中我们学过了 幺半群 ,
它指的是一个集合
(1)
(2)
这两个条件除了可以用等式来表示,还可以用 图 (diagram)来表示,
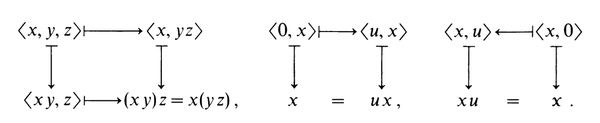
我们称以上两张图都是 可交换的 (commutative),
即,沿着不同的路径进行运算,只要起点和终点相同,则运算的结果就相同。
例如,
即,
又例,
因此,
所以,我们可以用以上两个图表,作为幺半群的定义,称为 图示法 。
另一方面,考虑在集合论中讨论映射的时候,一般都不写具体元素,还可以表示为,
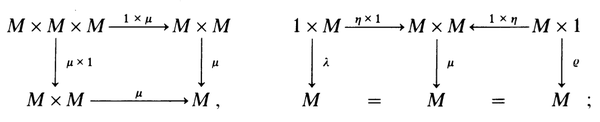
其中,
用图示法来表示幺半群,更具一般性。
2. 范畴
范畴是一个数学概念,也可以用图示法来表示。
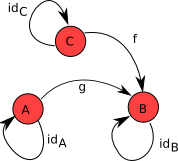
一个 范畴
对于每一个箭头
称为箭头
并且,还要满足以下几条规则,
(1)对于每一个对象
(2)箭头满足 结合律 ,对于任意的箭头
(3)箭头的集合在箭头组合运算下是 封闭的
其中,
例子:
所有的集合,以集合为对象,集合之间的映射作为箭头,构成了一个范畴,
所有的群,以群作为对象,群同态作为箭头,构成了一个范畴,
所有的拓扑空间,以拓扑空间作为对象,拓扑空间之间的连续映射为箭头,构成了一个范畴。
以上三个例子中,
范畴中的对象都是集合,箭头都是映射,这就很容易造成误解。
因为, 范畴中的对象可以不是集合,箭头也可以不是映射,
理解这一点至关重要。
例如,完全偏序
以
3. 函子
函子就是两个范畴之间的箭头。
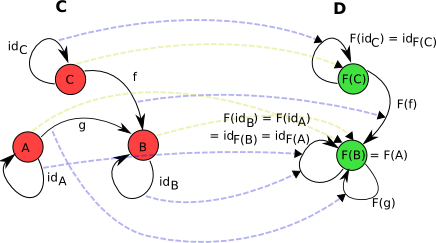
一个 函子
并且,
值得注意的是,等式左边的
等式右边的
4. 自然变换
自然变换 (natural transformation)是 一族箭头 ,
将范畴
给定两个函子
自然变换的每个 分量 (components)使下图可交换。
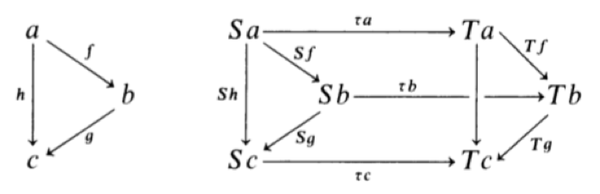
其中,
5. Monad
范畴到自身的函子,称为 自函子 (endofunctor)。
设
令
则使用
范畴
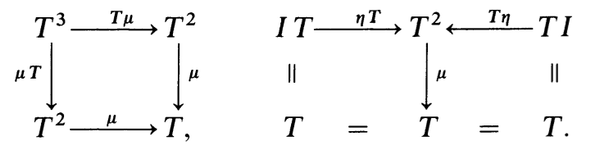
其中,
值得注意的是,Monad与幺半群的图示法是相似的,
只需要将幺半群定义中的
把单位集合
因此,我们说 Monad是自函子范畴上的一个幺半群 。
All told, a monad in X is just a monoid in the category of endofunctors of X, with product x replaced by composition of endofunctors and unit set by the identity endofunctor.
6. Hask范畴上的Monad
如果把Haskell语言中的类型作为对象,把类型之间的函数看做箭头,
则在函数复合运算下,构成了一个范畴,称为 Hask范畴 。
函子
Haskell中类型类(type class)Functor的每一个实例,定义了Hask范畴中的一个函子。
class Functor (f :: * -> *) where
fmap :: (a -> b) -> f a -> f b
fmap表示了函子作用在箭头上的结果。
作用在对象上,可以使用pure :: a -> f a来表示。
在Haskell中,一个类型要成为Functor的实例,还要满足相应的“Functor Law”,
fmap id = id
fmap (f . g) = fmap f . fmap g
可以证明,这些“Functor Law”刚好使f,fmap和pure构成了范畴论意义上的函子。
Monad
Haskell中类型类Monad的每一个实例,定义了Hask范畴中的一个Monad。
class Functor m => Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
在Haskell中,一个类型要成为Monad的实例,还要满足相应的“Monad Law”,
return a >>= k = k a
m >>= return = m
m >>= (\x -> k x >>= h) = (m >>= k) >>= h
可以证明,这些“Monad Law”刚好使m,>>=和return构成了范畴论意义上的Monad。
总结
本文介绍了范畴论相关的一些内容,
介绍了什么是 范畴 ,什么是 函子 ,什么是 自然变换 ,
这些都是理解笛卡尔闭范畴所必须的。
为了理解什么是范畴,我们列举了前一篇提到的群,拓扑空间,CPO作为例子,
还借用了Haskell中的Functor和Monad学习了Hask范畴。
下文我们将继续学习范畴论,
理解什么是笛卡尔闭范畴,以及如何用它解释简单类型
评论:
lip lee: monad那里定义的两个自然变换,Tu和uT只是两个自然变换的名字而已吗?
何幻 -> lip lee:
不是新名字,这是两个自然变换的“horizontal” composition。
Tμ中的T,可以理解为从T到T单位自然变换,因此原书中写 1 ◦ μ 可能会更好一些。
Indeed, Tμ and μT are "horizontal" composites in the sense of § II.5.
—— Categories for the Working
Mathematician
P133
lip lee -> 何幻: 原来是这样, 刚开始把T和上面的函子T当作同一个东西说不通,就在想Tμ是不是就是个名字而已,了解了,谢谢了
Max Snow: 抽象之上的抽象。。。晕了晕了 (1 赞)
知乎用户: 4. 自然变换 里面突然冒出来的a、b、c、f、g、h是啥意思
何幻 -> 知乎用户:
a,b,c,是某个范畴中的对象,f,g,h是它们之间的箭头。
Sa,Sb,Sc,是这些对象在函子S作用下的像,
Sf,Sg,Sh,是这些箭头在函子S作用下的像。 (1 赞)
Flow:
codomain不是“值域”,应该翻译成“到达域”或者“靶域”。值域是image,是codomain的一个subset,甚至完全有可能是一个proper
subset。
小火人: 不知道为啥在学集合论是就喜欢用图示助记,这种原始粗糙的理解或者就是范畴前身了OR2
慕容恪:
好文,先mark,留着慢慢读。
好专栏,已关注。