矩阵和向量组和线性方程组之间的关系是什么？ - 马同学的回答

title: 矩阵和向量组和线性方程组之间的关系是什么？ - 马同学的回答
url: https://www.zhihu.com/question/21832377/answer/202231378
author: 马同学 (matongxue)
voteup: 751 赞同
thanks: 242 感谢

create_date: 2017-07-22 23:05:58
edit_date: 2017-07-22 23:05:58
fetch_date: 2020-02-26 14:14:30
count: 约 10171 字

version: 1

话题:

数学, 线性代数, 矩阵, 高等代数

问题描述:

(无)

回答:

对于这样的线性方程组：

$\begin{cases} 2x+3y=1\\ x+y=2\end{cases}$

求解其答案的几何意义是：

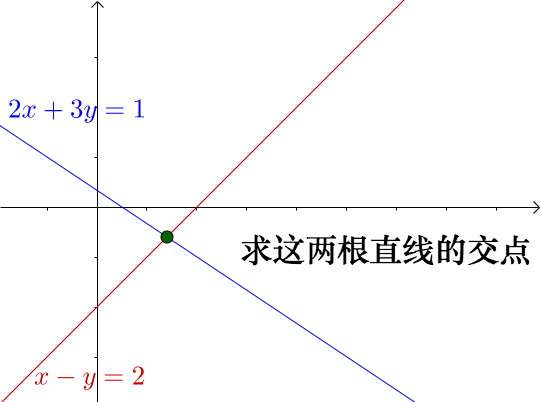
那么可以想象，解有以下三种情况：

两条直线有一个交点，方程组有一个解
两条直线共线，方程组有无数解
两条直线平行，方程组无解

如果从矩阵、向量的角度来看待这个问题，我们会得到一个全新的解题思路。

1 通过矩阵求解线性方程组

文章开头提到的线性方程组：

$\begin{cases} 2x+3y=1\\ x+y=2\end{cases}$

我们可以写成矩阵、向量的形式：

$\begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} 1 \\ 2 \end{bmatrix}$

令 $A=\begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}$ ， $\vec{x_{}}=\begin{bmatrix} x \\ y \end{bmatrix}$ ， $\vec{b_{}}=\begin{bmatrix} 1 \\ 2 \end{bmatrix}$ ，我们就得到了更一般的形式：

$A\vec{x_{}}=\vec{b_{}}$

要求解就要弄清楚这个矩阵方程的集合意义。

让我们从线性空间说起。

1.1 线性空间

先忘掉坐标系，我们从一片空白开始：

我们随便选个点作为原点，以此原点作两个单位正交的向量（因为是二维的，所以两个就够了）：

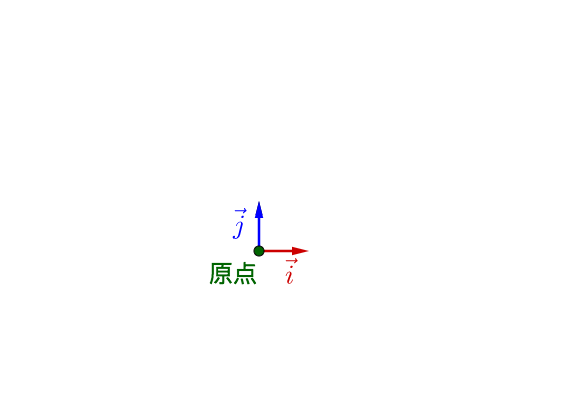
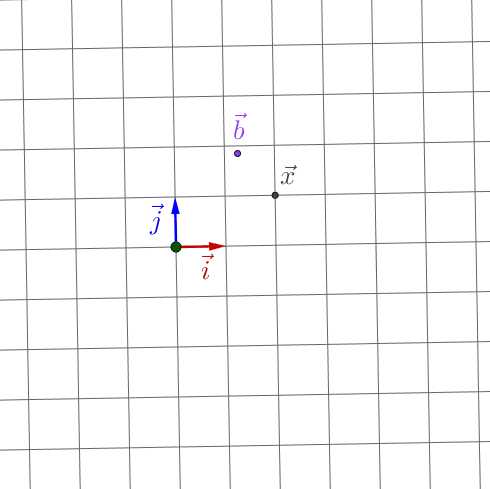
平面上的某个点，可以这样表示：

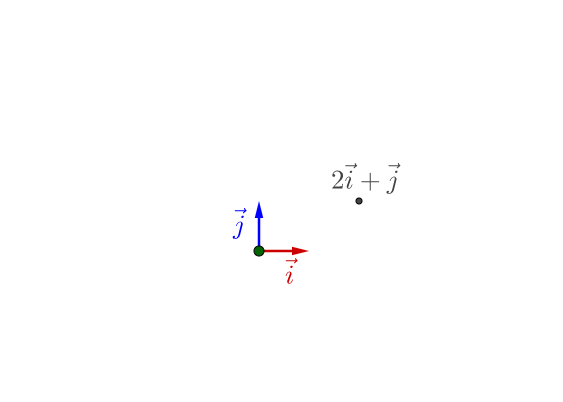
我们简化一下，这就变为了坐标的形式：

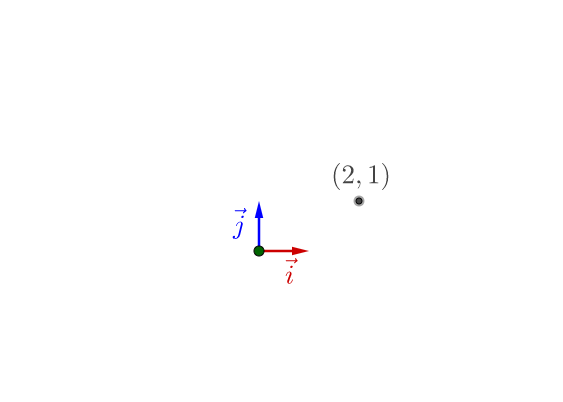
整个二维平面上的点，显然都可以通过 $a\vec{i_{}}+b\vec{j_{}},a\in \mathbb {R},b\in \mathbb {R}$ 的方式来表示。用数学的语言就是，整个二维平面是 $\vec{i_{}},\vec{j_{}}$ 所 张成的线性空间 。

为了可视化张成的线性空间，我用灰色网格来表示，网格的交点就是整数坐标：

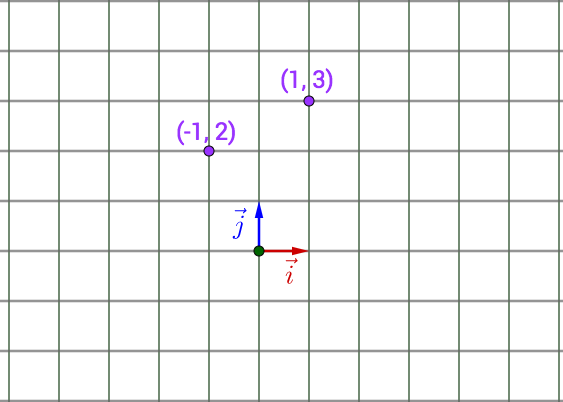
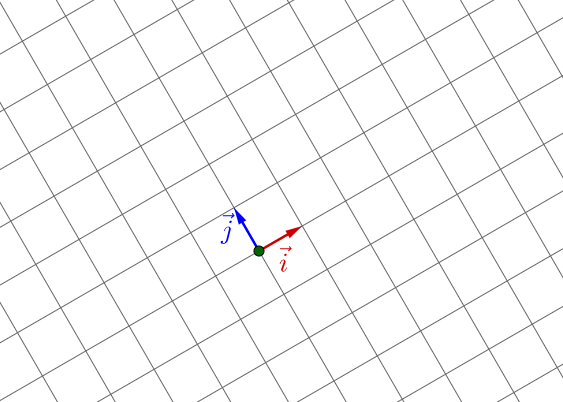
如果 $\vec{i_{}},\vec{j_{}}$ 不正交，长度也不相等，那么依然张成整个二维空间，只是网格有所不同（坐标有所不同）：

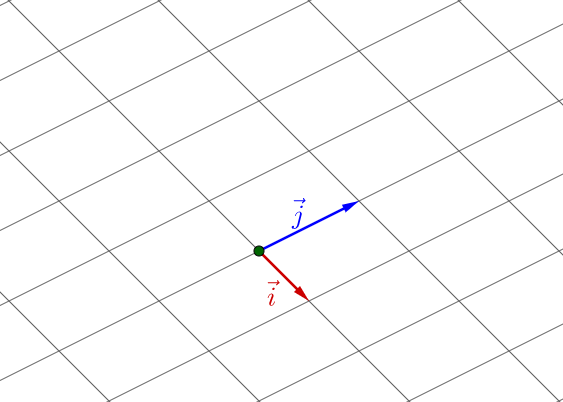
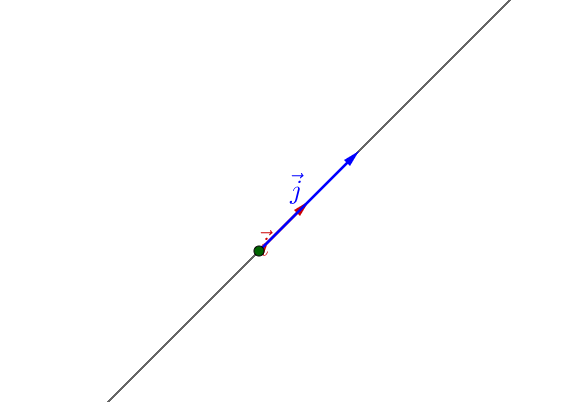
如果 $\vec{i_{}},\vec{j_{}}$ 在一条直线上，那么就只能张成一维空间：

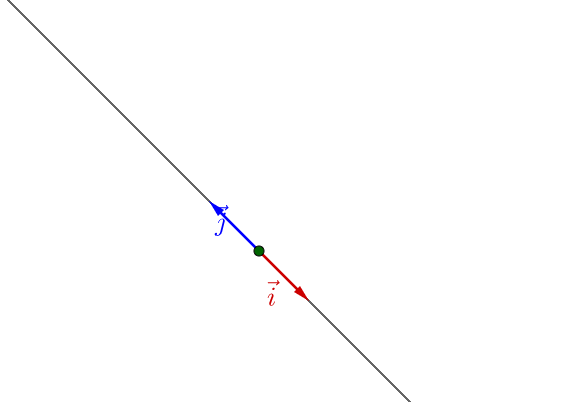
当然，如果 $\vec{i_{}},\vec{j_{}}$ 都是原点，那么就只能张成零维空间了，也就是点。

1.2 $A\vec{x_{}}$ **的几何意义**

我们把 $\vec{x_{}}$ 在单位正交基 $\vec{i_{}},\vec{j_{}}$ 下画出来：

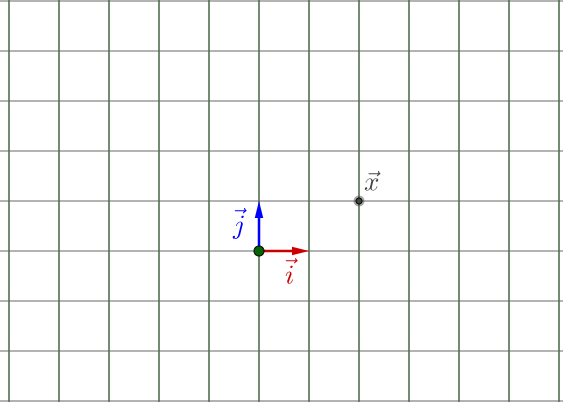
为了方便展示，我举个具体的 $A$ ，就用旋转矩阵吧（ $A=\begin{bmatrix} cos(\theta ) & -sin(\theta ) \\ sin(\theta ) & cos(\theta ) \end{bmatrix}$ ）。

那么 $A\vec{x_{}}$ 的效果是让 $\vec{x_{}}$ 发生旋转：

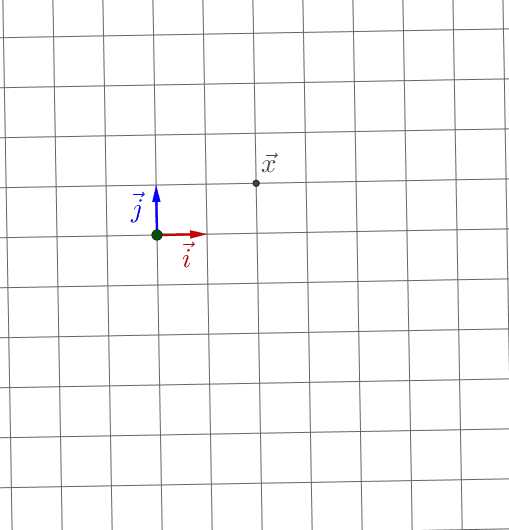
仔细观察下，变换开始时：

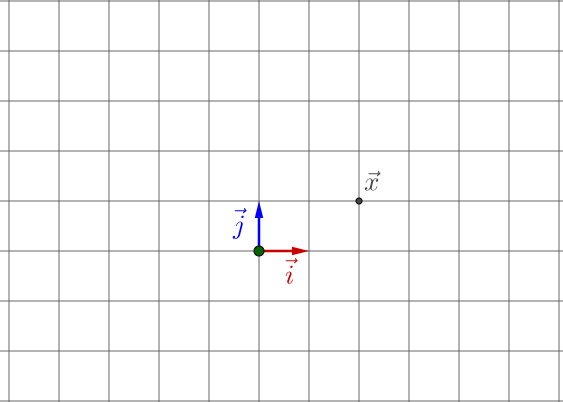
变换结束后：

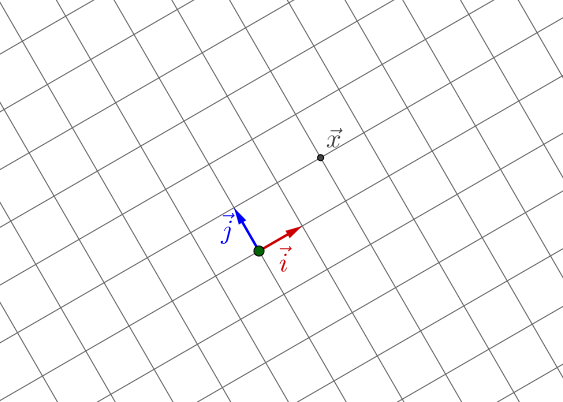
可以观察到，整个变换过程是， $\vec{x_{}}$ 以 $\vec{i_{}},\vec{j_{}}$ 为基的坐标并没有发生变换，而是 $\vec{i_{}},\vec{j_{}}$ 这两个基发生了旋转，导致 $\vec{x_{}}$ 发生了变换。

这就好比坐公交车：

我相对公交车没有移动，但因公交车移动了，我的位置还是发生了变化。

整个移动过程用公交车这个比喻来描述，就是这样的：

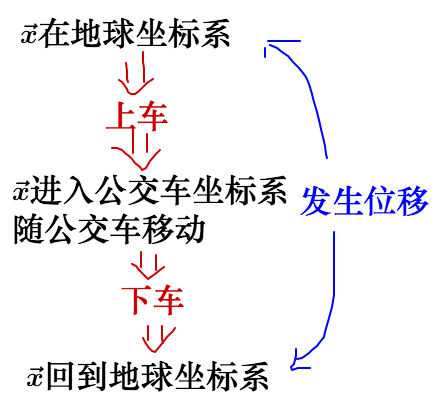
回到数学上来， $A$ 就是这辆公交车，公交车的移动取决于 $A$ 的列向量：

1.3 $A\vec{x_{}}=\vec{b_{}}$ **的几何意义**

$A\vec{x_{}}=\vec{b_{}}$ 就是说，通过 $A$ 让 $\vec{x_{}}$ 运动到 $\vec{b_{}}$ ：

借用公交车的比喻，就是在 $\vec{x_{}}$ 上车，通过公交车到达了 $\vec{b_{}}$ 。

1.4 矩阵的秩与解

这个公交车有点古怪，并非某个点上车都能到达 $\vec{b_{}}$ ，我们的任务就是找到那些可以到达 $\vec{b_{}}$ 的 $\vec{x_{}}$ 。

这就需要研究这个公交车的站牌了：

从数学上说，公交车的站牌是由 $A$ 的列空间决定的，读懂了列空间就读懂了站牌。

1.4.1 满秩

比如，旋转矩阵 $A=\begin{bmatrix} cos(\theta ) & -sin(\theta ) \\ sin(\theta ) & cos(\theta ) \end{bmatrix}$ 的列空间是二维的：

即整个二维空间上的点都在这个公交车 $A$ 的行驶范围内，那么：

并且我们还可以观察到，只有唯一一个点上车才可以到达 $\vec{b_{}}$ ：

列空间的维度实际上就是矩阵的秩（参看这个回答），所以我们得到第一个数学结论，满秩的矩阵，有唯一的解。

1.4.2 不满秩

再比如，这个矩阵 $A=\begin{bmatrix} 1 & 2 \\ 1 & 2 \end{bmatrix}$ 的列空间是一维的：

那么，假如：

这也就是无解的意思。

可以观察出来， $\begin{bmatrix} \vec{i_{}} & \vec{j_{}} \end{bmatrix}$ 的秩一定小于 $\begin{bmatrix} \vec{i_{}} & \vec{j_{}} & \vec{b_{}} \end{bmatrix}$ ，那么可以得到第二个数学结论， $\begin{bmatrix} \vec{i_{}} & \vec{j_{}} \end{bmatrix}$ 的秩 < $\begin{bmatrix} \vec{i_{}} & \vec{j_{}} & \vec{b_{}} \end{bmatrix}$ 的秩，那么无解。

如果 $\vec{b_{}}$ 在 $A$ 的列空间中，那么：

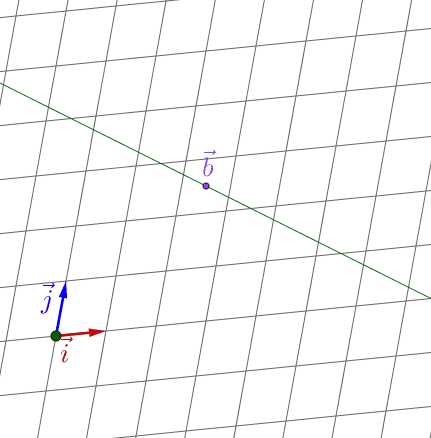
整条绿色线段上的点都会到达 $\vec{b_{}}$ 点（多一句嘴， $\vec{b_{}}$ 不一定会经过 $A$ 到达 $\vec{b_{}}$ 点），这就是有无数个解。

这个可以直观去想象，空间由二维压缩到一维，那么必然有无数多个点被压缩到同一个点上去。

至此得到第三个数学结论： $\begin{bmatrix} \vec{i_{}} & \vec{j_{}} \end{bmatrix}$ 的秩 = $\begin{bmatrix} \vec{i_{}} & \vec{j_{}} & \vec{b_{}} \end{bmatrix}$ 的秩，并且不满秩，那么有无数多个解。

1.5 小结

我们得到三个数学结论：

满秩的矩阵，有唯一的解
$\begin{bmatrix} \vec{i_{}} & \vec{j_{}} \end{bmatrix}$ 的秩 < $\begin{bmatrix} \vec{i_{}} & \vec{j_{}} & \vec{b_{}} \end{bmatrix}$ 的秩，无解
$\begin{bmatrix} \vec{i_{}} & \vec{j_{}} \end{bmatrix}$ 的秩 = $\begin{bmatrix} \vec{i_{}} & \vec{j_{}} & \vec{b_{}} \end{bmatrix}$ 的秩，无数解

经过我们上面的分析，应该还是挺直观的吧。

继续推下去很容易得到解的结构、零空间、解空间这些概念，这里就不推下去了，抛砖引玉，希望大家集思广益。

Johnny:
请问马同学，或其它同学，像3d 游戏里面的标架变换，每个子物体模型都有自己的建模标架，同时很多子模型同时又可以加入一个世界标架展示出来，标架与标架之间，与世界标架之间可能存在旋转角度不同，当然也可以搞扭曲，

那问题是，如果我已经知道了 2个不同的标架（3D欧氏空间每个标架3个列向量），如可求在这两个标架之间转换的矩阵呢？

　　
马同学回复 Johnny:
可以的，请搜索过渡矩阵 (1 赞)

小萨:
马老师，太精彩辣！给线性代数汇总成专栏可好？方便大家系列查阅，灰常感谢！

　　
马同学回复小萨:
在我的公众号里面有专栏

「已注销」:
真·从一片空白开始 (1 赞)

from: https://www.zhihu.com/question/21832377/answer/202231378

矩阵和向量组和线性方程组之间的关系是什么？ - 马同学的回答

话题:

问题描述:

回答:

评论: