title: Mathematica入坑指南 | AyanamistsBlog
category: default
tags:
- ayanamists.xyz
created_at: 2021-06-12 11:25:15
original_url: https://ayanamists.xyz/2020/10/03/2020-10-03-mma/?utm_source=cn.ticktick.task&utm_medium=social&utm_oi=27122571673600Mathematica入坑指南 | AyanamistsBlog
2020-10-03 - 2021-05-11
ayanamists
在计算机里寻求符号计算是不是搞错了什么?
计算机系的学生,大多都是明白计算机是如何做数值计算的。
比如说,你让一台x86计算机算0xff+0xff00等于多少,可以写成这样的汇编:
mov eax, 0xff ;把0xff这个数放到eax寄存器里
add eax, 0xff00 ;把eax寄存器里的数加上0xff00
至于小数,可以用浮点数去算,这些东西都能在硬件上实现。事实上,我们也写过一个简单的CPU,大概知道这些东西在电路上是什么样的。
可是,很多计算机系的学生,也不明白计算机是如何进行符号计算的。比如说,我要算以下的微分式:
这种运算是如何让计算机做的呢?请自行阅读《计算机程序的构造与解释》,这里不再赘述。我们今天的重点是,如何用mathematica来算这些东西。
通向可用的mathematica之路
mathematica是商业软件,学生版要400多元。大家可能不想出这些钱,毕竟美国公司嘛,薅点羊毛也没什么。(注意:如果要进行商业、学术使用,请使用正版软件,否则后果自负。) 想不花钱用,主要有两个手段:
- 官方免费版,我用的是这个,即wolframscript或者说wolframEngine
- 破解版,请参考 https://tiebamma.github.io/InstallTutorial/
wolframscript和mathematica有啥区别呢?主要的区别在【用户界面】上。wolframscript就是一个解释器的REPL,和python、scheme的使用方法没有太大区别。而mathematica则是一个GUI软件,是【笔记本】形式的,每一行代码都是【一个块】,可以单独执行。
说到这里,读者应该明白了,wolframscript就是给我们这些程序员用的,mathematica是给非程序员用的。当然也不用划得这么清楚,我的建议是可以都体验一下,然后再决定用哪个。
这里还要提醒一点,wolframscript会出现玄学的下载问题,如果不在linux下工作或者没有科学上网的手段,能不能安装上纯看运气~
Wolfram Language
Wolfram Language的语法
mathematica是Wolfram Language的前端,在mathematica中写下的代码本质上是Wolfram Language代码。
在Wolfram Language里,一切操作都可以似乎都通过『函数』来完成。它『调用函数』的语法似乎也很简单:
Func[arg1, arg2, ..., argn]
比如说,加法可以这样去算:
Plus[1, 2]
>>> 3
乘法可以这样去算:
Times[1, 2]
>>> 2
读者也许会惊呼,这不就是伟大的scheme lisp吗?
(+ 1 2) ;-> 3
(* 1 2) ;-> 2
可惜,这并不是,或者说不完全是伟大的scheme.
首先,所有的Wolfram Language代码都会被解析成『M-表达式』,这可以用FullForm得到验证:
FullForm[a + b - c]
>>> Plus[a, b, Times[-1, c]]
而这个『M-表达式』正是『S-表达式』的变种,简单来说,
(a b c d e f ...)
和
a[b, c, d, e, f, ...]
是等价的。
不过更有趣的是,Wolfram Language中的Apply函数的作用,是:
Apply[ a[b, c, d ...], a' ]
= a'[b, c, d ...]
比如说:
Apply[Plus, [a, b, c]]
>>> a + b + c
这里的{a, b, c}实际上是List[a, b, c]:
FullForm[{a, b, c}]
>>> List[a, b, c]
那么,Wolfram Language 和 scheme 到底有什么不同呢?这要从它的求值规则说起。
Wolfram Language的求值规则
在讨论 Wolfram Language 的求值规则之前,我们首先要搞清楚 scheme 的求值规则。scheme的求值规则简单来说和

这三条规则揭示了一个重要事实:
- 求值时要进行『深度优先搜索』,即对于表达式
然而,这些求值规则没有解释清楚这样一个事实,那就是当
这看似应该求出来
在scheme中,一个『自由变量』被求值,会导致错误的发生,而在Wolfram Language中,一个『自由变量』的值就是其本身:
Function[{x}, x[a]][Function[{x}, x]]
>>> a
不仅一个『自由变量』的值就是其本身,任何『无法被求值的M表达式』,值都是其本身。更本质地说,『不能被求值』才是M表达式的常态,『能被求值』是因为预定义了『规约规则』。
而如何定义『规约规则』呢?Wolfram Language 中提供了Set。Set可以写作=,它定义了Set[a, b]中a要被规约成b。
显然我们需要一些表达M表达式的方法来定义Set[a, b]中的a,比如说,我们要吧factor[10]改写成10 * factor[9],但我们不想定义factor[1.1]如何改写。Wolfram Language 把这些东西叫做Pattern,比如说:_ 可以匹配一切M表达式,这可以用MatchQ来检查:
MatchQ[{1231, 231, Plus[a, b], 1}, _]
>>> True
这样一来我们就理解了在wolfram language中,『函数定义』为什么是那个样子:
factor[x_Integer] := x * factor[x - 1]
factor[0] := 1
这里的:=是SetDelayed的意思,它会阻止即时地把『绑定变量』进行求值,如果用Set则会造成一些令人啼笑皆非的问题:
x = 10;
f[x_] = x;
f[1]
>>> 10
如何评价Wolfram Language的设计
wolfram language为什么要这么设计呢?我想,Church老先生在1932年那篇提出

简单来说,我们使用的数学表达式常常含有大量的自由变量,如果都把它们绑定上会违反数学家的爱好(是不是会变得难用我觉得是一个可以继续探讨的问题),所以Wolfram Language索性把所有的东西都当成是一种『Primitive Value』,只有需要规约的时候才去进行规约。这样一来,『含有参数的微分/积分』、『纯粹的表达式化简』都得到了简化:
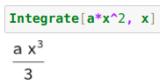
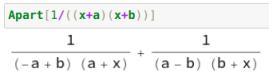
然而,这样的设计也埋下了大量隐患。如果把所有的程序看作集合
对scheme来说,这三个集合的关系大概是这样的:
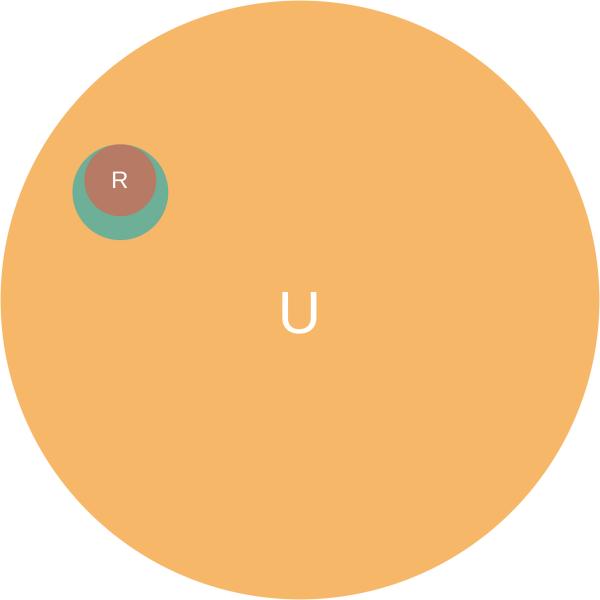
而对Wolfram Language来说,这三个集合的关系可能是这样的:
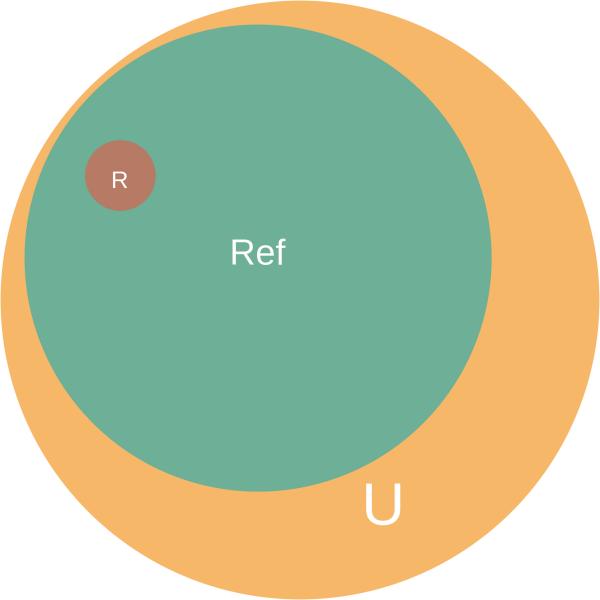
这是因为,很多在scheme中会产生运行时错误的写法,在Wolfram Language中是不会产生运行时错误的:
- 少写了参数
- 多写了参数
- 写错了绑定名
- 引用了一个未定义的绑定
所以,Wolfram Language的这些设计使得排错变得困难,很多时候都会出现极为古怪的输出(因为该求值的东西没有进行求值,继续进行计算很可能得到古怪输出)。
Post author: ayanamists
Post link: http://example.com/2020/10/03/2020-10-03-mma/
Copyright Notice: All articles in this blog are licensed under unless stating additionally.
原网址: 访问
创建时间: 2021-06-12 11:25:15
目录: default
标签: ayanamists.xyz