顺滑地进入群论 (Ep.2) ——U(1), SO(2), SO(3), SU(2)

我们首先考虑的第一个例子非常直观. 对于一个向量来说，我们有一个二维旋转操作，它可以被写为一个 的矩阵，像这样： 这个矩阵可以将一个二维向量绕着原点旋转 角度.

除此之外，还有镜像翻转的操作：

以上这些操作，再加上矩阵的乘法，我们就构建了一个群1. 以上的这些操作可以归结为 “所有保持任意向量长度不变” 的操作. 但进一步想想，在我们不知道上面这三个变换长什么样的时候，我们要如何判断这种变换的性质呢？我们下面用一种比较抽象的方法来分析一下：

假如我们考虑的向量是 ， 在进行了这样一个操作 之后，我们得到一个新的向量 要求向量操作前后的长度不变，就是要让它的内积不变，即 代入 ，我们发现

也就是说，要让向量的长度保持不变，一个操作必须满足条件 所有满足这个条件的操作组成了一个群，叫做 ，字母"O"取自"正交 (orthogonal)"的首字母.

有时候，我们并不关心 中所有的元素，而只关心 二维旋转. 一个旋转的特殊之处在于， 它不仅保证了这个线性空间中所有向量的长度不变，还保证了空间的“方向”不变. 形象一点来说就是：旋转操作不会让向量左侧的点跑到右侧去，反之亦然. 所以我们要做的就是去掉 中那些翻转了空间取向的操作2.

在数学上，要做到这一点很简单，只需要对 取行列式，满足 的操作就是我们期望的旋转操作.

那么我们总结一下，一个二维旋转 就是满足以下条件的操作： 所有满足 的操作组成了一个特殊的 群，我们就叫它 ，字母"S"取自"特殊 (special)"的首字母.

为了描述二维旋转，除了使用向量外，我们还可以使用一个模长为 的单位复数3 ，满足 为了更直观一些，我们可以把一个单位复数写为 我们将类似式 的理解搬过来，可以发现

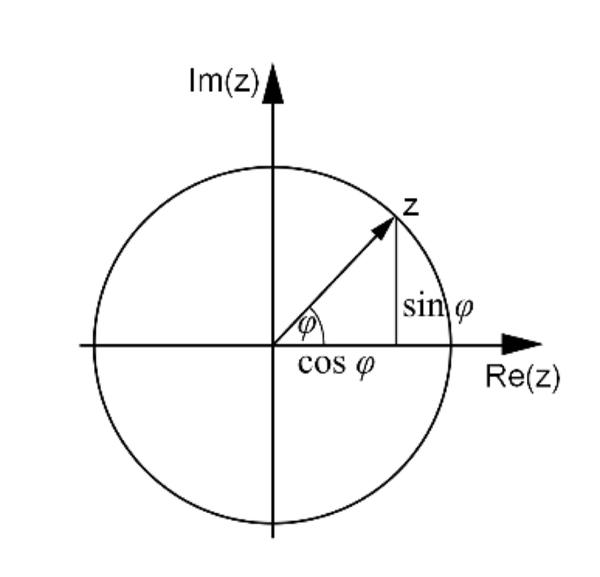
图1: 复平面上的单位圆

因此复数 的作用和旋转矩阵 是类似的. 但需要注意的是， 复数的幅角 和 中的旋转角 并不是同一个参量 4，我们会在后面讨论这个问题.

为了更清楚地将复数表示和前文 的表示联系起来，我们可以这样理解：定义 然后自然就有以下关系： 可以看到，我们通过将复数 映射到一个实矩阵上，仍然保持了其数学结构. 同时，我们还发现：

所以复数 和旋转矩阵 具有相同的作用，都可以表示一个二维旋转，旋转角满足
这个单位复数表示的操作，我们记作 . 可以看到，为了描述一个二维旋转，它需要满足的条件是 所有满足 的操作组成了一个 群，字母"U"取自"幺正 (unitary)"的首字母. 从上面的分析也可以看到， 和 都描述了二维旋转操作，因此这两个群之间存在同构 (isomorphism).

群是三维的旋转群，它的定义和 非常类似，只是多了一个维度，在这里就不赘述了. 值得注意的是，一个二维旋转只需要一个旋转中心，而一个三维旋转需要三条旋转轴才可以确定，围绕三条旋转轴的旋转矩阵分别是

和二维旋转类似，我们希望用一个“高维复数”来表示三维旋转. 在二维情形中，由于旋转只需要由一个旋转中心确定，所以我们使用的复数只有一个虚部 . 在三维情形中，由于存在三个旋转自由度 (三条旋转轴)，我们必须使用具有三个虚部的数学结构描述一个旋转，这个结构就是所谓的四元数： 其中 满足 和复数类似，一个单位四元数满足 由此可以看到，单位四元数及普通的复数乘法构成了一个群.

类似地，我们还可以用矩阵和矩阵乘法等价地表述这个群. 由条件 [5]可以进行下面这样的定义： 于是就有 也就是说，单位四元数可以映射到 矩阵上，同样满足条件 这样，我们便定义了 群.

直觉上， 和 的关系就像 和 一样自然，但遗憾的是，实际上并不是这样的. 我们在二维旋转的情形中，用复数 表示了相同的旋转 ，并且指出了 . 但在三维旋转的情形中，它们就不相等了. 这就是为什么我在前文中强调了 和 是两个不同的参数.

为了说明 和 的关系，我们用一个具体的例子来说明：

首先，我们考虑一个用四元数表示的向量 代入 中的定义，有 现在我们尝试把这个向量绕着 轴旋转一个角度 ，我们只需要将 作用在它上面就可以了. 用四元数可以表示为 值得注意的是，四元数的乘法和矩阵的乘法并不是等价的，所以将 作用在向量 上的时候，并不是直接将它们相乘，而是[6] 经过计算，得到 用四元数表示则为 可以看到， 使向量 绕 轴旋转了 的角度[7]. 从这里可以看出， 中的角度与 中的角度并不是等价的角度.

为了更清晰地说明这两个群的关系，我们将一个任意的单位四元数写为 其中 是一个单位四元数，且 . 这里很容易可以验证 从式 的结果可以看出，我们实际是将向量 旋转了 的角度，而不是 . 所以 可以写为 这个结果告诉我们，四元数表示的旋转 ( ) 和矩阵表示的三维旋转 ( ) 之间的映射并非是单射，比如： 而这两个结果都对应着一个角度 的三维旋转. 因此，我们说 是 的 二重覆盖 (double cover).

下期传送门