from 专栏 ZCC的代数随笔

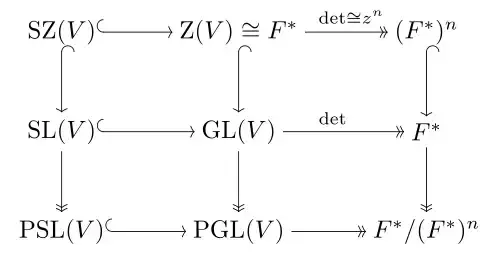
本文所需要的线性代数基础不再赘述, 这方面[1]是一本较好的教材. 给定域 上的线性空间 , 上所有线性变换的集合一般记为 , 不难证明 关于线性变换的加法和乘法构成一个(含幺)环. 这个系列并不关注 作为环有怎样的结构, 而是着重于用相对初等的手段研究 的单位群及其子群、商群的某些性质. -- #comment "Endomorphism"（内射）的缩写

的单位群 称为线性空间 上的 一般线性群 (general linear group); 如果 , 也记为 . 的子群称为 上的线性群. 相当于是 的"自同构群".

我们只讨论 是有限维线性空间的情况. 由于在有限维的情况下, 中的元素都可以(通过给定的一组基)和 上的 阶方阵建立一一对应, 因此实际上比起考虑线性群, 我们不妨考虑更具体的 矩阵群. 上的 阶可逆方阵的集合关于矩阵乘法构成群, 这个群和 同构, 在不引起歧义的情况下仍记为 .

一些常见的线性群——

• (1). 特殊线性群 (special linear group) : 所有行列式为 ( 中的幺元)的方阵(或说是线性变换也行)构成的集合是 的子群, 称为(域 上的) 维特殊线性群, 记为 .
• (2). 正交群(orthogonal group): 维欧氏空间 上的所有正交变换构成的集合是 的子群, 称为 维正交群, 记为 . 中所有行列式为 的元素构成 的子群, 称为 维特殊正交群, 记为 . 正交群及其子群具有鲜明的几何性质.
• (3). 酉群(unitary group): 维酉空间 上所有酉变换构成的集合是 的子群, 称为 维酉群, 记为 ; 类似前面的定义, 也有特殊酉群 .
• (4). 辛群(symplectic group): 比较复杂且本系列不会涉及, 有兴趣请参考链接中的内容.

上面定义的线性群都能在一般的线性空间观点下推广.

的中心商群 (central quotient, 即该群对中心的商群) 称为 上一般 射影线性群 (projective linear group, 题图亦来源于该网站), 记为 ; 如果 , 也记为 . 类似地可以定义特殊射影线性群 , 有时也将 简记为 , 其中 是一个域.

为什么把这样的商群叫做射影线性群? 它实际上是射影空间中射影变换的集合.

. 其中 同构于(从而可以看作是)域 的单位群.

题图中的一个短正合列.

构造 到 的满同态 , 使得 . 并由此证明 是单群.

参考[2].

是(同构意义下唯一的)168阶单群.

Fano平面的自同构群. 以后我们将证明除了极个别情况之外, 一般都是单群. 比如 是最小的单群.

[1]: [俄]科斯特利金 著, 牛凤文 译.代数学引论. 第二卷, 线性代数: 第三版[M].高等教育出版社:北京,2008.
[2]: [俄]科斯特利金 著, 郭文彬 译.代数学引论. 第三卷, 基本结构: 第三版[M].高等教育出版社:北京,2007:39.

title: 线性群的初等讨论 2 特殊线性群的基本性质
permalink: https://zhuanlan.zhihu.com/p/119162854
author: ZCC
author_id: 6905106fcab33fc4f75aadffdd0fb07c
column: ZCC的代数随笔
column_id: c_1147084764438691840
voteup: 40 赞同
created: 2020-03-28T17:49:24
updated: 2020-10-13T18:52:33
fetched: 2024-06-09T18:23:26
count: 约 3212 字
version:
tags: [代数, 线性代数, 群论, ZCC, ZCC的代数随笔]
url: https://zhuanlan.zhihu.com/p/119162854

from 专栏 ZCC的代数随笔

前一节内容传送: 线性群性质的初等讨论(1): 相关定义.

本文主要讨论特殊线性群 的性质, 其中 是给定的域. 为了方便叙述, 我们先确定几个记号.

下面的矩阵记号都是在 上 阶方阵的前提下给出的, 和 分别是 中幺元和零元.

• 表示第 行第 列是 , 其他地方都是 的方阵.
• , 即对角矩阵( ).
• .
• , 即单位矩阵.
• , 是一类初等矩阵( ).
• .

上面几种方阵的形式建议读者写一写. 我们指出:

对任意 , 存在唯一的 , 使得 , 其中 .

这是上节练习1.4的一个直接结果.

设 , 则 .

证明的关键在于理解这类初等矩阵对应的行/列变换, 我们只证明 的情况.
注意到
> 于是 中所有形如 的元素都在 中( ).
接下来不妨设 (思考: 为什么能够这么设?)则
> 从而 , 而反过来显然有 , 因此
> 至于 的情况留给读者证明, 或参考GTM2111

1

, 其中也有定理2.1的证明.

将 中的任意两个元素 按定理2.1中分解为 , 则换位子 .

只需要证明

接下来我们证明:

除当 , 以外, 就是 的换位子群.

接下来不妨用 表示 的换位子群, 并设.
由引理2.3, 显然有 .
容易得到 , 利用该式容易证明
若 , , 则存在 使得 且
> 若 , 则
> 这样我们就能得到
除当 , 以外, 存在 , 使得 .
注意到 是 的正规子群, 因而对任意 , ,都有
> 其中 .
进一步我们得到
( )
( )
从而 , 从而由引理2.2
> 综上定理2.4证毕.

证明 总是 的特征子群, 并验证当 , 时, 𝟚 不是 𝟚 的换位子群.

换位子群自然是特征子群, 只需要考虑那个例外情况即可. 事实上,
𝟚𝟚
但我们知道对称群的换位子群是相应的交错群.

除有限的几种情况外, 的换位子群都等于自身, 并说明例外情况有哪些. 从而推出 和 都不是可解群.

实际上定理2.4以及基本处理好了这个问题.
这个题目本身也是很有趣的, 但限于篇幅只能留作练习. 另外尽管 和 都不是可解群, 但它们也不是单群, 见[2]. 另外基于该题能给出一个换位子群中不全是换位子的例子: 不是 的换位子.

本文的讨论就到这里, 接下来的几篇文章仍然围绕特殊线性群, 包括特殊线性群的自同构群、证明射影特殊线性群是单群等等, 之后再基于特殊线性群的讨论来研究一般线性群.

[1]: Serge Lang.Algebra(Revised Third Edition)[M].Spriger-Verlag:New York,2002:541.
[2]: 寨森Lambda-CDM: 一些典型群

王立伟: 普通对角矩阵不能和任意矩阵可换。

ZCC: 当时脑抽了qwq谢谢指出

王立伟: 你太客气了，我受益颇丰，当谢你才对。

雷古鲁斯: 那lemma2.3是不是不成立

title: 线性群的初等讨论 3 更进一步 - 知乎
permalink: https://zhuanlan.zhihu.com/p/120761469
author: ZCC
author_id: 6905106fcab33fc4f75aadffdd0fb07c
column: ZCC的代数随笔
column_id: c_1147084764438691840
voteup: 16 赞同
created: 2020-03-30T16:14:33
updated: 2020-03-30T22:53:54
fetched: 2024-06-09T18:23:33
count: 约 1977 字
version:
tags: [代数, 高等代数, 群论, ZCC, ZCC的代数随笔]
url: https://zhuanlan.zhihu.com/p/120761469

from 专栏 ZCC的代数随笔

前一节内容传送: 线性群性质的初等讨论(2): 特殊线性群的基本性质

本节主要叙述一般线性群和特殊线性群的进一步结果. 我们首先有一个显然的引理:

设 是域 的单位群, 是 中 次单位根的集合, 则

• (1). 是 的中心.
• (2). 是 的中心.

接下来是出本节的核心定理:

除了 , 外, 如果 的子群 在 下不变(即任意 , 都有 ), 那么命题

• (1). * (2).
  至少有一个成立.

定理3.2的证明相当复杂, 我们这里仅叙述一下华罗庚使用矩阵论方法的大致证明思路, 具体证明参看[1].
首先引入一个叫做平延(transvection)的概念: 称一个矩阵 是平延, 若 是幂零矩阵. 平延是处理线性群问题中常常用到的一类对象(这并不是最标准的定义).
借助这个概念可以证明两个(著名的)结果: 所有的平延生成 , 同时构成 的一个共轭类(代表元是一个初等矩阵).
很容易证明: 若 包含一个平延, 则 包含 .
接下来可以通过反证法证明该定理: (1)不成立, 那么存在 和 使得 , 但这里不妨设 ; 由于 在 下不变, 因此换位子 , 基于这个式子通过 复杂的分类讨论和矩阵运算 可以得到 必然包含一个平延, 从而矛盾.

基于定理3.2我们可以轻而易举地推出一系列有关一般线性群和特殊线性群的命题. 注意: 接下来的讨论不考虑 和 , 的情况.

首先我们能够刻画特殊线性群的正规子群.

的真子群 是正规子群当且仅当 是 的子群.

显然 是 的在 下不变的子群, 又有 是 的真子群, 因而
> 反过来, 由于 是 的特征子群且是交换群, 因而 的子群都是正规子群从而是 的正规子群.

是单群.

是单群.

在定理3.3中我们实际上也证明了 是 的极大正规子群, 因此
> 自然是单群.

现在我们给出了除有限交错群外另一类有限单群, 对有限域 和 , 属于一类李型单群[2].

最后留下几个问题作为练习好了.

求 的正规子群.

结合练习1.4和定理3.3.

当 , 时定理3.2-3.4不再成立, 请读者计算说明.

下一节将讨论一般线性群和特殊线性群的自同构群.

[1]: 华罗庚, 万哲先.典型群[M].上海科学技术出版社:上海,1963:64-69,189-191.

ping: SL（2，p）的极大子群有明确的结构吗？

from: https://api.zhihu.com/articles/120761469

title: 线性群的初等讨论 4 线性群的自同构 - 知乎
permalink: https://zhuanlan.zhihu.com/p/127118421
author: ZCC
author_id: 6905106fcab33fc4f75aadffdd0fb07c
column: ZCC的代数随笔
column_id: c_1147084764438691840
voteup: 28 赞同
created: 2020-04-09T18:14:02
updated: 2020-04-10T13:41:44
fetched: 2024-06-09T18:23:37
count: 约 2846 字
version:
tags: [群论, 抽象代数, 代数, ZCC, ZCC的代数随笔]
url: https://zhuanlan.zhihu.com/p/127118421

from 专栏 ZCC的代数随笔

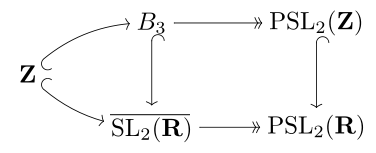
接下来我们的目的是求 的自同构群. 这个问题相当于解一个函数方程

当然 时就是求 的自同构; 但如果 , 这个方程的解就很多样了, 我们可以找到很多比较熟悉的对象充当它的解, 为方便计, 接下来将 和 简记为 和 .

自同构的例子(读者自行验证):

• (1).(内自同构)相似变换 (2).(两个反自同构复合)转置和取逆复合 (3).(诱导自同构)设域 有自同构 , 它诱导 上的自同构
  上面涉及的记号接下来会用到.

从前面的讨论中可以看出, 当 时线性群的某些结论会出现例外情况, 而当 时结论在本质上与线性群的性质无关, 因此我们接下来的讨论中主要考虑 的情况.

先前谈论线性群的性质时, 平延起到了良好的作用; 而求线性群的自同构, 对合 (involution)是一个相当好的对象. 在[1]中正是基于对合给出了 的所有自同构, 但由于证明本身和为证明所做的铺垫相当长(长达46页而且分为了三个部分讨论), 在本文就不再加以叙述, 仅给出结论作为引理.

设 , 任取 , 则存在 和 , 使得下面两个条件之一成立:

• (1). * (2).
  其中" "表示映射的复合(从左到右).

基于这个引理我们不难找到 的自同构.

设 , 任取 , 则存在 和 的自同态 使得

注意这里 按照引理4.2中的条件自然延拓到了 上(即若 , 则 , 情况(2)类似处理).

证明需要用到之前[2]的一些结果. 由定理2.4和练习2.5, 在 上的限制就是 的自同构, 即 , 再按照引理4.2中的条件自然延拓到 上得到 的自同构 .
注意这时不一定有 , 但我们考虑自同构 却有 .
由定理2.1, 只需考虑 在 下的像.
由引理4.2, 存在 的自同构 使得 , 故
> 任取 , 显然有
> 考虑 , 可得
> 于是可得
> 这里 表示 在 中的中心化子, 可以证明它等于 . 因此对任意 存在 使得
> 容易验证 是 的一个自同态, 因此任取 都有
> 由定理2.1不难验证 正是满足条件的 的自同态, 定理证毕.

由上面的定理, 我们实际上将求 的自同构转化为了求 的自同构和 的自同态, 最后留下几个关于引理4.2和定理4.3的结果作为练习.

求 .

实际上只需要求实数域的自同构(必为恒等映射)和非零实数乘法群的自同态.

当 时 (例子4.1)就是一个内自同构, 因此在引理4.2中如果 可以忽略情况(2).

直接用矩阵计算就行

在定理4.3的证明中有几个结论未加证明:

• 在 上的限制就是 的自同构
• 存在 的自同构 使得 最后一步中定义的 是满足条件的 的自同态

请读者加以证明.

利用引理4.2实际上可以求出一批线性群的自同构, 比如 (即 中行列式大于0的那一部分元素)和 等等. 一般线性群和特殊线性群就写到这里吧, 接下来打算写一下有关上三角矩阵构成的线性群的性质.

[1]: 华罗庚, 万哲先.典型群[M].上海科学技术出版社:上海,1963:69-76,193-210, 225-244.

title: 线性群的初等讨论 5 上三角矩阵群 - 知乎
permalink: https://zhuanlan.zhihu.com/p/128545791
author: ZCC
author_id: 6905106fcab33fc4f75aadffdd0fb07c
column: ZCC的代数随笔
column_id: c_1147084764438691840
voteup: 27 赞同
created: 2020-04-30T11:29:43
updated: 2020-04-30T11:29:43
fetched: 2024-06-09T18:23:43
count: 约 2997 字
version:
tags: [矩阵, 群论, 抽象代数, ZCC, ZCC的代数随笔]
url: https://zhuanlan.zhihu.com/p/128545791

from 专栏 ZCC的代数随笔

域 上所有n阶可逆上三角矩阵的全体构成 的子群, 记作 , 其中所有主对角线上元素都为1的矩阵构成子群 (也成为单位上三角矩阵群). 我们断言:

. 其中 表示所有n阶可逆对角矩阵的集合.

本节的核心结果是

是幂零类为 的幂零群.

幂零类(nilpotent class)是幂零群降中心列的长度减1. 例如幂零类为1的群是交换群, 幂零类为2的群是亚交换群.

定理5.2的证明方法有多种, 我们采取矩阵计算的方式简要说明. 详细的证明可以参看[1].

为了方便, 用 表示 阶方阵中当 时第 行第 列元素都为 的所有矩阵的集合, 即

令

显然 , 这样构造了一个序列

事实上上面这个序列正是 的一个正规序列, 并且有

(这里可以用繁琐的矩阵计算说明)

因此是 的一个降中心序列(事实上可以证明它同时也是升中心序列).

即有 是一个幂零群, 其幂零类为 .

是可解群.

这是因为 是幂零群 过幂零群 的扩张. 但要注意它未必是幂零的, 事实上, 就不是幂零的[2].

不借助矩阵计算的证明参考[3].

反过来有下面这个有意思的结果:

任何一个有限幂零群都同构于某个 的某个子群[4].

同样我们可以考虑 和 的自同构.

我们前面提到过 和 的自同构[5], 而上三角矩阵群的结果与之相似:

设 , 则存在 到 的同态 , 的自同构 , 中的某个元素 , 使得