RAID 6的数学原理详解 Binsky

By binsky in 开发笔记 2017年11月29日 3,035 views

• 为什么需要RAID

为了存储数据的可恢复性。

在存储数据同时，根据一定的数学原理存储适当的冗余数据。当存储介质（硬盘）发生一定范围的故障时，即使丢失了部分数据，在介质故障修复后，可以根据遗留的数据和冗余数据，恢复丢失的数据。

其原理类似于数字通讯领域所用的纠错码，不同的数据冗余模式就形成了不同的RAID类别。

在这里，需要冗余校验的数学模型，首先从单一冗余模型开始。

• 单一冗余模型

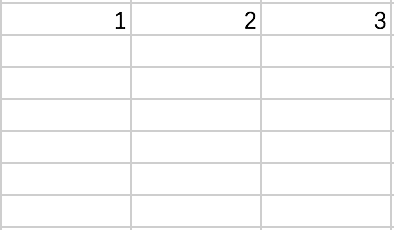
假设，要记录三组数据，如

6、18

26、32

87、98

可使用如下表格来记录

第一列第二列填入要存的数据，在第三列中填入前两列的和，如下如所示：

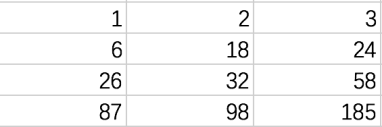
我们把第三列叫做校验和。

根据以上规则记录数据，可以得出结论，这三列中无论哪一列的数据丢失，都可以根据还健在的另外两列数据，还原丢失的数据。进而推论，即使是超过三列的情况，当任意一列数据丢失是，都可以根还健在的数据，实现数据的恢复。这就是单一冗余模型。

但是，以上求和的单一冗余模型，不会实际的数据存储中得到应用。可以看到，校验和的总容量，要等于所有数据的总和。也就是说，这个单一冗余模型，其效果是和把所有数据抄一份，分开保存一样的。

这种原样复制的单一冗余，就是RAID1。

为了节省冗余冗余空间，有人想到用异或算法（XOR）来替代简单的加法。现代计算机的异或运算性能非常好，无需更多的专门运算器。同时异或算法完全满足正运算与逆运算的完全映射(即，正运算的结果唯一，同时这个正运算的逆运算结果也唯一，满足交换律和结合律。而且，异或不会升位。

用异或算法（XOR）改写后的存储记录如下：

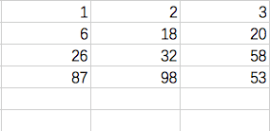
第三行的校验和，不论多少个数据成员，用异或得到的校验和容量不会累加。

为了更好的概括，我们用“+”表示这个正向的校验运算，用“-”表示其逆运算。假设有n个存储成员，其中成员1到n-1成员为数据，成员n为校验和，则异或算法（XOR）的校验关系如下：

D1 + D2 + D3 + … +Dn-1 = P1

Dx = P1 – D1 – D2 – D3 – … -Dn-1(Dx为丢失的存储成员)

也就是：

Dx = P1 + D1 + D2 + D3 +… +Dn-1(Dx为丢失的存储成员)

在这一模型中，校验和所需的存储不会太大，并且无论丢失哪一个存储成员，都可以根据还健在的数据恢复。

RAID 5就是基于这样的数学原理实现的。RAID 5至少需要三块硬盘，当RAID5的一个磁盘数据发生损坏后，可以利用剩下的数据和相应的校验信息去恢复被损坏的数据。

• 多次冗余模型

单一冗余存储只支持一个存储成员丢失，在实际运用中，有可能需要更高的冗余性，实现在缺失2个成员的情况下，存储整体依然可以恢复。因此要对单一冗余模型进行扩展，有人想到了二元一次方程组：

aX+bY=c

dX+eY=f

其中a/d != b/e

以上简单的二元一次方程组用到了乘法与除法，满足乘法交换律、结合律、分配律，并且乘除法计算完全可逆。

但如同单一冗余模型的简单加法一样，简单的乘法同样会导致校验容量大规模增加，因此不可取。在实际应用中，使用的是基于伽罗华域（Galois Field，GF，有限域）的乘除法。

以GF(2^8)为例，我们设计一个有限循环域，域上仅有0-255这几个数字，这些数字之间再设计一个完整的加减乘除运算，其结果依然在这些数字中，而且运算结果唯一，无二义性。

我们来设计一种算法，对于2，如果2的n次方大于某个值(本原多项式),则让其对这个值(本原多项式)取余，确保又折回到0-255这个范围内，如果从2^0,2^1,2^2,,,直到2^255，按这个规律做运算，得到的值均处于0-255范围内，且均不相等，这样就形成了一个一对一的映射关系，同时满足2的这些次幂与结果之间就乘法/除法的运算规律(具体理论需参考群、环、域、有限域等数学理论)。

在GF(2^8)上，有16个满足条件的本原多项式，分别如下：

1 x8+x7+x6+x5+x4+x2+1 1 1111 0101 = 0x1F5

2 x8+x7+x6+x5+x2+x+1 1 1110 0111   = 0x1E7

3 x8+x7+x6+x3+x2+x+1 1 1100 1111   = 0x1CF

4 x8+x7+x6+x+1 1 1100 0011                = 0x1C3

5 x8+x7+x5+x3+1 1 1010 1001              = 0x1A9

6 x8+x7+x3+x2+1 1 1000 1101              = 0x18D

7 x8+x7+x2+x+1 1 1000 0111                = 0x187

8 x8+x6+x5+x4+1 1 0111 0001              = 0x171

9 x8+x6+x5+x3+1 1 0110 1001              = 0x169

10 x8+x6+x5+x2+1 1 0110 0101            = 0x165

11 x8+x6+x5+x+1 1 0110 0011              = 0x163

12 x8+x6+x4+x3+x2+x+1 1 0101 1111 = 0x15F

13 x8+x6+x3+x2+1 1 0100 1101            = 0x14D

14 x8+x5+x3+x2+1 1 0010 1101            = 0x12D

15 x8+x5+x3+x+1 1 0010 1011              = 0x12B

16 x8+x4+x3+x2+1 1 0001 1101            = 0x11D

常用0x11D做为raid6的本原多项式，意思是2的n次方如果大于0x11D，就对于做xor的取余运算，确保结果小于0x256，这样就可以算出2^0到2^255之间的所有数值。

GF(2^8)上的加减法同样是异或算法(xor)。

GF(2^8)上的乘法即多项式乘法，但依然要对本原多项式取xor余，在算法设计上，有多种计算方式，但在GF(2^8)上，最快的推荐方法是查表法，只需事先计算好所有的0~255 分别乘以 0~255的值，生成65536个值的表格，计算时直接查表即可。也有使用对数查表法，使乘法转变为加法进行运算的，需要查表和加法结合使用。

GF(2^8)上的除法可转换为对其逆元的乘法，即a 除以 d，假设d对应于(x的m次幂)，那找出对应(x的255-m次幂)的值d’,a除以d，即等于a乘以d’。

• RAID6

基于伽罗华域（Galois Field，GF，有限域）的乘除法都确定后，二元一次方程组：

aX+bY=c

dX+eY=f

其中a/d != b/e

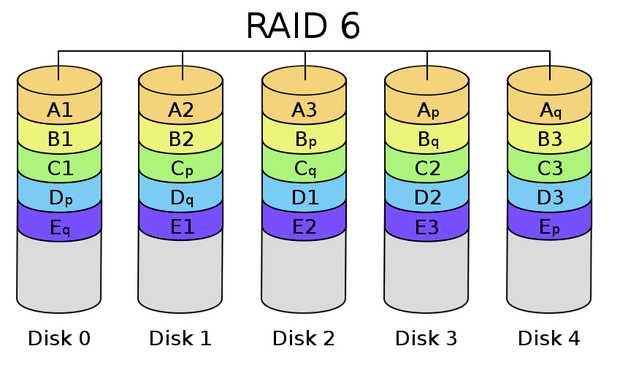
就可以求解了。所以，一个以此原理生成的RAID的结构设计大致如下图(以5块盘为例，P为第一重校验，Q为第二重校验，xn为数据)：

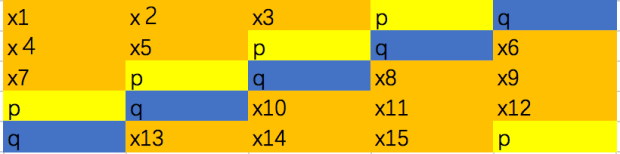
之所以P和Q螺旋式循环分布，是为了使所有磁盘负载均衡，如果不好理解，可以把P和Q单独放在一列中，算法的意义是相同的。

再重复一下，下面提及的+、-、*、/运算都是指基于GF(2^8)上的加、减、乘、除

P值等于同一行(条带)上的所有单元相加的和。或者可以理解为1与每个单元相乘后的累加和，如第一个条带的P：

P= x1+x2+x3 也就是P=1_x1 + 1_x2 + 1*x3

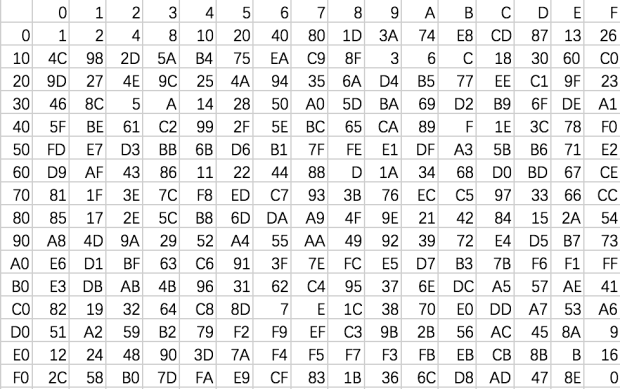
在GF(2^8)上，每个多项式对应一个0~255的值，即d0对应多项式X的0次幂，d1对应多项式X的2次幂等，按多项式展开，X为2进制，故d0 = 1，d1 =2，d2=4 ，d3=8，等等，如下表所示：

返回RAID结构图中，Q值等于每个数值单元格乘以他们的相应的dn再累加的结果，其中dn可约定，只需保证同一条带的运算中不重复出现dn即可，如第一行的Q可以为：

Q = d1* x1 + d2_x2 + d3_x3

这样，对于每一行(条带)，就可以保证任意2个单元丢失，都可以计算出来。

以第一行为例:

a) 如果P、Q均丢失，数据区不影响，x1、x2、x3均可正常读写

b)如果xn丢失，根据P或Q都可计算出来(实际中，因P 的计算更快速，通常会使用P校验计算出丢失的 xn)

c)如果P、xn丢失，P值不做处理，假设丢失的是x2，根据Q值的定义

Q = d1* x1 + d2_x2 +d3_x3

=> d2_x2 = Q + d1_x1 + d3*x3

=> x2 = (Q + d1_x1 + d3_x3) * x253 ;//注：x253为x2的逆元，可以查表得到

d) 如果两个x丢失，则可根据二元一次方式的标准解法进行求解，假设丢失的是x1,x3：

P = x1+x2+x3

Q = d1* x1 + d2_x2 +d3_x3

=> x1 = P + x2 + x3

=> Q = d1 * (P + x2 + x3) +d2_x2 +d3_x3

=> Q = d1_P + d1_x2 + d1* x3 + d2_x2 + d3_x3

=> Q = d1_P + d1_x2 + d2_x2 + d1_x3 + d3*x3

=> Q + d1_P + d1_x2 + d2*x2 = (d1+d3) * x3

=> x3 = ( Q + d1_P + d1_x2 + d2*x2) / (d1+d3)

查表法得到(d1 + d3)的逆元dn后，可知

x3 = ( Q + d1_P + d1_x2 + d2*x2) * dn

再根据P= x1 + x2 + x3求得x1，即完成所有数据的补缺。

RAID 6必须具备四个以上的磁盘才能生效，可使用的容量为硬盘总数减去2的差，乘以最小容量。

[一沙一世界，一花一天堂](https://www.binsky.net/index.php/11.html "一沙一世界，一花一天堂

        一沙一世界         一花一天堂         双手握无限         …")2014年12月4日在“读书笔记”中

[SVN和Git的区别](https://www.binsky.net/index.php/898.html "SVN和Git的区别

  Git是分布式的，SVN不是 这是Git和SVN的根本区别。Git和SVN一样，都有中…")2016年11月26日在“Git”中

[坂上之云——明治时代的荣光](https://www.binsky.net/index.php/36.html "坂上之云——明治时代的荣光

        如此渺小的国家，迎来了他的开化期，说到小，恐…")2014年12月23日在“影视”中

Tags raidw冗余数据

原网址: 访问

创建于: 2020-08-17 12:33:41

目录: 无

标签: www.binsky.net