如何直观地理解群论? - 马同学 的回答
title: 如何直观地理解群论? - 马同学 的回答
url: https://www.zhihu.com/question/23091609/answer/127659716
author: 马同学 (a43edcdd0ac3d2e1473023ed0af0bf2a)
voteup: 3069 赞同
created: 2016-10-21 05:46:40
updated: 2016-10-21 05:46:40
fetched: 2021-10-12 08:53:20
count: 约 5513 字
version:
tags: [数学, 抽象代数, 离散数学, 群论, 多项式方程]
问题描述
大部分同学在学习代数学时,都会被一大堆的概念搞得晕头转向。
几年前,我刚开始看线性代数时也是这样,完全不明白为什么要定义这些奇怪的东西。直到后来看到《如何直观理解矩阵和线性代数?》、《理解矩阵(一)》等文章,才豁然开朗。我非常认同《理解矩阵(一)》文中强调数学直观性的观点。
那么,应该如何直观地理解群论?群论中一些主要的概念究竟是为什么、怎么样引入的?
【参考问答】
话题:
数学, 抽象代数, 离散数学, 群论, 多项式方程
回答:
群论不简单么?一个集合和一个二元运算,并且满足群论四大公理。黑纸白字,没有一个符号、一个汉字是我不认识的。经过这么多年的数学训练,加上刷题,那是想证明就证明、想计算就计算,砍瓜切菜、手起刀落、猛虎下山、势如破竹。
但是!我很不爽,这种感觉好比有人叫你去砍人,你也不问问为什么,一言不合就出手把人砍翻在地,或者被人砍翻在地,这种行为我们一般把它成为脑残,你的身份就是别人的小弟。
我们不要做数学的小弟,刷题不能给我们自由,唯有思考可以。
下面就讲一下我对群论的一些思考。
1 集合
讲群论先从集合讲起,集合简单来说就是把一堆东西放在一起(暂时就别提罗素悖论了):

可是这用处不大啊,东西之间得有相互作用才能更好的描述世界啊:
东西我们把它称之为对象,对象之间的互相作用我们称之为操作或者运算。
自然数 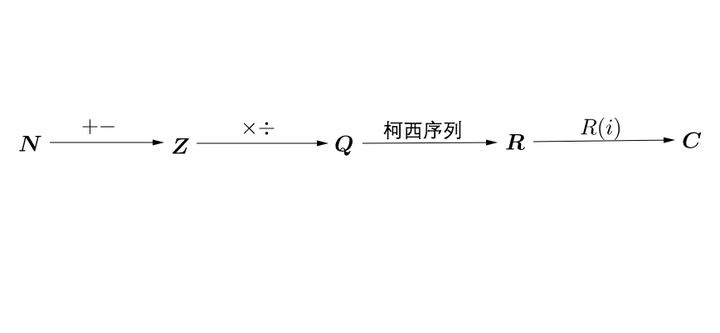
运算不止加减乘除,数学学到后面就多了很多抽象运算。甚至从集合和运算的角度来看,学数学的过程很多时候就是在不断的扩大对集合和运算的认知。理解的集合和运算越多,相关领域的数学基本上也就理解了。
其中有种特殊的 集合+运算 就是群。
2 群
简单来说,群的作用是描述对称。
2.1 什么叫对称?
我们来看看:
- 正方形对称吗?
- 物理定律对称吗?
- 多项式的根对称吗?
上面的问题的答案都是:对称!
对称就是: “某种操作下的不变性” ,关键字是两个: “操作”和“不变性” ,要说明这点让我们通过上面的三个问题来理解。
2.1.1 正方形是否对称?
先看看正方形,其实它对称是蛮明显的,符合我们日常的语义,可是我们也要把它放到数学的语境里来分析一下: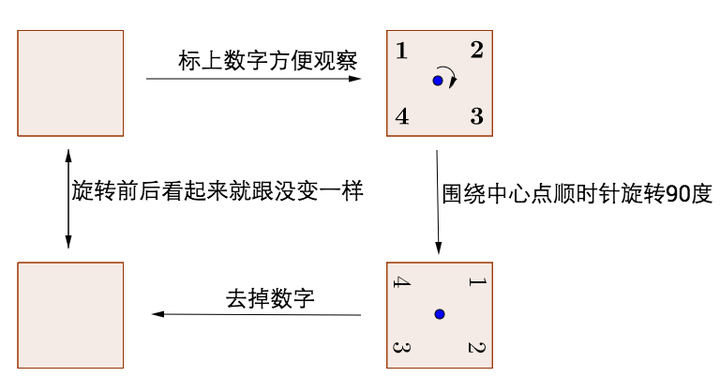
围绕中心点旋转这个 操作 ,正方形所具有的 不变性 就是对称。
我们换一种操作,正方形也可以对称: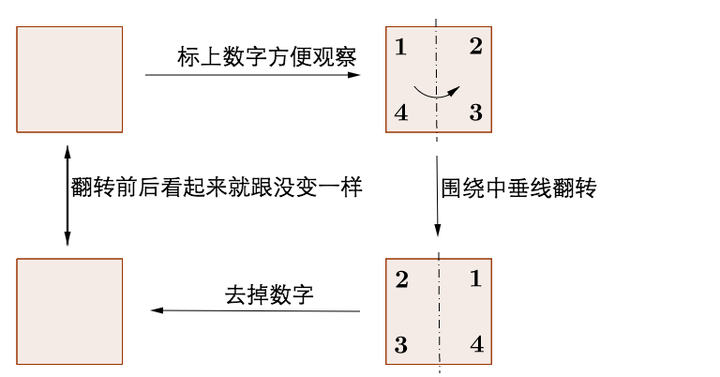
围绕中垂线这个 操作 ,正方形也具有 不变性 ,也是一种对称。但是因为操作变了,所以这种对称和上面的那种对称不是同一种对称,之后我会再说到这个问题。
假如刚才的正方形只是桌子的桌面,继续围绕中垂线翻转这个操作就不对称了: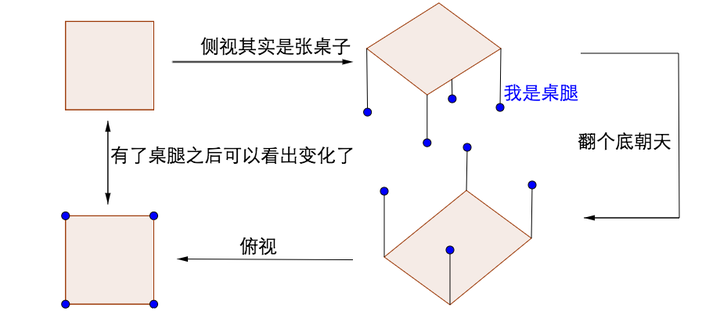
2.1.2 物理定律是否对称?
这个听起来就有点奇怪了,但是从不变性的角度出发,相对于时间流逝这个操作,物理定律保持不变,我们可以说物理定律相对时间对称。相对于空间改变这个操作,物理定律保持不变,我们可以说物理定律相对空间对称:
这听起来蛮哲学的,不是说数学学到后面都是哲学吗?
物理我属于民科水平,大家可以参看 对称性----维基百科 。
2.1.3 多项式的根是否对称?
说明下,多项式方程指的是形如
群论就是从解多项式的根开始发展起来的,所以自然要谈一下为什么多项式的根具有对称性。
首先要从简单的一元二次方程说起:
从上图中来看,相对于
这个对称性有什么用?根据 韦达定理 ,一元二次方程
所以顺便说一下,群论的发展过程是这样的: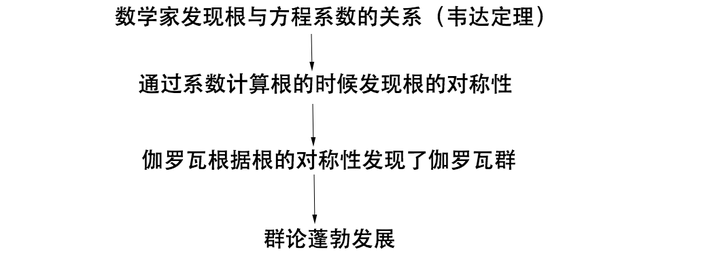
关于伽罗瓦与一元五次方程的问题,与群紧密相关,但是又涉及到更多别的知识,本文就不继续推下去了。
2.2 对称如何用数学表示?
让我们从正方形开始解读如何来表示对称.
之前说过,对称最重要的是在 “某种操作下的不变性” ,所以我们先讨论正方形围绕中心点旋转,总共有4种对称操作:
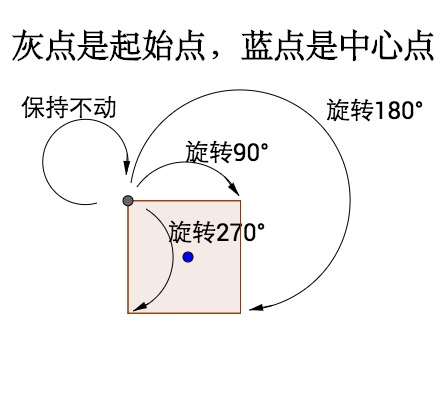
或许你觉得应该不止4种操作,比如转两圈,这可以等价于“保持不动”,而转45°,这会导致不对称(因为你会明显发现变化)。
起始点是完全不用关心的: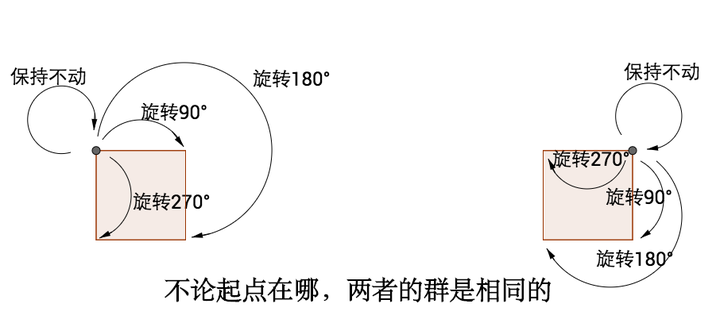
甚至是不是正方形也不重要: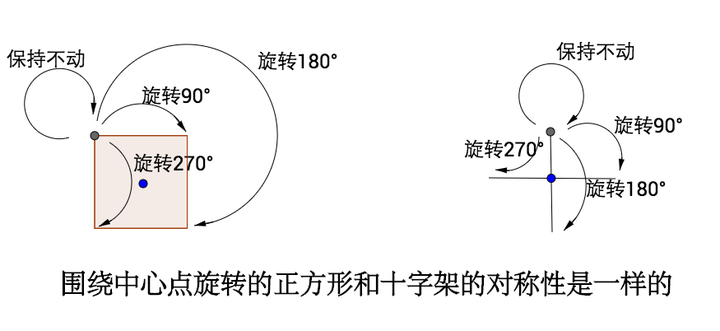
是的,群只关心对称最本质、最抽象的性质。所以我们只关心操作,只需要把操作放到集合里。
要放进去我们必须要把操作给数学化,也就是符号化,我们起码有两种符号化的选择,类比于加法或者乘法:
稍微解释一下,什么叫做类比于加法?比如我们通过类比于加法得到
还要说明的一点是,这里的加法和乘法是模加法、模乘法,类似于钟表,按照12小时制算,
这样我们就得到了两个群,一个是
这里先用到群的解析式了,下面就要解释一下。
2.3 群的定义
先祭出大杀器,群的标准定义:
群是一个集合
,连同一个运算" ",它结合任何两个元素 和 而形成另一个元素,记为 。符号" "是对具体给出的运算,比如整数加法的一般占位符。要具备成为群的资格,这个集合和运算 必须满足叫做群公理的四个要求:
- 封闭性:对于所有
中 ,运算 的结果也在 中。 - 结合性:对于所有
中的 和 ,等式 成立。 - 单位元:存在
中的一个元素 ,使得对于所有 中的元素 ,等式 成立。 - 逆元:对于每个
中的 ,存在 中的一个元素 使得 ,这里的 是单位元。 维基百科
数学是自然科学的语言,和日常的说话相比最大的优点是精确没有歧义,缺点就是晦涩不好理解。群的定义也是这样,下面我们用人话来解释群。
套用正方形的例子来解读群的定义,选
- 集合里的对象:所有保证对称性的操作。
- 二元运算:模加法。
- 封闭性:操作相加还是在集合内,比如
- 结合性:
- 单位元:保持不动就是单位元,映射为0,所以
- 逆元:首先旋转正方形的操作是可逆的,所以
其实吧,我可以再抽象一点,
2.4 群的结构与同构
之前说过,正方形围绕中垂线翻转是不一样的对称 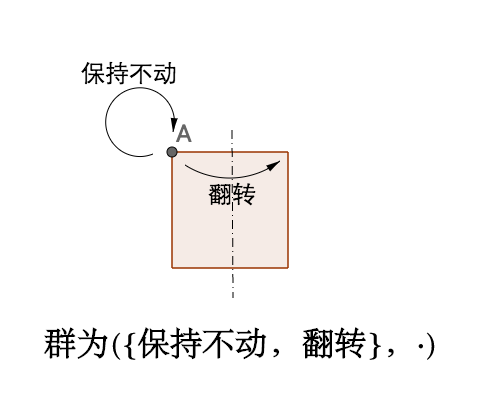
上图我把运算直接表示为"
现实中,还有各种各样的对称,比如正方形和圆:
这两种对称的结构也不同,对应的群也不一样。群论就是对各种群的研究。
2.5 进一步的思考
关于同构,这里再进一步思考,圆是有无数种对称操作的,之前提到的相对于时间对称的物理定律,也是有无数种对称操作的(因为时间是可以无限流逝的),从某种意义上讲,两者是不是同一种对称,也就是同构?如果是同构,那么我只要研究一个群就可以研究两者了。
思考,才是数学最大的乐趣所在。
最后推荐一本书,Visual Group Theory Nathan Carter,谢谢 @金凯。这书我以前看过,挺好的,就是没有中文版,贵。
评论:
真澄: 怒赞! 只有通彻理解了理论本身,才能用最直观最清晰的语言去体现其内涵。不像有一些人开始试探性的抛出一个专业名词,当察觉到你满眼狐疑一脸不解的表情时,紧接着就是更多的专业名词堆砌,我觉的这种行为除了满满的装逼之外没有半点实际的意义。 (115 赞)
马同学 -> 真澄: 只能说,数学教育和数学研究确实是有天壤之别。谢谢手动点赞。 (84 赞)
知乎用户: 我们不要做数学的小弟,刷题不能给我们自由,唯有思考可以!!!~~~ (62 赞)
夏天爱吃西瓜 -> 知乎用户: 挖到重点! (3 赞)
Legallchaper1 -> 知乎用户: 可是不刷题光看课本搞不懂啊[大哭](中学范围内) (1 赞)
知乎用户: 看过的教材全都是上来就亮大杀器,还给扩展出五六个运算性质的,接着就上李群和阿贝尔群,我全程蒙蔽,都不知道群到底特喵有个喵喵用,现在算是有那么点感觉了 (25 赞)
马同学 -> 叶聪: 学习,最好的是先建立一个合理的模型,然后后面的就好办了。 (5 赞)
「已注销」 -> 叶聪: 数学系的毕业了看一看还是看不懂 我挂了两年的抽代 (8 赞)
「已注销」 -> 马同学: 数学系的毕业了看一看还是看不懂 我挂了两年的抽代
马同学 -> 「已注销」: 这是抽代最基本的了,所以你确实挂的不冤:) (1 赞)
柚子鹭:
大学学文科的进来一看,咦我好像能看懂
但瞬间觉得自己民数了😂数学哪有这么好懂啊 (17 赞)
JSC -> 柚子鹭: 同文科,也能看懂,但是做题,算了。 (4 赞)
Peng-hui Guo: 弱弱的问一下:群论到底对应什么实际问题?? (4 赞)
马同学 -> Peng-hui Guo: 比如,群论预言了物理学里面的基本粒子模型,八重态和十重态,之后才被实验所证明,指明了发展方向。 (27 赞)
打火机不好吃 -> Peng-hui Guo:
这是一个很有趣的问题……函数有什么用?你觉得呢?作为一种研究工具,它可以有无限种用法,只要你能想到。初等物理(高中)都是用函数和方程来研究的。群论不过是更高级的一种工具而已。比方说可以用群论来研究魔方问题=
= (13 赞)
笑旺旺 -> Peng-hui Guo: 群论揭示了数之间的对称规律,描述了一种显而易见但以往数学都没能好好描述的规律。只要是规律,就有预见性,一些物理现象数字化后代入套进来,就可以预测新的物理现象,成了物理规律。 (7 赞)
那卡 -> 笑旺旺: 群论不揭示规律 是让规律更明显的一种工具。 到底来说 规律还是算另外的发现 (3 赞)
做吉他的汉斯 -> Peng-hui Guo: 是一种思维工具,帮助人们发现新的现象。 (3 赞)
Leo -> Peng-hui Guo: 额那个正方形标数字让我想到同分异构体 有机化学这个让我烧火丫头拿钥匙做不了主的东西
Leo -> Leo: 位置关系是相对的辩证的
Leo -> Leo: 我还要评论,那些排列组合,那个生物遗传的互为验证,全是这玩意在作祟
Frederic: 知乎多点这样的文章就更好啦! (13 赞)
自由像风儿一样: 我没学过,但是好像发现了一点问题不知对不对,想请教一下。就是讲道逆元那里你说 r+(-r)=0可以称(-r)是r的逆元,-r不是这个群内的元素, (12 赞)
马同学 -> 自由像风儿一样: 是的,你说的对,你看得很仔细。其实-r也就是3r,只是我跳过了这一步就直接给出了-r (8 赞)
董豆饼: 小时候就知道伽罗华和群论的故事,现在终于得科普了一回😂<( ˘ ³˘)/🌹 (7 赞)
马同学 -> 董豆饼: 本文离伽罗瓦群还有老长的一段距离:( (7 赞)
董豆饼 -> 马同学: T_T伽罗瓦大神
JSC -> 马同学: 群论一般怎么出题?
小雨 -> 马同学: 不远了,只要证明中间域到伽罗瓦群的子群之间有一一映射就快完了[笑哭] (1 赞)
三十年前: 我恨数学家! (6 赞)
李翔宇 -> 三十年前: 死了都不让别人好好活 (14 赞)
小怂蛋的好爸爸 -> 三十年前: 我不恨 (2 赞)
JSC -> 三十年前: 经历了什么?
Leo -> 三十年前: um yes 看看拉格朗日 笛卡尔干得好事情
望天冲:
我要说,从对称性入手,介绍群论,实在是太绕了,这种人,自己都没真正整明白群论。只不过是,人云亦云,鹦鹉学舌而已。
见我的书《低级群论》,多谢指教! (3 赞)
望天冲 -> 望天冲: 群之所以显示某种对称性,是因为其元素分层次的平等,分层次的概率相同。注意这个分层次。
马同学 -> 望天冲: 感谢指教,苟日新,日日新,又日新。
胡柴 -> 望天冲: 不要叫低级群论。改成群论基础入门,基础群论,群论入门,群论导论,群论小议等都行啊。 (2 赞)