最小作用量原理、莫培督原理、哈密顿原理、变分原理分别是什么? - 因物悦理 的回答
问题描述
如题,这四个概念什么区别,或者哪个概念包含哪个概念?这些概念或者原理又有哪些异同点与联系 麻烦讲详细点
变分和全变分什么区别?对时间和对路径积分又分别是什么?还有作用量究竟是什么(不是问哲学上的什么,我是问数学形式上是什么)?
话题:
理论物理, 理论力学, 泛函分析, 变分法, 分析力学, 因物悦理
回答:
这个跨度融在一篇里, 是好主意吗? 得想想
自己感觉这篇幅有点长了, 读者可能前半部分还能坚持, 但全读完真是累
或者说, 违背了在一篇文章内大致获知信息量的预期
作者应该是高中老师
前言
最小作用量原理被称为物理中的“第一性原理”,其地位可见一斑。我出于对物理规律普适性的向往,折腾了三个多月写出这篇三万七千字的长文,终于了却了自己的这个心愿。
本着自己懂不如大家懂的原则,我尽力把文字写得很通俗。作为文章里最大的拦路虎——数学,以高中生所具备的基础出发,我遵循懂思想、重定义、足够用的原则娓娓道来,其难度绝对赶不上高考数学题。信不信由你,你敢挑战不?

一、伟大的牛顿运动定律之困惑

神人牛顿出版的著作《自然哲学的数学原理》里,众人皆知的牛顿运动定律和万有引力定律给人类认识自然提供了有力的武器,以至于牛顿之后的科学家认为只要找出物体的受力和运动的初始条件,就能搞清楚物体之后的运动规律。从这个角度来说,牛顿的光环太耀眼,导致18世纪的物理学界再没出现过像他这样的集大成者。虽然如此,但是在具体的复杂问题中怎样把牛顿运动定律变得好用还是大有可为的。
牛顿运动定律是为回答物体怎样做机械运动而生的一个力学体系, 也就是要弄清楚物体的位置随时间会发生怎样的变化 。要完成这一光荣的使命,牛顿运动定律其实是会挑对象的—— 研究的物体要能被看成质点 。
什么?要知道质点本就是个理想模型,现实世界里哪有真正的质点呢?要是牛顿运动定律只能用在质点身上,那它岂不是一点用都没有?
别急别急,我不是这个意思。对于实际的物体来说,虽然不能把它看成质点,但是可以把它看成由大量质点组成的集合呀。对于这个集合体来说,若这些质点的运动都一样,咱们依旧能用一个质点来做个代表;否则就必须隔离每个质点进行单独地详尽研究。高中物理里的“板、块”模型就是这样一类典型问题,有没有想起被它支配的恐惧呢?要是再多几个板或块,是不是就想直接放弃了呢?
“板、块”已经是非常简化的模型了,要是换成杆呀、滑轮呀、支架呀等更实际的部件时,岂不是更要头大?究其原因,就是往往需要咱们隔离各个对象进行分析。然而更要命的是这些实际的部件会给咱们的待研究对象施加各种各样的约束,而且这些约束对于对象施加的作用力几乎都是事先未知的。
等等,约束是个啥?简单的说, 就是物体不能随心所欲地运动,其运动轨迹被这些器件限制在某条线或者面上 。
呃,干嘛要去研究这些复杂的器件呀,这不自讨苦吃嘛?嗨,谁说不是呢,可是历史的车轮来到了工业革命,哪个机器上不带点这些器件呢?而各种机器的制造不得依靠理论指导实践么?这不,大家的目光自然就落在了牛顿运动定律身上了撒。牛顿运动定律虽然是强有力的理论武器,但是当用它解决这些形形色色的约束问题时也会显得困难重重。
另外,牛顿运动定律用在复杂问题中显得麻烦的原因还在于其核心——
要是再考虑约束条件带来的方程,总的方程数量会更多。这还只是针对一个对象的方程数量,要是涉及更多的对象,其方程总数就多得去了。
这里只看一个高中物理里的简单例子就能有所体会。一个质量为

为了写出分量方程,这里将圆心选为原点,建立如上图所示的直角坐标系。则写出的方程为:
方程组里除了质量
这里的
看完上一段文字是不是一脸蒙圈?圆周运动哪有这么干的呢?不应该是在
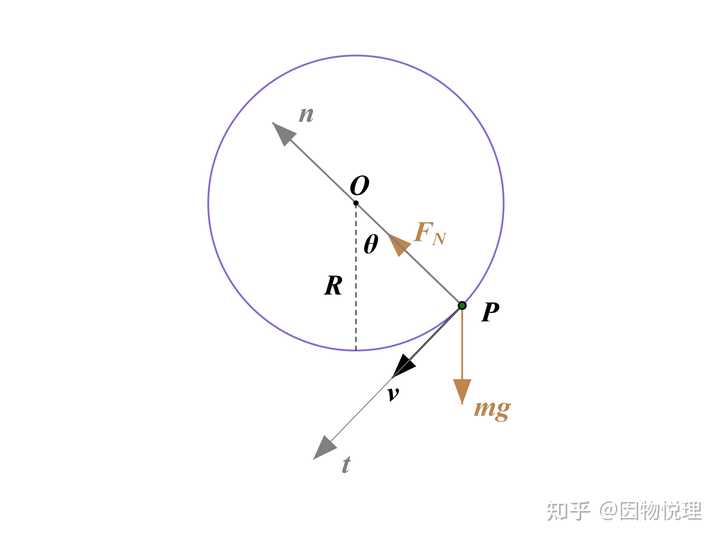
对对对,你说得都对,这么干确实简单得不得了。因为法向方向的方程为:
这么一来,轨道对小球的支持力就直接给求出来了。 请注意一下这里的因果关系:支持力的大小是随着速度大小的变化而变化的,其值事先未知 。
假如我不关心支持力,只想知道小球沿圆周运动时的速度大小的变化特点,那么切向方向的方程送给你:
至于切向加速度与速度之间的关系可以通过简单的微分方程来确定。
天呐,不仅方程数量锐减,而且求解难度也大大降低了!你对物理又开始爱了吧?
细心的读者可能已经发现了,咱们不过是换了一个坐标系而已,依旧是用牛顿运动定律的套路来求解问题。本来嘛,这不正显出了牛顿运动定律的伟大么?管天管地管空气,牛爷就是这么傲娇。但是咱们要思考的是:更换坐标系是不是一种简化计算的通用方法呢?面对数量众多的矢量分量方程,咱们能有更好的办法来精简方程数量吗?
这些问题亟待大神们各显神通去解决,咱们在瞻仰大佬们的成果之前得先增添一些简单的数学武器。毕竟工欲善其事,必先利其器。
二、并不可怕的微积分
有关微积分的思想,大家可以去阅读我之前写的文章(戳我)。这里将围绕着微积分的定义引出后面要用到的一些工具。
说到微分就必须先提到导数。无论是某些物理量的定义——比如速度
以形象直观的图形来说,要反映图中倾斜直线的倾斜程度,显然是图中的角度
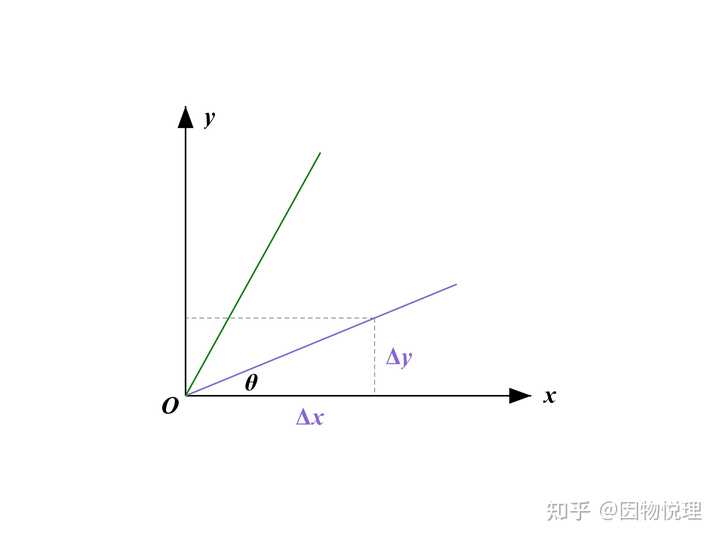
从图中可以发现,对于直线来说,无论哪一段的倾斜程度都是一样的。这很好理解,如果物体始终做匀速直线运动,无论用哪一段的位移除以对应的时间,求出来的速度都是一样的。但是相比直线,曲线更常见;对于运动来说,变速运动也更常见。如此一来,曲线上不同部位的倾斜程度就不一样了。 所以我们就会更关心曲线上每处的倾斜情况如何 。
那么问题就来了,过曲线上一点可以画出无数条直线,哪条直线才是反映该处的倾斜程度呢?
从直线斜率的计算可以看到,要出现
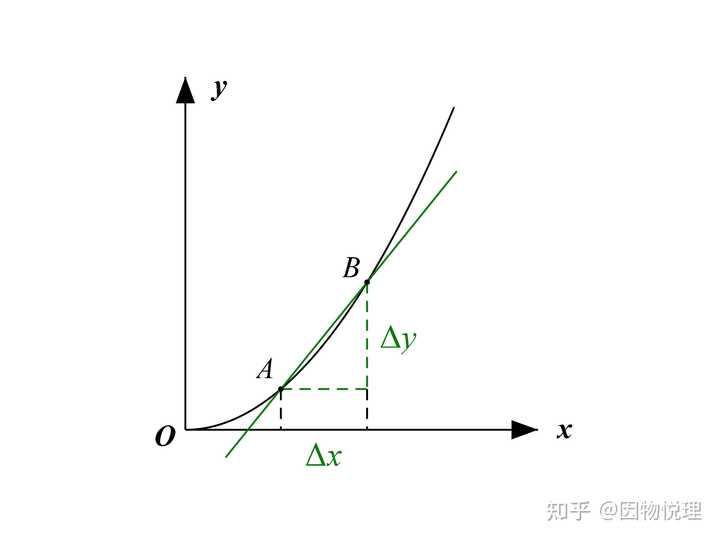 割线AB
割线AB
但割线的斜率并不是我们需要的,因为取不同的
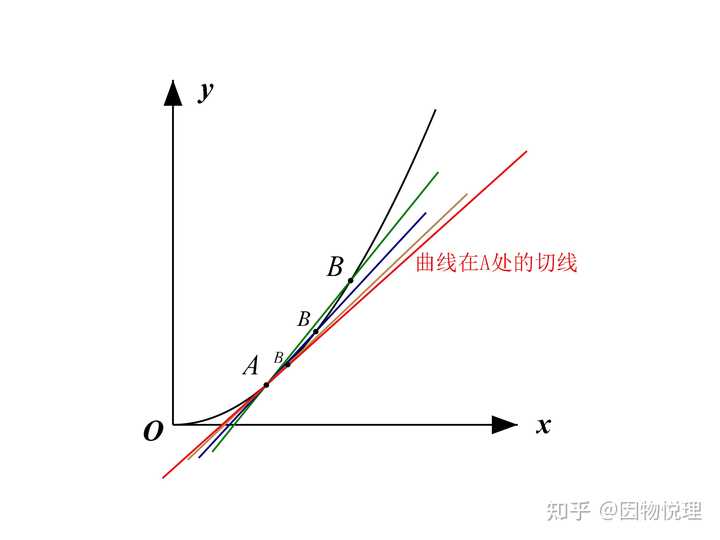 割线变切线
割线变切线
这么一来,我们就发现割线变成了曲线在
由于曲线都有对应的函数来表示的,而数学里又习惯把函数写成
于是切线的斜率被写成如下的形式,并获得了一个新名字——函数的导数,记为:
别怕哈,这一坨表达式看起来好吓人,其实很简单——因为函数的导数就是该函数曲线在某点处的切线斜率。所以,只要你知道啥是斜率,看懂这个表达式肯定不在话下。
不过咱要啰嗦几句,记作
请注意,不是
导数说完了就可以说微分了。还是看图中的切线,其与竖直虚线相交于
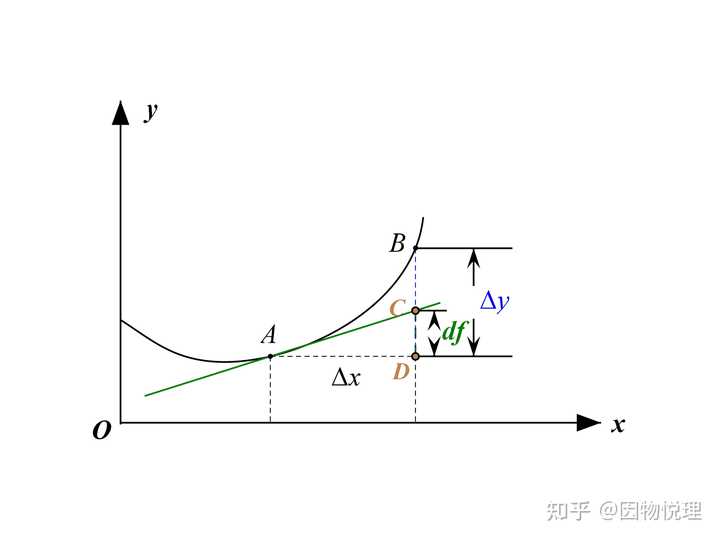
由于
咱们就是把
由于自变量
这么一来,函数
或者记为:
这和刚才导数的符号不同,这里是指函数
说完了这两个重要的概念后,就能根据定义得到几个重要的结论。这些结论在数学教材里都有严格的证明(都很简单明了),大伙自己去看书也挺香的。悦理君就当给大家留个练习哈。
常数
两个函数相加减的结果,其导数等于每个函数的导数相加减,即:
两个函数相乘的结果,其导数为:
这个结果记起来稍微要费点脑子: 你可以想象自己一个人带着两个娃,现在得给娃脱衣睡觉,你是不是得挨个来?先给第一个娃脱衣服,让第二个娃一边呆着(
至于两个函数相除的导数就不写了,后面的物理问题里暂时用不上。毕竟这篇文章的主角是物理,数学工具够用就行。
另外,还有一个重要的结论就是复合函数的导数。复合函数你可以想象成是套娃,函数
所以函数
详细严格的证明过程请自行阅读数学教材。
这个等式的识记也好理解,相当于你的娃现在穿了两件衣服,你是不是得一件一件的脱?而且是先脱外层的衣服
以上是关于求导的结论,而求导数的基本法则也就是求微分的基本法则,只是形式上稍微变一变就可以了。比如:
看到这里,是不是觉得微分理解起来也不难呀?本来嘛,当你理顺了概念的来龙去脉搞,由它衍生的结论也就手到擒来了。大家往后继续看就会发现,这种学习方式被悦理君体现得淋漓尽致。
回来继续唠嗑微分。前面我是用只含一个自变量的一元函数带领大伙叩开了微分的大门,但是更多的函数所含有的自变量不止一个,这样的函数被称为多元函数。它们的微分会不会有啥不同呢?
咱们就看看最简单的多元函数,即函数含有两个自变量
如果函数
偏导数 partial derivative 的定义是:一个多变量的函数(或称多元函数),对其中一个变量(导数)微分,而保持其他变量恒定
偏导数符号 ∂
其结果为:
同理,如果函数
其结果为:
有了多元函数的偏导数概念,类似于一元函数的微分,则多元函数的微分就是:
说完了微分说就该说一说积分了,从如今的“微积分”这个名称上就能看出它俩可是一对形影不离的好基友。不过要想发现它俩的基情,着实要下一番功夫。
积分起源于对封闭图形的面积计算。你肯定能很快写出矩形、三角形或者梯形的面积计算公式,但是面对一般的封闭图形时就无能为力了。不过没关系,咱可以用那些规则图形的面积来逼近这个不规则图形的面积。这就好比铺地砖一样,总能用规则的地砖近似地铺满一块区域,至于边边角角可以用更小的规则地砖将其覆盖,直到最后看不出什么缝隙。
那这种朴素的思想如何用数学语言来描述呢?假设有一条函数曲线
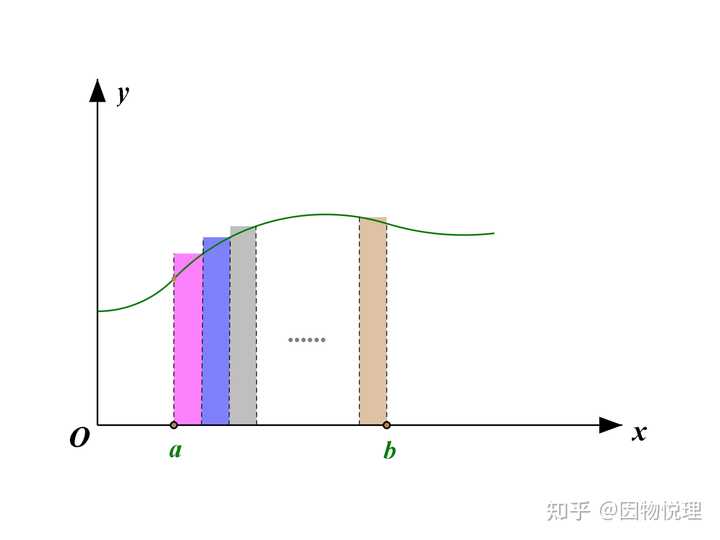
至于所有矩形条的面积和能不能代替曲边梯形的面积、以及代替的误差有多大,这有严谨的数学论证,咱就省略几千字了哈,数学教材可是等着你们去宠幸呢。显然此处只关注能精确替代的情形, 即把区间
这个式子称为被积函数
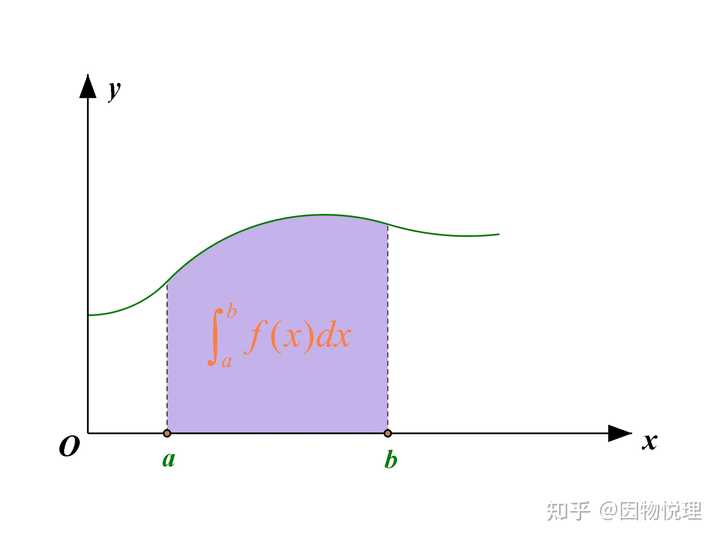
显然定积分
这是肯定的撒,比如说函数是二次函数,无论写成
为啥要啰嗦上面这么一段文字呢?还不是担心你对接下来的表述弄混淆了嘛。既然定积分
看到这里,你是不是就想起了函数?变动的积分上限有与之一一对应的数!把这个函数起名为积分上限函数,记作
其中
你看, 我可是特意把积分变量换成了
弄这么多铺垫给你甩出积分上限函数可不是为了让你练习拗口令,而是这个函数有个及其重要的性质——积分上限函数的导数等于被积函数,即:
等式成立的条件以及证明过程就请各位辛苦一下翻阅数学教材了,很简单、很容易看懂!
这个性质一下子就把求导和定积分给联系起来了。求导或者求微分是对函数的一种运算,那么这种运算就有与之对应的逆运算,就好比加法的逆运算是减法,乘法的逆运算是除法。如果函数
则函数
对了,你还记得常数
所以新函数
鉴于求原函数是求导的逆运算,而且原函数就长成
也就是说不定积分是一种运算,是微分运算的逆运算。请不要把它和定积分搞混了哈,人家定积分是一个数。
什么?你要问定积分怎么算?积分上限函数笑而不语地向你招了招手。假设
发现没,只要令积分上限里的
不过还有一个小问题就是任意常数
于是可得:
再令积分上限里的
即定积分
完美收工!这便是大名鼎鼎的牛顿——莱布尼茨公式!是它把定积分的计算与求原函数进行了联姻,于是微分与积分的基情就开始了。
微积分基本定理(英语:Fundamental theorem of calculus)描述了微积分的两个主要运算──微分和积分之间的关系。
定理的第一部分,称为微积分第一基本定理,此定理表明:给定任一连续函数,可以(利用积分)构造出该函数的反导函数。这一部分定理的重要之处在于它保证了连续函数的反导函数的存在性。
定理的第二部分,称为微积分第二基本定理或牛顿-莱布尼茨公式,表明某函数的定积分可以用该函数的任意一个反导函数来计算。这一部分是微积分或数学分析中相当关键且应用很广的一个定理,因为它大大简化了定积分的计算。 #viaWikipedia
三、和约束说不(1)
第一节里提到,牛顿力学方程有些力不从心的原因在于研究对象会受到约束,所以 如何在求解问题的过程中“消除”约束就是一个刚需 。这里将“消除”加上引号,并不是说真的把作用在研究对象上的约束给解除掉,而是指在方程里不出现这些未知的、复杂的约束,从而使得方程变得更易求解。在那个小球沿圆轨道运动的例子里,咱们发现只要换一个坐标系就能使得求解变得柳暗花明又一村。
这是偶然还是必然?这背后有没有隐藏着什么不可告人的秘密?谜底揭晓,这个秘密就是坐(zou)标(jin)变(ke)换(xue)!即不再用直角坐标
不过要提醒一点的是,坐标变换没有绝对的好坏,只有在具体问题中存在相对最适用的区别。这就好比现金和手机支付一样都有存在的价值,手机没电没网的时候,现金支付是不是很香呢?
那如何进行坐标变换呢?这里有个依据—— 一个被称为自由度的东西 。对于一个自由质点来说,当其在空间运动时,由矢量分解的特点可知,需要3个直角坐标
由于每个质点都是自由的,所以这些坐标都是彼此独立的,少一个都不能把这个质点系的运动状态给描述清楚。 这些独立坐标的个数就是这个研究对象的自由度 。
但是对于受约束的研究对象来说,自由度肯定是要小一些的,因为约束的存在使得原先的部分坐标之间会有联系。还是看第一部分给出的小球沿圆轨道运动的例子,小球在竖直平面内运动,所以需要
的约束条件。
这个约束条件的存在,使得
推广开来,对于由
也就是说 描述这个受约束的系统,只需
至于新的坐标系是什么样子的,甩给你一句话—— 具体问题具体分析 !好家伙,反手就是一个好家伙。比如说可以选极坐标呀,柱坐标,球坐标等等。为了给这些新坐标起个统一的名字,就叫它们为 广义坐标 吧。
不过别高兴得太早,换坐标并没有真正做到“消除”约束。啥情况?虽然使用广义坐标后,自由度从
回想第一节里提到的约束,意思就是物体的运动状态有所被限制。比如车轮在地面上无滑动的滚动;刚体具有不变的形状;被光滑铰链链接的刚体等。这些例子里,静摩擦力就是使得车轮不滑动的约束力;刚体的内力约束其形状不变;铰链约束着被链接的刚体的运动状态。
对于纯滚动的物体来说,静摩擦力对其不做功;对于刚体来说,由于其形状不变,其内部各质点没有相对位移,所以内力做功的代数和为零;考虑铰链约束的特点,铰链上的约束力所做功的代数和也为零。这些例子透露出, 咱们可以通过从做功的角度来消除约束力的影响 。
可是做功就会涉及到位移,那物体应该发生怎样的位移才能使得约束力做的功为零呢?这样的位移是特殊值还是普遍值呢?或者说物体真能发生这样的位移吗 ?
问题发展到这里,咱们又遇到了拦路虎。再正常不过了,解决问题就是打怪升级的过程,咱们再次需要获得有力的数学武器。但这个武器并不是为解决约束问题而生的,其来头可不小呢。
四、初识变分
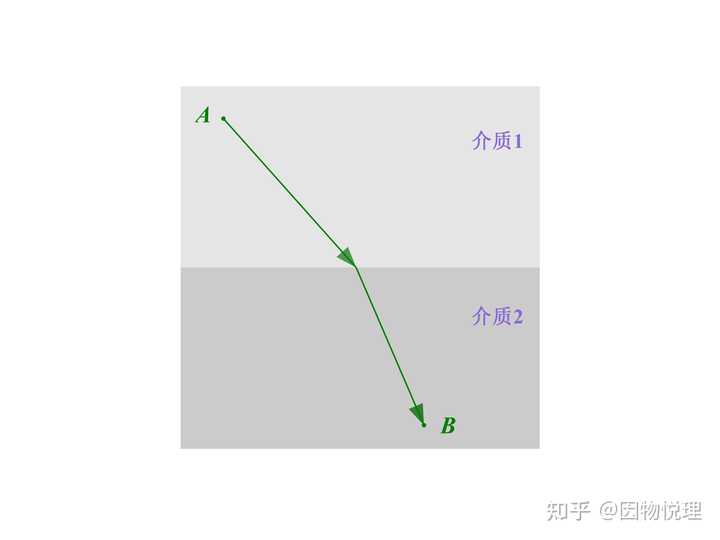
历史上有过这么几个著名的问题:光在不同介质中传播时有什么特点呢?费马断言光通过空间中固定两点的真实传播路径是其用时最短的那条路径,这便是著名的费马原理。
伯努利曾向物理同僚们踢馆,悬赏一道智力题:小球从固定高处沿某条轨道滑到固定低处,怎样的轨道能使得小球最快到达目的地呢?这便是著名的最速降线问题。

关于这两个问题的具体求解,在后面会展现出来,这里暂时只说问题的求解思路。这两个例子都是要解决同一个问题—— 要从众多可能的轨迹中选择一条确定轨迹,该轨迹对应着最小值 。
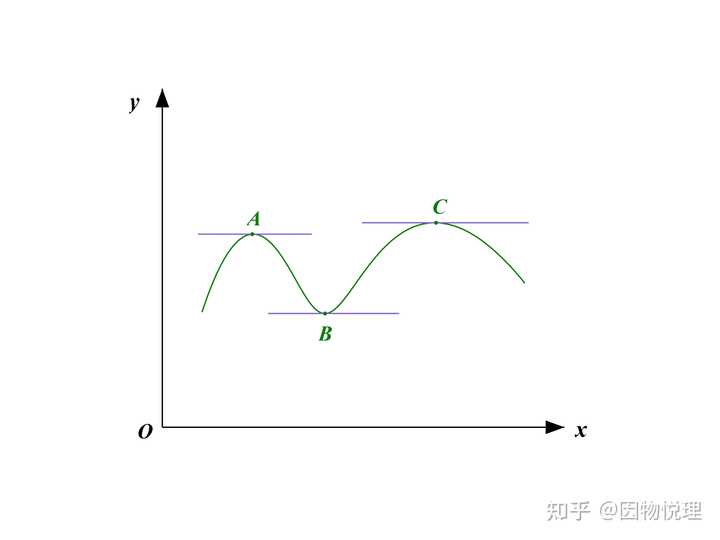
提到求最值应该不陌生吧?高中数学里不是经常求函数的最值么?所谓函数的最值,你可以想象有一片山区,所有山顶中最高的就是最大值,所有山谷中最低的就是最小值。而每个山顶(谷)称为函数的极大(小)值,所以求最值就转化成求极值。
用数学语言描述就是自变量
不过要注意的是,上述两个例子并不是要求函数的极值,而是 函数的函数取极值 的问题。啥?你确定你没多打几个字?没有!且听我娓娓道来。
求函数的极值,前提是这个函数已知了。比如咱们熟悉的抛物线函数
但是上述两个例子里,咱们事先连函数的表达式是啥都不知道 !这不显然的嘛,要是知道了函数表达式,路径不就知道了么?
所以例子里的问题应该是这样的:事先给定了
你看嘛,这不就是给函数再套一个函数嘛?所以,函数的函数这个叫法就是这么来的。拗口是吧?谁说不是呢?!所以它有一个新名字—— 泛函 。咱们习惯把函数记作
请不要被这个符号给吓到了,你可以随便用一个符号把
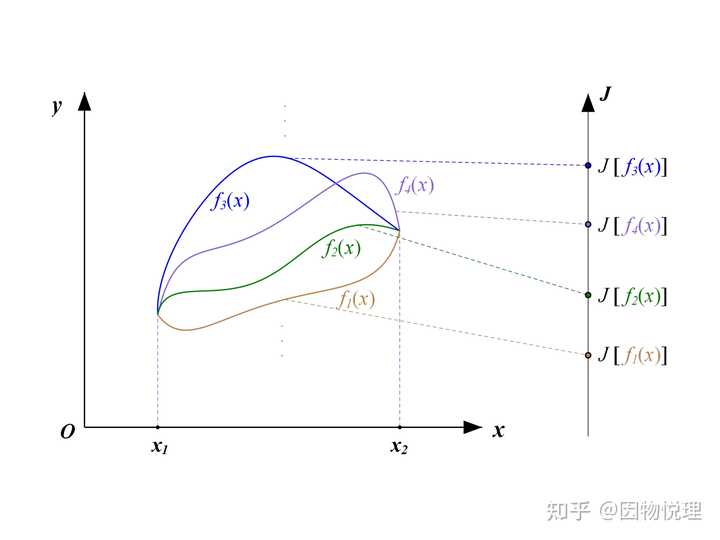 函数与泛函的区别
函数与泛函的区别
弄清楚了泛函,就可以来说泛函的极值。和求函数极值一样,也需要求出泛函的导数,然后找出它的零点。函数求导需要计算函数的变化量,同理给泛函求导也要整出它的变化量。 请再次注意泛函的变量是函数,所以泛函的变化是由不同的函数所导致的 。而这些不同的函数就引出了 变分 的概念。
当自变量
显然,泛函的变化量则为:
熟悉不?是不是和函数的变化量及其相似呀? 唯一的不同是函数的变化量来自于自变量的变化,而泛函的变化量则由函数的变分所导致 。
类比可得(此处省略了上千字的严格数学推导),泛函也有“微分”!不过为了加以区分, 泛函的“微分”称为变分 ,记作
其中
如果泛函的变量有多个,以最少的两个变量为例,则泛函写成:
则其变分为:
依据请参考前述的多元函数的微分结果。
扯点闲话,这里之所以省略了泛函变分的推导过程, 主要目的在于突出类比的思想 ,这可是物理学里及其重要的思想方法,甚至可以说是一种优秀的物理直觉! 把外在相似而内涵一致的现象归为一类,这不就是物理学的本职工作么 ?再者,泛函变分的推导远没有函数微分的推导那么直观和简洁,如果硬要堆砌出来,只会显得满满的硬核数学风,与本文的主题思想相差甚远。
言归正传,既然微分和变分如此的相似,咱们就指着相似性好好薅一下。比如说函数
再根据导数的运算法则有:
即:
也就是说对函数求变分和求导数的运算次序是可以交换的 。这个特性会在后续反复用到。
好啦,变分的神秘面纱已经被掀开了一角,咱们的武器库里又多了一项得力的数学工具。想看它大杀四方的威力还请耐心地等等,现在咱们的思绪得回到物理问题中去了。
五、和约束说不(2)
在“消除”约束的道路上,咱们发现约束力做功为零就很香,只不过会困惑于功对应的是哪一段位移,以及这样的位移有没有普遍性。哎,这讨厌的约束啥时候是个头啊?!
嗨,就这?多大点事嘛。你不是不清楚对应哪段位移么?咱就给你弄出所有可能的位移!你不是疑惑位移有没有普遍性么?咱就给你弄出所有可能的位移!你不是还.....?咱就给你弄出所有可能的位移!怎么样,管够不?
好家伙,说得容易,怎么弄呀?物体运动的时候位移是确定的,你怎么弄出所有可能的位移呢?
简单!咱不让物体真的动起来不就完了撒?此时此刻的你是不是一脸懵逼?别担心,详细解释这就附上。先说物体的实际位移,它对应着一段时间间隔,在这个时间段内,由于物体的运动已经发生了,所以这段位移也就定下来了。那要是咱只着眼于某个时刻呢? 这相当于把时间“固定”住,谁又会知道物体该往何处运动呢 ?
打个比方,当你从家去到学校,这就是你的实际位移,显然这是一段确定的位移。而你在家还没出门时,你是不是可曾想过去商场?去饭店?去球场?去一切可以去的地方?反正只要没迈开腿行动,头脑里就可以想出任何可以去的地方。
既然针对一个固定的时刻,物体在接下来的运动中可以 有很多种可能的位移 ,而这些 可能的位移并不是物体实际发生的位移 ,所以给这些可能的位移起个新名字—— 虚位移 。啊这,名字就给人一种虚无缥缈的感觉,这很物理吗?
答案是这很物理!谁说物理里只能引入那些实实在在的东西?磁感线、电场线是不是引入的两个假想工具?这里的虚位移也是如此!它的作用就好比几何题里的辅助线,背后隐藏着巨大的作用。
那么虚位移又该如何来表示呢?物体的位置咱们可以用 位矢 来表示,其实就是从坐标原点指向物体所在的位置坐标的有向线段。
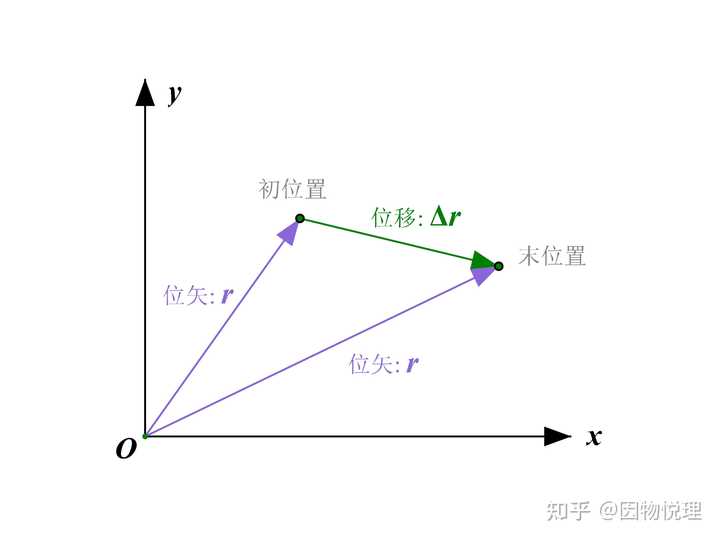 位矢与位移的关系
位矢与位移的关系
显然位矢是时间的函数,因为不同时刻物体所处的位置不一样,故把位矢记作
写到这里,大家想到了什么?这不和刚刚介绍的泛函很像么? 所以虚位移就是在固定时刻
这就是为啥咱要先初识变分的原因,因为只有当你初步了解了啥是变分,你才能明白虚位移是个啥玩意。
顺便说一下,物体的实际位移应该表示为:
由于咱们把位矢
对了,聊了这么久的虚位移,咱们可不要忘了引入它的初衷。虽然它能解决我们对于位移的那些困惑,但是最重要的问题——约束力做功为零的目的能实现吗?敲黑板啦,快点看过来。
比如物体被约束在一个光滑曲面上运动,咱们把这个曲面的方程形式记为:
如果
现在咱们让时间
成立。这不废话嘛,毕竟物体始终受到约束,就算产生了虚位移也是被束缚着,当然要满足这个约束曲面的方程撒。把这两个方程相减,你就会发现:
依据请参考多元泛函的微分。
请问有没有人觉得少一项
如果你对向量的数量积有所了解的话,上面的满足条件可以立刻改写成两个向量的数量积,即:
两个向量的数量积为零意味着这两个向量互相垂直,而这个等式里的第一个向量即为虚位移
得出了虚位移方向与约束曲面的法向量垂直的结论有啥用呢?别忘了物体在光滑曲面上受到的约束力就是垂直于曲面的弹力
哈哈哈哈,约束力终于给“消除”啦!这里出现的
再比如说刚体,其内力约束着自身形状不变,这就意味着内部任意两个质点之间的距离是不变的。假设某两个质点的位矢分别为
这个等式就是两点之间的距离公式,其中
根据前面已经推出的虚位移所满足的条件,即有:
化个简就能得到:
先别急着担忧这个化简的结果如何解释,咱们还没说这两质点所受的约束力呢。显然,它俩之间的相互作用力就是约束力。 既然是它俩之间的相互作用力,不得有等大、反向、沿着两点的连线这三个特点么 ?
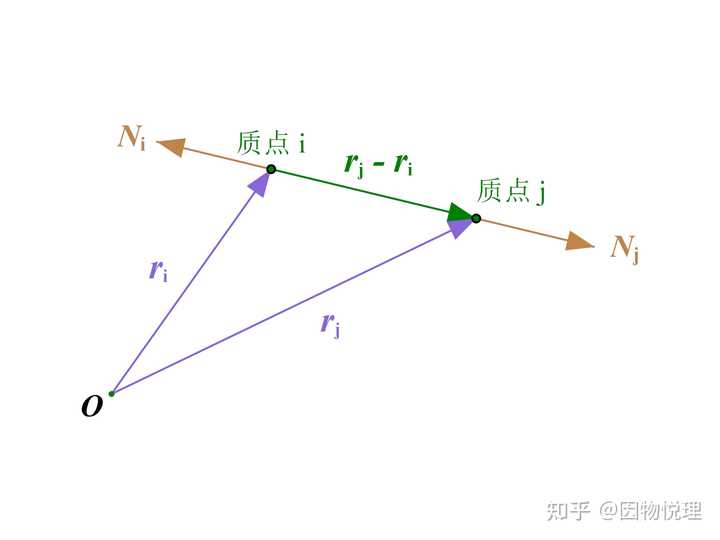
示意图里已经清楚地标出来了。如果把这三个特点的文字描述转化为数学语言,你会发现有:
前一个等号体现了两个作用力等大与反向的特点,第二个等号体现了两个力沿着两点连线的特点 。啧啧啧,你不得不称赞数学语言的精准与简洁!
接下来就该把两质点各自所受约束力的虚功给弄出来了,显然有:
和
虽然各个约束力的功不为零,但是总功:
你看,约束力依旧被“消除”了。
咋样,用虚位移“消除”约束力很香吧?而且不仅光滑支持面和刚体有这样的特点,像光滑铰链呀、绷紧且不可伸长的轻绳等产生的约束,都有约束力的总虚功为零的特点。 这就爽歪歪了,此法不仅实用,而且还能惠及一大批约束!就好比玩着消消乐,点开一个技能包消除了满屏的图案,爽不?
既然有这么多约束力的总虚功为零,于是乎就归个类吧—— 约束力总虚功为零的约束称为理想约束 ,记作:
什么,你又给我谈理想?难道物理离开了理想就不能活了?
看来有必要再次重申理想的意义—— 抓主要因素而忽略次要因素,从而把各种实际问题抽象成一个个物理模型,通过研究物理模型从而找出背后隐藏的规律 。这才是理想的根本目的!至于如何抹去理想和现实之间的差距,待你弄清了本质规律后可以慢慢加入各种实际的因素,规律的适用范围不就扩大了么?还有问题?
好啦,现在工具都已齐活,咱们即将开始大干一场!在撸起袖子之前,我想强调的是: 相比知道怎么干,弄清为什么要干和为什么要这么干是更重要的前提 !毕竟事出有因, 如果你只盯着做事之方而忽视了谋事之略,岂不是很容易堕云雾中 ?倘若读者能从这些文字中领悟到物理绝不是天马行空的胡思乱想,而是在解决一个个具体问题中逐渐发展的优美体系,我辛苦敲字的付出也就值得啦。
六、横空出世的拉格朗日方程
开工之前再强调一遍,接下来的工作只是去改造牛顿运动定律的核心方程:
让其能更好地用于有约束的场景。至于会有啥不同凡响的结果,那就拭目以待吧。
核心方程里的力
这里有
看到这个方程,相信大伙不难想到接下来要干嘛——把等式两边同时乘以对应质点的虚位移,利用理想约束的总虚功为零的特点将约束给“消除”掉。不过有个问题咱们得交待清楚:等式右边的
所以咱们要把这个方程进行一个骚操作——把
那么
各位请稍安勿躁,就是这么一个简单的移项还就真的解决了名分问题!从数学的角度来说确实就是简单的移项,但是考虑到物理量纲可就意义重大了。咱看个通俗易懂的例子,假设一份饭20元,可以写成等式:“20元=一份饭”。你若没有一张20元的钞票,可以付两张10元的钞票嘛,那么等式为:“10元+10元=一份饭”。 也就是说钱和钱能直接相加,可你有听过钱和饭相加的吗 ?即 对于物理量来说,只有量纲相同的量才能相加 。倘若你非要把等式里的“一份饭”进行移项,将其写成:“-(一份饭)+20元=0”, 那么“-(一份饭)”表示的只能是钱!只能是钱!是钱! 看到这,你还觉得移项是个简单的活吗?
回到牛顿第二定律的方程里来,
里的每一项都有了正当的名分,分别是惯性力、主动力和约束力。若将等式两边同乘以质点
那么各项分别是惯性力的虚功、主动力的虚功和约束力的虚功。
如果这个质点系受到的是理想约束,不就有约束力的总虚功为零么?也就是:
所以咱们只需把所有质点的虚功方程相加即可构造出约束力的总虚功,即:
于是对于理想约束的体系来说,改造后的方程就能简化成:
等等,你管这个叫简化?我的拳头都变硬了!
相比单个不受约束的质点的方程来说,上式确实有些复杂,那是因为单个不受约束的质点本来就是最简单的情形啊。但是对于受约束的体系来说,上面的方程成功地消除了未知约束力的影响,你能说它不是简化的结果?
另外咱要坦白的是,上面的简化结果是借助理想约束的条件才得到,可是在复杂的现实面前,理想化岂不是我们的一厢情愿吗?并不是的! 遇到非理想约束的情形时,你把力
理想化的问题咱们可以不纠结了,但是这个简化方程里又出现了一个新的问题——虚位移。 物理规律建立在这么一个虚无缥缈的对象之上,总让人觉得不放心,所以社会主义改造的步伐依然不能停下来 。
咱们回头看看得到的方程,它是
果真如此的话,这个方程就退化成了自由质点的牛顿第二定律表达式啦,说明上面的这个简化方程是可以包含无约束的简单情形。而对于有约束的质点系来说,质点系的虚位移之间不再是彼此独立的,怎么办?
想起来了吗? 在第三节里面就提出了专门解决这个问题的办法——广义坐标 呀。假设这个受约束的质点系的自由度为
那么每个质点在时刻
这里有
质点的位矢被广义坐标给表示出来了,那么质点的虚位移肯定也就不在话下了撒。显然有:
注意虚位移的特点,时间是被固定的。所以把上面两式相减,再参考多元函数的微分就有:
这么写挺麻烦的,甩出求和符号就挺简洁,即:
更换了广义坐标后,方程就变成了:
大伙千万不要怕这个表达式,这就是把
的表达式相加而已。
另外,根据速度定义可知,速度等于位移除以时间,也就是位矢对时间的导数;而加速度是速度的变化量除以时间,也就是速度对时间的导数。所以加速度就是位矢对时间的二阶导数( 数学部分涉及导数时,约定在函数字母的右上角加撇号;物理部分涉及导数时,约定在物理量字母的头上加点号 ),记为:
最终方程变为:
把等式左边的这一坨东西稍微变形一下(即把小括号拆开),就变成了:
眼瞅着等式越写越长,这还了得?那就先找个新符号吧,令:
称其为 广义力 。
这个叫法很自然,因为方程的第一项变为了:
对比原始方程就会发现这不就是广义坐标下的“主动力”的虚功么?所以把
等等,我咋感觉你又在敷衍呢?说来说去,你只不过是换了壳,用
现在重点说说等式里的第二项,只要咱们稍微施加一下魔法就可以让它大变样!由于这一项里存在二阶导数,如果咱们想要求出未知的位矢,那么需要积分两次才能还原。本来积分计算就比较麻烦了,结果还要来两次,岂不是自讨苦吃?难道就没啥好的法子吗?
有的亲, 分部积分法 就能大有作为。所谓分部积分法其实就是利用两个函数乘积的求导公式来替换积分对象,从而使得积分计算变得相对容易。所以,为了替换掉这个讨厌的二阶导数,咱们将其变换为:
别怕别怕,动手把等式右边的第一项按照函数乘积的求导法则展开就能得到上述这个恒等式,要不亲自试试?
这么一弄,二阶导数就可以被替换了。可是替换出来的结果里变成了两项相减,而且看起来挺吓人。别急,魔法还没施展完呢。
由于
而
来个求和符号,并且把 广义坐标对时间的导数即广义速度 记为其字母的上面打一点,于是有:
顺带着咱们还发现了这么一个结论:
因为你是把
再来看
这一项。
所以考虑一般情形下,将
显然我们得用上求和符号的,则有:
请注意是角标
嘿,你想退出不看了吗?哎,我说别急着走呀,上式不就是多元函数的求导嘛?看把你给吓的,别怕哈。况且好戏马上就要开始了,不信的话继续往后看。 由于每个广义坐标是彼此独立的,所以可以把求导的先后顺序进行调换 。为啥要这么做呢?话不多说,先看看效果吧:
看出变化了吗?求导顺序调换后,就是把对
这下你明白了交换求导顺序的目的了吧?对了,这出戏还算精彩不?偷偷告诉你,后面的好戏更多哟。
写了这么多公式,其实就是把
再把等式右边第一项的求和符号放到求导运算里,则:
这回看起来是不是有特点了?因为等式右侧的两项里都含有
还记得复合函数求导的法则吗?如果复合函数长这样:
那么函数
和
这两个结果刚好就能和等式右侧的第一项与第二项对上。巧不巧?
是不是有点好奇为啥会选择函数
对了,你看
倘若你亲自演算一下就会发现:
怎么样,世界是不是一下子就清爽了很多?
如果再把之前定义的广义力翻出来,咱们花费了一些精力改造的牛顿第二定律表达式就变成了:
由于每个广义坐标是彼此独立的,要使所有项的和为零,只能是:
这里有
好端端的牛顿第二定律表达式被你整成这幅模样,这是整形失败了?别急着吐槽,人家这个等式其实长得也不差,至少也很简洁,不是么? 况且我们在改造之前就说过两个目的:其一是为了解决未知的约束问题,其二是为了避免使用矢量式 。你看它是不是都解决了?至于能否把它熟练地用得飞起,就看你的数学水平了。
当然了,大佬们也想面对简单问题,所以把目光瞄向了广义力。对于一类被称为 保守力 的力来说,它们共同的特点是: 对物体做的功与物体的运动路径无关,只与物体的起止位置有关 。这句话一说出来,是不是立刻想到了好几种这样的力?重力、弹力、静电力、分子间的作用力。既然这些力做功有如此特点,它们就会对应着相应的势能:重力势能、弹性势能、电势能、分子势能,是不是个个都耳熟能详?
咱们就拿最简单的重力来说吧。高中物理里,重力做功与重力势能变化之间的关系很简洁:
也就是说,重力可以表示为:
对于质量不变的物体来说,其受到的重力是恒定的(不考虑高度和纬度变化带来的微小影响)。所以咱们可以利用上式计算出整个过程里物体在任意位置的重力。那么问题来了,换成一个变化的力,比如弹力、非恒定的电场力,又该如何求出物体在某处所受的保守力呢?
这个问题是不是似曾相识呀?祭出极限大法不就可以了么?咱让初末两位置无限接近,极限情况下,上述的比值不就是物体在某处所受的保守力么?等式:
蹦蹦跳跳地向你招手。
等等,这不就是重力势能对高度的导数么?即:
同理,弹力与弹性势能之间、电场力与电势能之间都有类似的关系,有兴趣就自己去推理吧。咱们就统一把势能记为
可能有读者会疑惑这里为啥是偏导,而刚才重力的表达式里却是导数。很简单,重力势能只与竖直高度有关(重物不变),所以重力势能是位置(竖直方向)的单变量函数。而一般情形下,势能是位置分量的多变量函数。
另外,如果你想直接写出保守力矢量与势能的关系,就得写成:
因为势能对位矢求偏导,其实就是分别对它的三个直角坐标分量求偏导,结果依旧是矢量,即:
而力不就是:
稍微推广一下,对于含有
这里有
有了这些铺垫,广义力:
就可以拿来改造了。求和符号里是两个矢量的数量积,咱们把它俩改成坐标形式,即:
接下来就是向量数量积的坐标运算啦,咱就不多费口舌了,结果为:
等式右边的这一坨东西连同求和符号一起,恰好就是
对比“普通力”和势能之间的关系,你会发现两个等式的形式及其相似。从这个角度来说,把它称为广义力也是名副其实呀。
把这种简单的结果带入到之前的方程里,就有:
由于势能一般只是位置的函数,与速度或者广义速度无关,说明:
所以可以把等式右边第一项里添一个零项,使得方程的形式变得更加简洁,即:
如果你嫌书写太麻烦,可以令:
则有:
这就是大名鼎鼎的拉格朗日方程,
拉格朗日方程(Lagrange equation),因数学物理学家约瑟夫·拉格朗日而命名,是分析力学的重要方程,可以用来描述物体的运动,特别适用于理论物理的研究。拉格朗日方程的功能相当于牛顿力学中的牛顿第二定律
假设一个物理系统符合完整系统的要求,即所有广义坐标都互相独立,则拉格朗日方程成立: #viaWikipedia
完整系統: 在經典力學裏,假若一個系統的所有的約束條件都是完整約束,則稱此系統為完整系統(holonomic system)
咱们回想初衷,不就是希望把牛顿第二定律变得好用一点么?心高气傲的拉格朗日才不会满足于小打小闹地数学技巧,他要的是站在巨人肩膀上开宗立派,发展出能一劳永逸解决力学问题的根本方法。 这就好比战场杀敌,弱时小米步枪战术穿插,强时飞机大炮给老子炸!火力强就是王道 !

这里咱们承认拉氏方程的根本性,原因之一是无论广义坐标怎么取,拉格朗日方程都是不变的,这种万变不离其宗的魅力谁能抵挡?至于它是否还具有更深层次的意义,有待后文揭晓。
在即将结束此节内容之际,咱还得回答读者心中可能的一个疑惑:美如诗的拉格朗日方程是在保守力的前提得出的,那么问题就来了,保守力虽有,难道所有的力都是保守力?起码咱们熟知的摩擦力可不是保守力!这怎么搞?
假設一個受到某作用力的粒子,從初始位置移動到終結位置,而此作用力所做的功跟移動路徑無關,則稱此力為保守力(conservative force),又稱為守恆力,等價地說,假設一個粒子從某位置,移動經過一條閉合路徑後,又回到原本位置,則作用於這粒子的保守力所做的機械功(保守力對於整個閉合路徑的積分)等於零 #viaWikipedia
假設在一個物理系統裏,所有的作用力都是保守力,則稱此物理系統為「保守系統」,又稱為「守恆系統」
對於這種系統,在空間裏每一個位置,都可以給定位勢一個唯一數值。假設粒子從某位置移動至另一位置,則由於保守力的作用,粒子的勢能可能會有所改變,但前後差值與移動經過的路徑無關。例如,重力是一種保守力,而摩擦力是一種非保守力
你得这么看: 从本质上摩擦力是电磁力,而电磁力属于保守力 。所以拉格朗日方程似乎不会遇到非保守力的情形。不过这是从微观层面来说的,可是在宏观层面摩擦力是真实存在的,而且也不是保守力,此时咱们得到的拉格朗日方程就不能把广义力那一项进一步化简了。至于计算起来会不会很头铁,机智的我再次甩锅给数学了哈。
七、费马原理和最速降线
在揭示拉格朗日方程的深刻内涵之前,咱们得把目光转移到拉格朗日之前的时代。因为在此之前,有两个不同问题的答案殊途同归,冥冥之中好像暗示着什么。
前面已经提到过费马原理和最速降线问题,现在咱们要正儿八经地写出方程进行求解了。咱们都知道光在介质中的传播速度满足:
为了使讨论一般化,在光线穿过的平面区域内,介质的折射率
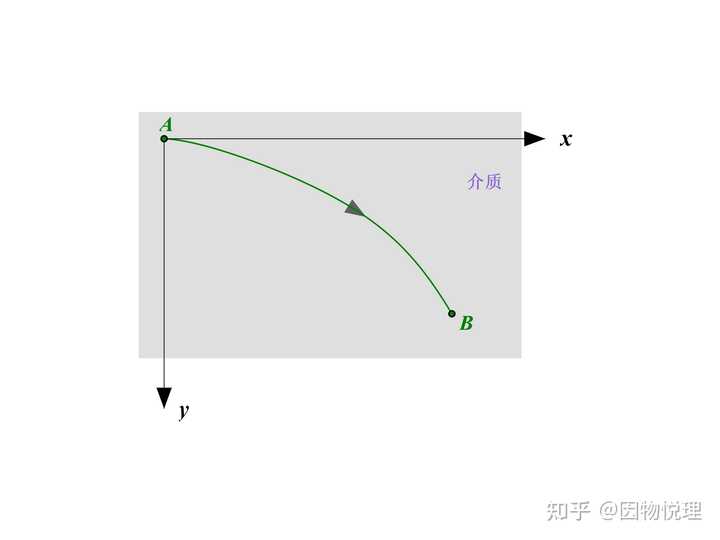
如今咱们想计算出光从一点传播到另一点的时间,不就是路程除以传播速度的事嘛,考虑到传播速度是变化的,微积分拿去用,不谢哈。所以咱们得先计算光通过的一小段路程,有:
然后算出通过这一小段路程的时间为:
最后算出通过全段路程的时间为:
费马原理说光在介质中通过固定两点时,是沿着传播时间最短的路径行进的。 所以咱们现在的任务就是要找到一个路径函数
而最速降线问题与之类似。
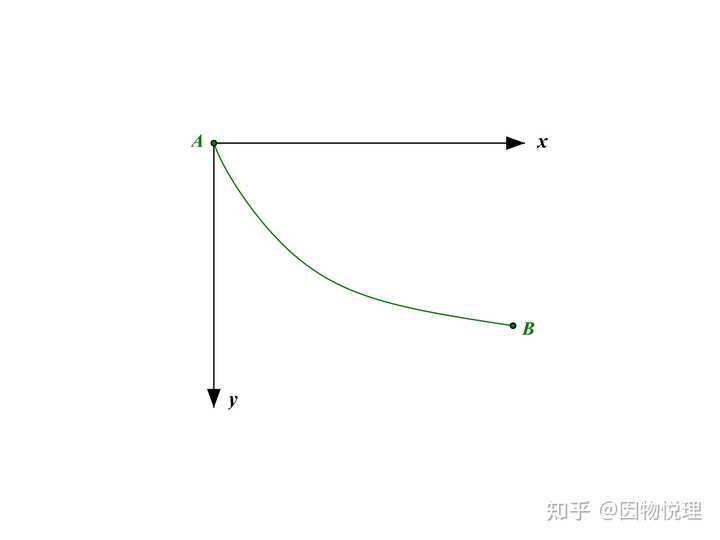
咱们先算出小球经过的一小段路程:
再根据机械能守恒定律,可以求出小球下降高度为
可得:
所以小球通过这一小段路程的时间为:
显然,小球通过全段路程的时间为:
不难看出, 最速降线问题目的也是要在两端固定的区间里找到一个路径函数
其中泛函
要算泛函的导数,也就是计算泛函的变分
所以咱们得先从此处入手。这里的
接着,咱们就引入一个变量
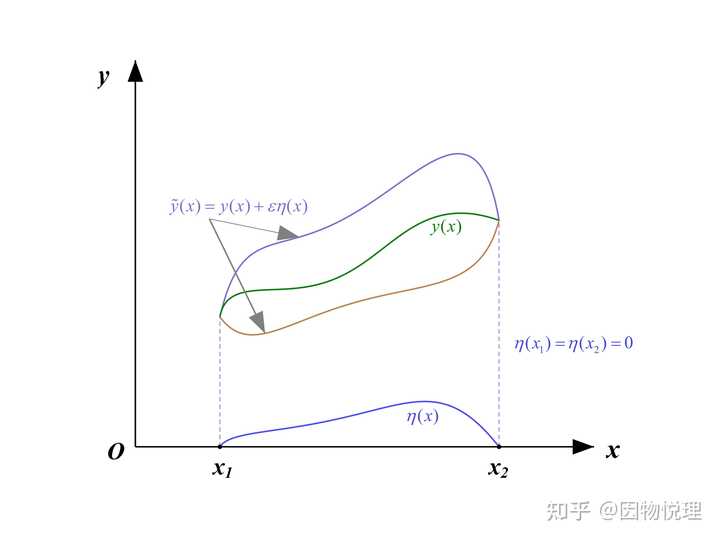
这里只要求
而
有点迷惑不?明明
请听好,是这样理解的:咱们是事先任选一个函数
这么处理的好处是可以把泛函
是参数
也是如此。
那么把泛函
如此一来,泛函
求导的链式法则还不用起来?显然有:
之所以写成
刚才咱们在写
时才有:
所以这就要求
和
另外,根据
和
两式,有:
和
好啦,万事俱备,咱就开始吹东风吧。目标导数就写成:
为了利用两端处
接下来只需对上式两边积分:
等式右侧的第一项就为零了,因为
最终,咱们的目标导数就变成这样了:
由于
而
这里稍微多说几句,假若被积函数
并且所有函数取值的端点也是固定的。那么只需完全复用上面的推导过程,则有:
不要怕嘛,相比只有一个变量的情况来说,多个变量的情形无非就是在求导时熟练使用链式法则。
那么对于每个独立的变量
所以上面那个繁琐的等式里,右边的第一项为零了。再根据:
的结果以及每个
卧槽, 这个结果的形式与上一节得出的拉格朗日方程如出一辙!如果把上式里的
咱们捋一捋,最速降线问题在欧拉时代(1728年)就利用变分法(从几何的角度)得到了完美地解决,但若干年后(1755年)的拉格朗日提出了更普遍的方法——从分析的角度利用变分法,并严格得出了上述方程。咱们刚才的推导思路就是拉格朗日对变分法发展的贡献,此乃拉神的成名作!而为了解决含有约束的力学问题而诞生的拉格朗日方程是之后的事了(1788年)。
试想一下你是当年的拉神,当你看到自己全新改造的力学方程竟然有早已在世且失散多年的孪生兄弟,你会不会去重新审视变分法和力学方程之间的关系呢?所谓老树开新花,像这种老方法应用到新问题并得出新结论的故事即将上演。
八、最小作用量的前世今生
现在咱们的思绪又得重新回到费马时代,他和一批批学者一样是简洁的拥趸—— 自然界本身就是简洁的亦或是描述自然界的理论是简洁的,总之简洁就是王道 。在这种信仰的加持下,他必然想要提出一个能解释多种光现象的理论,于是他认准了光在传播过程中走时间最短的路径。
想知道这个原理是如何来解释光的传播特点的吗?不要走开哈。
我们知道光在同一种介质中传播时是沿直线传播的。由于两点之间线段最短,而光在同种介质中的传播速度是定值,所以光沿着这条最短路径传播用时最短。
再来看光的反射现象,它指的是光从一种介质射到与另一种介质的分界面时,一部分光会返回到原介质中的现象。即整个过程里,光始终在同一介质中传播,所以传播的速度是定值。显然,当整个光路的长度最短时对应的传播时间最短。从下图中可以看到,依然是两点之间线段最短的特点。
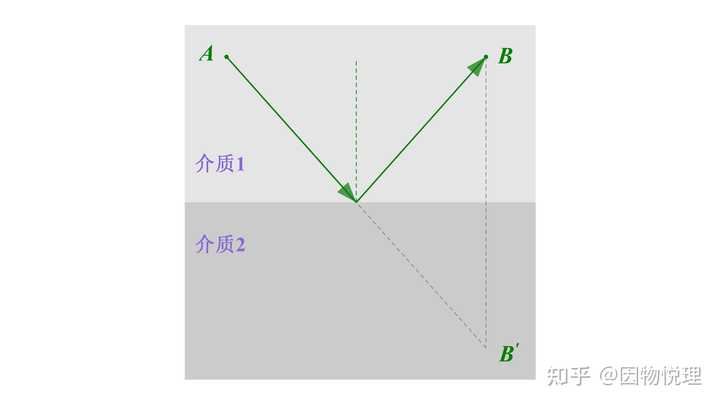
最后再来看光的折射现象,它指的是光从一种介质射到与另一种介质的分界面时,一部分光会进入到另一种介质中的现象。由于光在不同介质中传播,所以传播的速度会发生变化。显然这种情况下,路程最短对应的时间就不是最短的了。
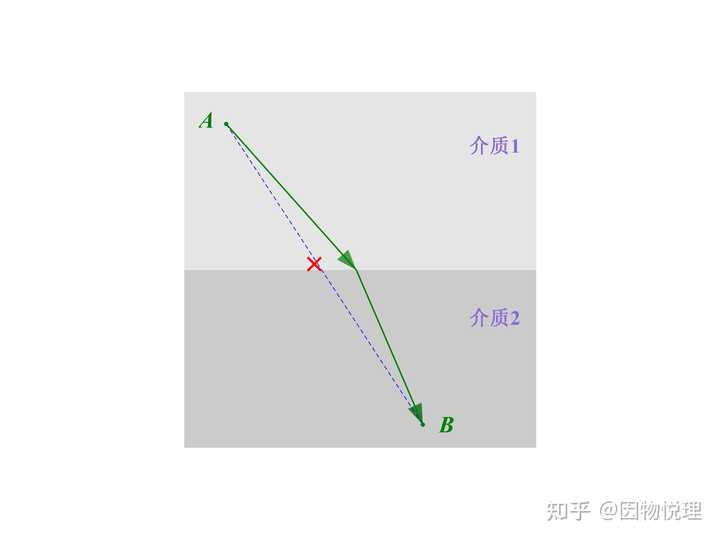
因为你得让光在传播速度快的介质里多走一段路程,而在传播速度慢的介质里少走一段路程,这样才能使得总时间最短。至于折射点在哪,费马自有他的方法给确定出来。这些细节不是这里的重点,咱也就写个批注吧:“ 我想到了一个绝妙的办法来找出折射点,只是这里的空白处太小,写不下了 ”。毕竟咱等凡人学不来费大神的成就,他的骚操作总可以学学吧?
可惜咱们被费大神撩得刚要入迷就被一盆冷水给泼醒了,因为费马原理虽然可以对光的传播特点做统一解释,可是面对光的干涉或者衍射现象就无能为力了。而且不怪咱们事后诸葛,这个原理本就有很大部分的先验假设,你可以认为是费马的物理直觉或信仰的体现。况且当时也没有合适的数学工具对其进行严格证明,所以这一次费马对简洁地追求算不上成功。但是前人栽树后人乘凉,费大神的思想星火吸引着后来人助其燎原。
在发展费马原理的人群中,绝对绕不开被称为最小原理之父的莫培督了。他认可费马的思想,但是想不通光的传播路径为啥是从耗时最短和路径最短中二选一。于是他来了个新瓶装旧酒——光所钦定的路径,其真正优势在于作用量最小!
最小作用量原理 - Wikiwand 在物理學裡, 最小作用量原理(英語:least action principle),或更精確地,平穩作用量原理(英語:stationary action principle),是一種變分原理,當應用於一個機械系統的作用量時,可以得到此機械系統的運動方程式。這原理的研究引導出經典力學的拉格朗日表述和哈密頓表述的發展。卡爾·雅可比特稱最小作用量原理為分析力學之母 #viaWikipedia
在現代物理學裏,這原理非常重要,在相對論、量子力學、量子場論裏,都有廣泛的用途。在現代數學裏,這原理是莫爾斯理論的研究焦點
最小作用量原理有很多種例子,主要的例子是莫佩爾蒂原理(Maupertuis' principle)和哈密頓原理
费马的表述
费马原理,又称为“最短时间原理”:光缐移动的路径是需时最少的路径
莫佩尔蒂的表述
莫佩尔蒂发表的最小作用量原理阐明,对于所有的自然现象,作用量趋向于最小值。他定义一个运动中的物体的作用量为𝐴,物体质量𝑚、移动速度𝑣与移动距离𝑠的乘积,莫佩尔蒂又从宇宙论的观点来论述,最小作用量好像是一种经济原理。在经济学里,大概就是精省资源的意思
欧拉的表述
欧拉在论文《寻找具有极大值或极小值性质的曲缐,等周问题的最广义解答》里,以非常清楚的字句,给出最小作用量原理的定义
採用现代术语,这积分等于简略作用量 ∫ 𝑝 ⋅ d 𝑞 其中 𝑝 是广义动量, 𝑞 是广义坐标
至于作用量是啥,莫培督给出的答案是质量、速度和所通过的距离三者之积。至于他为什么要这么定义,鬼知道!这不就留下把柄了么?马赫作为代表就曾严厉批评,说莫培督的最小作用量原理只是一个模糊不清的概念,勉强地被用来解释各种不同的物理现象。想象一下你看着答案去凑解答步骤,是不是有内味了?
虽然莫培督的最小作用量被不少人诟病,但是它确实尽到了去统一解释不同物理现象的使命,比如不仅解释得了光的折射定律,还驾驭了碰撞过程中的动量守恒定律。这给追求简洁的执念喂的饼还不够大吗?虽然这个饼有点夹生,好在神队友欧拉来操刀了。
欧拉在研究静力学的平衡问题时就独立发现这类问题的特性都可以用某个量取极小值而导出。这下可就激发了欧拉的探索欲望,他想得到描述力学问题的普遍方程。好一个透过现象看本质,要知道欧拉可是解决了最速降线问题的大神,变分法就是由他创立的,人家的实力可是明摆着呢。
他修改了莫培督的最小作用量原理的表述:设定一个质量为
你说的修改表述就是加了一个积分吗?你要这样想可就图样图森破了。 欧拉是要用变分的思想找出任意可能路径中的某一条路径,而这条路径对应的作用量取最小值 。从数学上来看,这是一个泛函问题。而莫培督的表述其实就是一个函数极值问题,即他已经知道了实际轨迹,然后用他定义的作用量一算,唉,发现其取最小值。 这就好比欧拉是正向写出解答过程求答案,而莫培督是知道答案反过来给出解释 。这才是欧拉表述的精髓所在,况且人家还自带严格的数学工具做后盾。
咱们弄两个例子来体验一下这个表述的威力吧。先看最简单的情形,如果没有任何外力作用在一个运动的质点上,根据牛顿第一定律可知,这个质点做匀速直线运动。那么从作用量的角度来看,如何得出这个结论呢?
由于质点的质量不变,当其不受外力时,其运动的速度也不会发生变化(加速度为零)。对于作用量
再来看抛体运动。质量为
这里的
那就试试作用量吧。首先写出运动过程中的小段弧长:
所以作用量为:
利用前面介绍的求变分导数的办法就能找到令作用量取最小值的条件,由此就可以求出
欧拉虽然有理有据地论证了最小作用量的观点,但是没有力学方程的背书让此观点依旧显得有些神秘。不过欧拉的成功尝试让拉格朗日看到了曙光,于是乎,拉神拿起了有自主知识产权的变分法武器去攻打最小作用量这个高地。
咱们在前面为了解决约束问题,通过引入虚位移的办法成功改造了牛顿第二定律,得到了被称为动力学普遍方程的结果:
由它出发,一路斩荆披棘得到了拉格朗日方程,从而可以求得物体的运动轨迹。而拉格朗日早在解决数学里的泛函极值时就利用变分法得到了相同的方程,因此很难不联想到用变分法求作用量的极值也能求得物体的运动轨迹。探索就是从改造动力学普遍方程开始的, 前方高能预警 !
首先把方程移项成:
再把加速度写成位矢的二阶导数。显然咱们是讨厌处理二阶导数的,所以分部积分法刚好可以麻溜地用在等式右侧的这一项上:
考虑到约束问题的自由度,所以方程得改用广义坐标,那么下面的几段文字纯粹是数学运算了,各位看官请保重。
先看
在第六节里已经出现过很多结论,咱们这里就照搬啦。各位要是忘记了,请辛苦回头查阅哈。显然有:
所以有:
求导的链式法则用了那么多次,你或多或少应该有些敏感了吧?你瞧上式的括号里出现了
倘若
映入了咱的脑海。
我在这里之所以略显啰嗦,是希望读者明白数学证明也好、数学推导也罢,并不是毫无目的的演算,而是顺着逻辑线自然发展的。所以读者不要被这种略显繁琐的推导给吓到了。
这下可好了,于是就有:
请注意“一点”之差 !你瞧
所以有:
于是咱们就将
是不是看得还算过瘾且轻松呢?
接着看第二项:
而右边的结果就是
对了,原方程里的
你若换成广义坐标,那就是:
这个结论也早就在第六节得出了。所以不管你是用啥坐标体系,这一项就是主动力的虚功,就算天王老子来了也变不了。
好了,来看看动力学普遍方程的整形结果吧:
既然整过形,咱们就称其为动力学普遍方程的1.0版本吧。哎,大夫,还能帮我把这儿给整整那儿给修修不?咱还想再简化一点。 行,那就满(得)足(加)你(钱) !
上式左侧的括号里不是有
另外,如果主动力是保守力,那么保守力的虚功就有对应的势能
要是物体运动过程里还存在着机械能守恒的特点 ,那么物体的动能与势能之和就是一个定值,即:
经过这么一番精心打扮后,动力学普遍方程被简化成:
撒花,2.0版本的动力学普遍方程发版啦!高能预警暂告一段落,果断给自己加个鸡腿吧,能看到这里实属不易!
享受完美食地犒劳,咱们又得继续开工啦,毕竟唯美食和知识不可负也。各位在刚才的数学变换中有没有忘记最初的目标呢?咱们可不是吃饱了没事干就跑来给动力学普遍方程做个整形,咱们是希望借助这个方程撑腰去坐实最小作用量原理。所以咱们得紧盯作用量不放手。
说到这,估计大家和我一样一脸懵逼——作用量到底是个啥? 其实作用量就是人为定义的一个东西,现在有了动力学普遍方程和严谨的变分学做后援,咱们要做的就是把它给“凑出来” !是的,你没看错,就是给“凑出来”。所以接下来的内容数学味颇浓而物理色彩有些黯淡, 警报拉响 !
回想上一节得出拉格朗日方程的经过,咱们的目标泛函形如:
当泛函的变分
恰好等式右侧的这一项里有变分符号,若将其拿到积分符号外侧,作用量会不会就构造好了?
呃,我有句话不知当讲不当讲:上述积分有一个非常隐蔽的bug。什么?!你看呀,在目标泛函
里,咱们是要求所有可能函数的自变量都在
可是咱们在得出
的时候假设了物体在运动过程中机械能守恒,这不bug就出现了: 所有可能路径的起止位置一样(这是大前提)、现在又要求所有路径对应的起止时刻也相同、你还假设所有路径都有机械能守恒的特点,你觉得这么多要求加一起是不是可以直接报出这条轨迹的名字了 ?这哪还需要对作用量求变分呢?
所以, 在所有可能路径的起止位置一样、又想利用机械能守恒的特点,那么就意味着所有可能路径的起止时刻必然不同 。咱们现在必须重新审视函数的变分了,深呼吸一下, 警报再次拉响 !
当每条路径对应的起止时刻不同时,路径函数的变分还要考虑到时刻不同所带来的影响。按照第四节所叙述的函数变分记为:
将
此处的
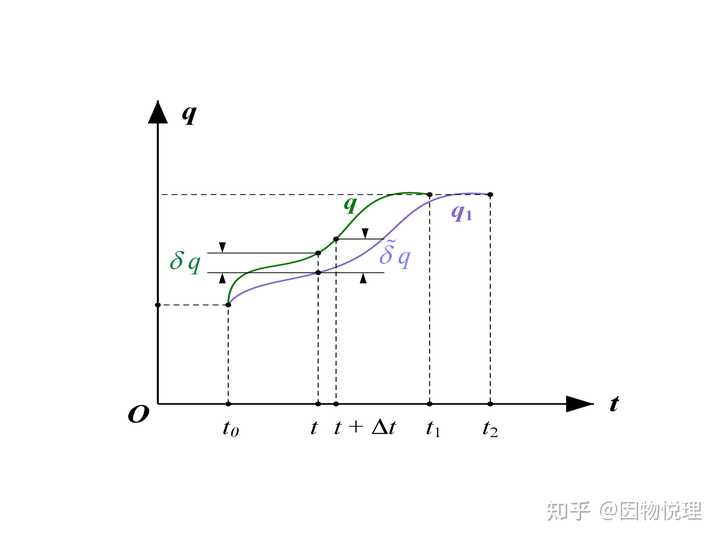
等时变分与非等时变分的区别
参考一元函数的微分可得:
将其带入到非等时变分的式子可得:
显然,等式可变为:
将得到的
上式左侧的结果是现成的,即:
而改造的重心就在右侧的第二项,没别的,就是眼熟。谁让右侧第一项里含有非等时变分呢,咱以前从没弄过撒。
现在目光锁定在了
我猜你可能不习惯求动能对广义速度的偏导,没关系,咱把坐标换回去就完事了。(此处的推导方法不唯一,下面的推导过程就当抛砖引玉了)
咋把坐标换回去呢?还是求导的链式法则撒,只不过这回是反着用,不信你看结果:
没毛病吧?只是这越写越长的式子看得人心里发毛,当务之急是赶紧给它整形。
由于位矢和广义坐标之间的函数关系本就未知,所以
则整形的第一步就变为:
由于第一个求和符号只对最后两项有作用,所以结果可以改写成:
嘿,看到
倘若你要求位矢的导数, 二营长,你的链式法则呢?给老子上啊 !于是有:
咋还多了
如此,咱们的整形手术就可以完工了,有:
等号右侧的结果完全就可以直接看出来了:
也就是咱们发现:
好啦,众神归位,方程
就变成了:
由于
你看右侧的部分是不是刚好就是动能
对比2.0版本的动力学普遍方程
咱们现在就可以放心地对打了补丁的2.0版方程两边进行积分了,有:
对于不同的可能路径,其对应的起止时刻
显然等式左边的积分结果为:
因为虽然每条可能路径的起止时刻不同,但大前提是每条可能路径的起止位置是一样的,所以在两个端点处有:
于是乎就有了拉格朗日心心念的最小作用量啦,即:
也就是说拉格朗日要找的作用量为:
当它的变分为零时就能推导出力学中的拉格朗日方程啦!
奇怪,当初从力学问题中得出的拉格朗日方程明明长这样:
可是你这作用量里没有拉格朗日函数
对了,咱们不是一直假设有机械能守恒的特点么?所以
好啦, 警报彻底停歇 了。回想这一路的历程,咱们发现猜想终归只是猜想,无论你有多么坚定的信念也必须付之严格的证明,这颇有一番西天取经之意境。如今终达极乐世界,想必曾经的艰辛也是值得的。不过我佛讲究九九归真,劫数未满难成正果,拉格朗日推出的最小作用量原理便是如此。
究其原因就是这个最简形式的最小作用量原理只能针对机械能守恒且外力为保守力的情形,少了这些限制就无法得出这个最简形式。还有呀,上述数学味颇浓的推导过程导致后续的许多物理同僚质疑最小作用量原理只是一种有趣的数学变换,所以拉神的最小作用量原理并没有得到实际应用。
它的命运会如何发展?To be, or not to be, that is a question !
九、哈密顿原理
虽然拉格朗日的最小作用量原理没有激起太大的水花,但是拉格朗日方程可谓是威风凛凛,人称数学的一首诗!美如画也不过如此吧。后生才俊哈密顿受到这首诗的熏陶之后,宏伟目标也就随之浮现了: 要通过演绎方法从最少的公理去导出一个体系的完备表述 。显然,最小作用量原理被他看中了,而他要做的就是改进它。
这里我想简要提一提哈密顿的成果发布历程。被“数学的一首诗”熏陶过的哈密顿最早将目光投入到几何光学领域,想借用拉格朗日的思想方法去构建几何光学。天资聪颖的他做到了,并在这个过程里认识到了几何光学领域的最小作用量原理。而更能体现其水平的地方在于他将光学领域的成果类比到经典力学领域,从而重构了经典力学体系,也就有了本节的主题——哈密顿原理。
我啰嗦上面一段看似没营养的文字是希望读者明白:无论这个领域是实现了从0到1的飞跃,还是实现了从1到10的发展,都是大神们站在前人肩膀上进行接力赛的结果。即使再聪明的头脑,其迸发的思想火花都是有迹可循的。所以请读者牢记: 科学研究永远需要脚踏实地,鸡汤故事才需要夸张的天才素材 。希望读者在学习的过程中都能有正确的认识。
好啦,回到正事里来。要得到哈密顿原理,其实途径和拉格朗日非常相似,但是 哈密顿在处理变分的时候从一开始就一针见血的采用等时变分 ,这是他比拉格朗日做得好的地方。稍后大家就会看到哈密顿原理的表述,里面涉及的概念要清晰严谨得多!
至于推导出结果就非常简单了,因为可以把上一节中的主要推导过程直接复制过来。而且咱们在上一节里已经被拉格朗日鞭策过了,怎么说也会获得一些公式免疫吧。
有请1.0版本的动力学普遍方程入场:
这个版本的方程里没有涉及机械能守恒的假设,所以哈密顿可以放心的对其进行等时变分的处理。即 对于所有可能的路径,不仅起止位置相同,咱还要求对应的起止时间也相同 。如此一来,每条可能的路径对应的机械能就会不一样了。如果其中一条路径有机械能守恒的特点,那么其他路径就没有这个特点了。不过没关系,反正1.0版本的方程里就没这个限制。
接下来只需对这个方程两边积分:
这个操作咱们已经见怪不怪了。显然等式左侧的积分结果为:
因为所有可能路径的起止位置一样,所以路径函数在这两处的变分为零,即:
只需这么简单的一步,咱们就得到了哈密顿原理,即:
不是,这是哪跟哪啊?看起来还不如拉格朗日给出的最小作用量原理呢。哎呀,不着急嘛,这个等式是哈密顿原理的一般形式,如果你想得到简化版的表达式,来嘛。
你可还认识
哦豁,咱们在前面不是把拉格朗日函数定义成
咋样,这简洁程度是你想要的不?清晰明了的推导过程换来如此简洁的结果,你还能不爱么?其实在第七节结尾处咱们就发现了端倪:只要把目标泛函
里的
哈密顿给
于是乎,哈密顿就甩出了原理: 保守的、完整的力学体系在相同时间内,由某一初位置转移到另一已知位置的一切可能运动中,真实运动的主函数具有稳定值 ,也就是有:
嘘,我知道你会疑惑啥。先说保守的事,只有在保守的条件下,作用量才能写成这个最简形式。不过前文已经谈过了保守与非保守的问题,按照目前的观点,所有的相互作用都可归纳为四种基本相互作用,而这四种基本作用全是保守的。从这个角度来看,咱们可以不用去纠结非保守的情况。倘若你非要盯着非保守的情形,那么把哈密顿原理的一般形式拿去用喽。
再来说稳定值。稍微有点高中数学底子就能明白, 对于一个函数来说,如果它的导数在某处的值为零,并不意味着这个函数在此处取到了极小值!因为还有可能取到的是极大值,甚至并非是极值。但是这些情况下统称为函数取到了稳定值 。类似的,当泛函的变分等于零时,也只能说泛函取稳定值。只是在很多物理现象里,作用量确实取的是最小值,再加上历史上一直都这么称呼的,所以最小作用量的叫法也就没有更正过来。
扫清疑惑后是不是就发现这个主函数香得不要不要呢?从它可以推导出拉格朗日方程或者动力学普遍方程,也就意味着经典力学范畴里的结论都可以由它推导出来了。这种由最少的公理推导出更多结论的理论体系正是哈密顿所追求的!他小子做到了!
更出乎他意料之外的是,哈密顿原理在经典力学范畴之外也能如鱼得水,这就甩牛顿运动定律好几条街了。高中生都很熟悉的牛顿力学有它的局限性,在电磁领域、高速领域、微观领域都不适用,但是哈密顿原理直到如今仍然担当着统一性原理的角色。从此,哈密顿原理实至名归地走上神坛,被封为“第一性原理”!
第一原理(英语:First principle),或称作第一性原理,哲学与逻辑名词,是一个最基本的命题或假设,不能被省略或删除,也不能被违反。第一原理相当于是在数学中的公理。最早由亚里士多德提出 #viaWikipedia
在物理学中,第一性原理,或称从头算 (ab initio),指从基本的物理学定律出发,不外加假设与经验拟合的推导与计算。例如利用薛定谔方程在一些近似方法下解电子结构(英语:Electronic_structure),但不从实验数据得到拟合参数的从头计算法
英文维基: 在数学和形式逻辑中,第一性原理被称为公理或假设。在物理学和其他科学中,如果理论工作直接从既定科学的水平开始,并且不做出经验模型和参数拟合等假设,则称为从第一性原理或从头开始。“第一性原理思维”包括将事物分解为给定领域中的基本公理,然后通过询问哪些公理与手头的问题相关来推理,然后根据所选公理交叉引用结论并确保结论不违反任何基本定律。物理学家将反直觉的概念纳入重复推理。
这里不得不进行一下咬文嚼字,物理学里面有定律、定理和原理的说法。 定律是大量实验现象的总结;定理是基于定律给推导出来的;原理是从大量定律中抽象出来的能够用来推导定律的框架 。比如牛顿的三大定律、机械能(动量)守恒定律、电磁感应定律等;比如动能定理、动量定理等。比如伽利略的相对性原理、最小作用量原理。看着这些熟悉的名称,定律、定理和原理之间的差异是不是就一下子体现出来了?
作用量说到这里差不多可以告一段落了。毕竟它里面的玄机需要在更广的范围里去体现,这个就得看我本人的悟性了。我争取把这个系列的文章写下去,因为我也很想体会这其中如痴如醉的美。
对喽,哈密顿不仅改造了作用量,还改造了拉格朗日方程,得出了一组更简洁、更有特点的方程。既然来都来了,那就和我一起去瞧瞧吧。
十、哈密顿方程
拉格朗日方程的诞生给解决复杂力学问题带来了福音,不过也增添了一些挑战——毕竟拉格朗日方程是一个二阶微分方程,要求解未知数得积分两次才行。要知道积分运算可比微分运算麻烦得多,况且你还要积分两次,想想都觉得头大。所以哈密顿对方程的改造就是从降阶开始的。
咱们再把拉格朗日方程组揪出来瞧瞧:
方程数量有
接下来咱们所说的降阶就是从这一项开始改造的。想想中学里解一元二次方程时,老师是不是教过我们一种办法叫做换元法?你有二次项没关系,咱把你替换掉!这样就能把方程化成一次方程。
类似的,哈密顿也是采用换元的做法。把广义动量拿出来,即
你看,从形式上方程不就降阶为一阶微分方程了么?
想法挺好,只是中间还有很多工作要做。难道你只管替换第一项,就不管第二项了?这就好比甩给你一个一元二次方程
回到拉格朗日方程里来,原本方程组只有
你想想,引进的
假如
按照这个思路,
很明显,如果
此话一出,你看到
利用前面引进的换元
你瞧,在这个式子里出现了
另外,由于未知数只有
好吧,我承认构造的活有点像几何里作辅助线一样,存在一定的思维创造性和跳跃性,但思路既已到此,咱们也别无选择。这里我就直接给出
由于
睁大眼睛看,接下来你将体验到函数
把
另外,由于
喏,照妖镜在此,妖怪还不快快显出原形?!所以对应项一一相等,即:
你瞧这第一个等式,咱一下就把
别急,我知道你想说啥,这不还有添头:
可不嘛!偷偷告诉你,更大的惊喜在后面哟!如果咱们面对的是一个保守体系,那么就存在一种势能
由于势能只是广义坐标的函数,则有:
这个做法咱们在前面推导拉格朗日方程的时候就用过了。
好啦,最后偷个懒,令
这里有
啧啧啧,整形过后的拉格朗日方程不仅变成了一阶方程,还贼对称! 如果说拉格朗日方程被称为一首诗,这个方程组以神话自居绝对是当之无愧!这便是大名鼎鼎的哈密顿方程 。
方程里除了未知数,这个
请问你有没有觉得最后两项很眼熟啊?拉格朗日函数为
对了,咱们在第八节中推演拉格朗日的最小作用量时就发现
这是啥?这不就是系统的机械能(暂只考虑力学系统)吗?我的天呐,对于稳定体系来说,它的机械能对广义坐标的偏导、对广义动量的偏导所得出的方程就能描述物体的运动规律!
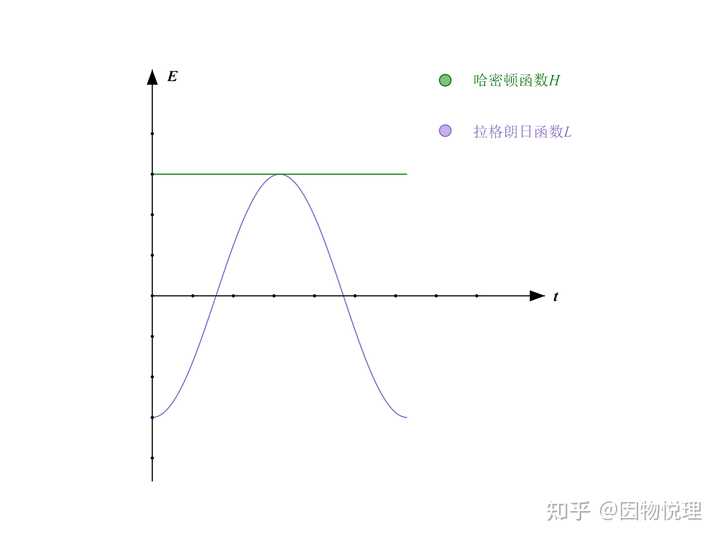
如果系统的机械能守恒,那么哈密顿函数与拉格朗日函数的差别就体现在各自对时间变化的规律上
哈密顿方程说到这里,你有没有发现它其实就是另选了一套坐标体系: 以广义动量
十一、一统江湖1
哈密顿原理之所以被后来人推上第一性原理的宝座,这和物理学的根本任务是分不开的: 对于一个系统,咱们得找出它的真实运动状态 !可是不同的系统就会有不同的具体描述方式,你看力学系统就是关心它的位置如何变化,经典力学领域用牛顿运动定律来描述;电磁领域关心的就是电场和磁场如何变化,得用麦克斯韦方程组来搞定;而热力学系统又得另起炉灶。
请问你想不想偷个懒——绕开这些具体的、不同形式的方程来回答“什么是真实运动状态”?如果真能偷懒,岂不是一本万利的买卖?有这等好事,傻子才不干呢!不过思来想去,要实现偷懒,咱们就只有一种办法——是骡子是马,拉出来溜溜! 将所有可能的运动状态都拿出来海选,从而在里面找出真实的运动状态 。这么一来,不管是啥类型的系统,这种“笨”办法不就可以通吃了么?
你瞧,这个“笨”办法和哈密顿原理的思想不正是王八看绿豆——对上眼儿了么?这种路线正确的原理,你不把它放第一位放哪?再者,原理本身是无法直接给予证明的,得通过它推出的一些列正确的、自洽的结论来加以佐证。而哈密顿原理都经受住了这些严格地考验。 所以咱们海选的依据就是作用量,即一个物理系统实际发生的真实运动状态是所对应的作用量具有最小值(稳定值)的那个状态 。
好啦,现在开局一张图:
经典力学领域的规律被牛顿支配得明明白白,其核心就是牛顿三大定律。第一定律是说物体总保持静止或匀速直线运动状态,除非有力作用在物体上使其改变运动状态;第二定律就是大名鼎鼎的
而经典力学领域要解决的问题就是如何描述物体的机械运动,也就是搞清楚物体的位置变化有啥规律 。咱们一开始接触物理的时候就知道,要判断物体的位置有没有变化需要找一个参照物,也就是参考系。虽然参考系可以任意的选取,但是牛爷的理论只能在惯性系中成立(不然就得加上虚无的惯性力了,咱们在第六节提到过)。 就是说被选为参照物的对象必须是静止或者是匀速直线运动状态或者是这个对象不受任何的外力,以此为基准来描述物体的运动才能用上牛顿三大定律 。
这样的参考系有没有呢?反正牛顿在其著作里就直接假定了宇宙深处有这么一个绝对的惯性参考系,它远离任何星体,所以它不受任何力的作用,自然就是牛顿心目中的白月光啦。不过有个问题咧,如果咱们只是想研究眼前物体的运动规律,是不是也得选远在天涯的绝对惯性系呢?那不得麻烦死啊?!
看到这个问题,教父级大神伽利略云淡风轻地笑而不语,默默地扔出了两件宝贝: 伽利略变换和伽利略相对性原理 。先说伽利略变换,假设你相对地面的行走速度是
将其上升到理论的高度,假设现有两个不同的参考系
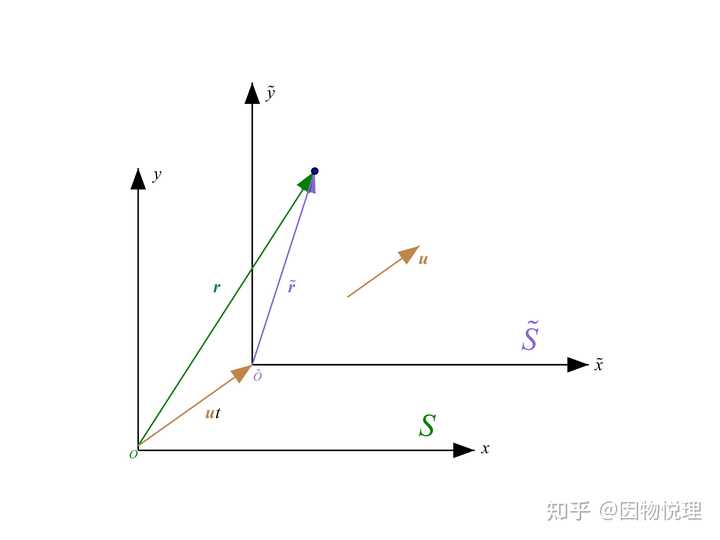
并且我们认定在两个参考系里,时间
基于此才有了例子里速度叠加的运算,即把上式两边对时间求导,则有:
如果这两个参考系都是惯性系,把位矢关系式的两边对时间求二阶导数,则有:
等等,咱们不是要从哈密顿原理去推演经典力学的体系么?怎么无缘无故地说起伽利略了呢?是这么回事,你要知道咱们现在也就一个哈密顿原理,至于那个
回到左膀里来,既然在不同惯性系中所有力学规律是等价的,而力学体系的全部性质都集中在拉格朗日函数身上,所以 相对于不同惯性参考系来说,力学体系的拉格朗日函数所满足的方程肯定是相同的 。敲黑板啦,并不是说力学体系相对不同参考系的拉格朗日函数一样。因为 由一个力学体系不能完全决定对应的拉格朗日函数,其后还可以添加一个“任意常数” ,这和求不定积分很类似。
这里的“任意常数”并不是我们理解的一个不变的数字,而是根据哈密顿原理推出的一个只与广义坐标和时间有关的任意函数对时间的全导数,即有:
这里的函数
为啥会有这个特点呢?因为根据哈密顿原理,当对作用量取等时变分时,有:
由于哈密顿原理中有端点的限制条件,则有:
显然就有
再来说一下右臂,哪个搞物理的人不希望看到物理理论的普适性? 这种能放之四海而皆准的特性除了能反映出物理规律有很宽的管辖范围外,还意味着物理规律满足对称的特点 。啥?对称?这不是个几何特征的词么?
是的,单纯说对称确实指的是几何特征,比如你把一个正三角形实施绕中线对折、绕中心旋转等操作,你会发现操作前后得到的图形是一样的。 将对称性引申到物理规律中去,意味着把物理规律也实施某些操作后依然有相同的结果 。比如你换个时间、换个地点去做同样的实验,只要实验条件完全相同,你得到的实验结果就是一样的,即物理规律并没有随时间或者地点的变化而变化。这两个基本的对称性被称为 时间平移的不变性 和 空间平移的不变性 ,时空还有其他的一些对称性这里就暂且不列了。
不过咱要实话告诉你,时空对称性其实是人们的一种假设,是对自然界是简洁的执念。现有的物理理论可都是建立在这个假设之上的,因为咱们坚信物理定律的普适性。倘若今后发现在宇宙的长河里,某段时间或某个区域里存在着不同的物理规则,那么现有的物理大厦估计就得重建了,毕竟地基歪了嘛。这事又不是没有发生过,百年前的两朵乌云不就干引发过一场轰轰烈烈的拆迁运动么?
咳咳,哥本哈根学派有一句名言: 先有自然才有人类,但是先有人类才有自然科学。我们人类需要理解大自然才创造了这些叫自然科学的产物,但是大自然从来不需要理解人类创造的自然科学 。
有了这些铺垫,我们就要开始大展身手了哈。本着由易到难的打怪顺序,咱们首先要解决的问题就是推出不受任何作用影响的自由质点的运动规律。
自由质点相对惯性系运动时,时间与空间具有的平移不变性的特点怎样在拉格朗日函数中体系出来呢?这意味着拉格朗日函数里不显含时间和物体的坐标,如此一来,拉格朗日函数就只能是速度的函数。另外,空间的均匀性还意味着拉格朗日函数与速度的方向也没关系,即拉格朗日函数只能是速度大小的函数。由于速度
函数的变量给定下来了,但是咱们还不清楚函数的表达式,所以还要继续猜。考虑到伽利略的相对性原理,针对同一个力学体系在两个不同的惯性参考系中运动,假若两个参考系之间的相对速度无穷小,极限情形下,这个力学体系的运动轨迹肯定是一样的。如此一来,变换前后的拉格朗日函数虽然有所不同,但是只能相差一个仅与坐标(对于自由质点,用不着广义坐标)和时间有关的任意函数对时间的全导数。
假设物体相对参考系
接下来咱们要用到一个数学公式,这是整篇文章里唯一一次没有任何铺垫就甩出了公式。我尽力了,毕竟数学工具到用时方恨少呀。 这个公式就是大名鼎鼎的泰勒展开式,也就是把一个连续可导的函数用多项式去无限逼近 。其实高中物理里就用到过这个结论,比如单摆要求摆角很小,只有这样才有
泰勒公式:
为函数
数学工具用起来吧。对于
由于
对比泰勒公式,我们将
于是用泰勒公式展开以后的结果就是:
前面我们已经猜到了拉格朗日函数
咱们把等式右边按照求导的链式法则展开,即有:
也就是有:
看好了!考虑到
由于
常数
好家伙,咱们只根据两个原理就猜出了自由质点的拉格朗日函数,它居然是咱们熟知的质点动能 。熟悉归熟悉,这结果可靠不?这还得用更多的事实来验证它。
上面咱们是借助两个惯性参考系之间只有无穷小速度的极限情形去猜出拉格朗日函数,但是实际情况里,两个惯性参考系之间更多的是存在有限的速度(暂不考虑高速的情形,目前超纲了哈)。如此情形下,刚才猜出来的结论能经受考验不?
假设两个惯性参考系之间的速度为
根据伽利略相对性原理,在不同惯性参考系中的所有力学规律都一样,那么对于同一个自由质点来说,这两个拉格朗日函数也就只相差一个只与坐标和时间有关的任意函数对时间的全导数。
来吧,变形看看:
由于
你瞧,括号里不正好是一个只与
还有利好消息!自由质点在惯性系中怎么运动呀?想必大伙都知道答案——保持静止或匀速直线运动状态!这是大名鼎鼎的牛顿第一定律呀。那么拉格朗日函数及其方程能给出这个结论?
由哈密顿原理推出的拉格朗日方程,即:
咱们现在已经猜出了自由质点的拉格朗日函数为
由于
如果咱们只研究自由质点的运动肯定不够呀,怎么着也得来点相互作用吧?要不然要牛顿第二、第三定律有何用呢?
既然要来点相互作用,就得增加更多的质点,这样彼此之间才会产生相互作用嘛。一步步来, 先假设有
如果把这个大体系弄小,让里面的
奇怪哎,这个与质点间相互作用有关的函数
这...这说明了啥?你想呀,现在的这一坨存在相互作用的质点可不再是自由身啦,它们间的相互作用会直接影响到彼此的运动。 如果彼此间的影响随着选用的惯性参考系不同而有先后之分,那意味着该质点系在不同惯性参考系里的运动规律就不一样了,这可正好与伽利略的相对性原理相矛盾呀 。哈哈哈,谁还不是读着伽利略长大的呢?他那一套反证法咱用得麻溜着呢。
如此一来,这个质点系的拉格朗日函数就只是速度
就这?你在逗我吗?
别急,好戏才刚刚开始。质点系的拉格朗日函数不是满足拉格朗日方程:
眼瞅着越来越复杂了吧?其实不然,等式右边不正好是两个函数乘积的求导展开式么?先不要往后看结果,看看自己能不能写出答案。没错,等式变成了:
再移个项,局势就明朗了,即:
一个函数的导数为零,说明这个函数是个常数。所以
那么就有:
也就是说
你看这个结果,第一项是质点系的动能, 根据量纲可以推测第二项肯定也是能量 !不然的话,这两项怎么进行相减呢?
等等,咱们好像只听过能量相加时是常量的情形,也就是能量守恒,这里出现的是减号是不是有点小讨厌呢?
没关系,咱们既然已经确定了函数
简记为:
由于咱们现在考虑的对象只是宏观低速领域的力学体系,什么电啊、磁啊、分子啊、原子核之类的通通不予考虑。而且这个
我的天呐,本来只想着猜出自由质点系的拉格朗日函数,一不留神把机械能(动能加势能)守恒给推导出来了。意不意外、惊不惊喜?哦,想起来了,咱们的初心是要推出牛顿第二定律和第三定律,要不你先平复一下激动的心情,我们去见证更多的精彩吧。
现在已经得出了 自由质点系的拉格朗日函数 :
即系统动能和系统势能的差。由于牛顿第二定律是针对单个质点的规律,所以咱们需要把这个拉格朗日函数推广到受外界相互作用影响的单个质点的身上。
请不要重复造轮子,咱们完全可以把刚才的那个自由质点系一分为二嘛:待研究的单个质点
这里的前两项分别是
咱们现在的目的是得到处于外部场中的单个质点的拉格朗日函数,所以
发现没,在外场中运动的单个质点,它的拉格朗日函数依旧为通常的形式,差别只在于势能可能显含时间。所以将这个质点的拉格朗日函数记为:
将其带入到拉格朗日方程可得:
等式左边是将质点的动量对时间求导,由于物体的质量是常数(低速领域),所以结果为:
再把
什么,力能这么定义?为啥不可呢? 你要知道,按照牛顿力学的发展历程,是先定义了力,后来才有势能的概念。现在只不过是反过来了而已,为啥不行 ?
厉害呀!把一个小小的拉格朗日函数捣鼓一下,牛顿的两个定律就现原形了。咱们一鼓作气,看看能不能推导出牛顿第三定律。
在牛顿力学的发展历程里,牛顿第三定律来源于对碰撞现象的规律总结,这在我之前的文章里有所提及(戳我)。惠更斯在研究碰撞现象时明确指出了动量守恒的特点,牛顿老爷子由此悟出了 物体间的相互作用力满足等大、反向、作用在同一直线上的特点 ,这就是大伙熟悉的牛顿第三定律啦。所以,接下来就是要看看哈密顿原理能否推出系统动量守恒这个特征。
说到守恒,上面在推导牛顿第二定律时,无意中用到了时间均匀性的特点。空间不也有均匀性么?那么通过这个特点是不是也能发现啥呢?
假如空间具有均匀性,那么一个封闭系统在空间里整体平移之后,其性质保持不变。这就好比有两套完全一样的房子,所有因素完全一致,你住哪套不是住呢?对吧?既然如此,倘若咱们把这个系统里的所有质点都平移相同的位移
咱们早就知道了封闭系统的拉格朗日函数只与系统里每个质点的速度以及每个质点的位矢有关,所以根据链式法则有:
由于质点只是做了整体平移,其各自的速度并没有发生变化,所以
各项准备工作就绪,咱们看看得到了啥:
一旦把这个结果带入到拉格朗日方程组
封闭体系的拉格朗日函数
这不就意味着系统的动量
至于想得到心心念的牛顿第三定律也非常容易。根据封闭体系的拉格朗日函数
由于:
这不正是作用力与反作用力的特点——等大、反向、作用在同一条直线上么 ?
好啦,现在咱们要收网捋一下了。从哈密顿原理出发,只需借助伽利略相对性原理、并假设时空具有对称性,那么经典力学的所有规律全给弄出来了。哈密顿曾经的信仰——从最少的假设或者原理出发去构建整个物理体系,现在就在经典力学领域得到了实现!
嘿,请收下我的膝盖,让我有资格膜拜吧!
十二、结语
正如前言里面所说,我写这篇长文的目的就是想体验物理规律的普适性所带来的震撼。写到此,我终于可以松一口气,自我感觉已经做到了剥丝抽茧。相信能一口气看完全文的读者或多或少也能有所体会。
在写文章的过程中,我最大的感触就是只有能把自己给讲明白了,才能写出逻辑清晰、严谨自洽的文字。可能是自己当老师的缘故吧,我早已习惯了把学习过的东西以非常通俗的方式表达出来,所以有太多次面对一个概念、一个公式、甚至是一个符号时,我都会费尽心思去查找资料,只为了能让自己彻底明白。如此,我才能写出让读者易读能懂的文字。
最后,我发现学习也好,写文章也罢,这是能上瘾的。当我一次次输出有着自我理解的文章时,它们能反过来极大提升我的学习效率。而且这样的文章还很荣幸的受到一些读者的喜爱,幸福指数蹭蹭往上涨了不少哟。
咋样,你也想拥有这样的学习状态吗?那就请不要放过任何一个你面对的疑点,想办法干掉它,量变过渡到质变就会在你身上出现!到时你就尽情享受学习带给你的红利吧。