交换群、域和有序域

我们首先看几个例子：

例子一、 设 是整数构成的集合，我们用 表示通常意义上的加法和乘法。我们知道，它满足下面的性质：

交换律： ,
结合律：
有单位元：
可逆性：对于任意 ,

例子二 、 设 是一个正整数， ，我们定义的一个「加法」 :
我们定义 为 除以 后的余数。于是， .

交换律： ,
结合律：
有单位元：
可逆性：对于任意 ,

例子三、 设 是非零的有理数构成的集合，对于一般的乘法，我们有

交换律： ,
结合律：
有单位元：
可逆性：对于任意 我们存在 使得

在上面三个例子中，我们有一个集合 ，和一个「运算」 , 这个运算就是一个从 到 的映射（ ）。这个映射具有对称性，满足结合律。存在一个单位元 ，使得
。对于任意 , 存在 使得 .

综合起来，我们有：

定义 ：设 是一个集合， 是一个二元运算。假设下面四个条件成立，我们称 是一个 交换群。

交换律： ,
结合律：
有单位元：存在一个元素 使得 ，我们称之为 单位元 。
可逆性：对于任意 , 我们存在 使得 ，这个元素叫 逆元 。

阿贝尔群（Abelian group）也称为交换群（commutative group）或可交换群，它是满足其元素的运算不依赖于它们的次序（交换律公理）的群。阿贝尔群推广了整数集合的加法运算。阿贝尔群以挪威数学家尼尔斯·阿贝尔命名。阿贝尔群的概念是抽象代数的基本概念之一。其基本研究对象是模和向量空间。阿贝尔群的理论比其他非阿贝尔群简单。有限阿贝尔群已经被较为彻底地研究了。无限阿贝尔群理论则是目前正在研究的领域。

显然，上面三个例子都是交换群。交换群中的单位元是唯一的，设 是两个单位元，根据两者都是单位元，我们可得 . 根据交换律，我们有 。所以它们是一样的。

注意，我们在说群的时候是把「集合」 和「运算」 放在一起讲的，你绝对不能脱离运算谈群，你得指定那个运算（除非是显然的）。

例子四、 我们上面的例子中元素都是「数」构成的，但是 群 可以由任意元素构成，重点是你得指定运算，那些运算符合「条件」即可。设集合 正负

我们发现它有两个元素构成，一个叫「正」，一个叫「负」，我们 定义 一个二元运算 如下

首先有群的概念, 之后再定义环与域
环与域：在一个集合上定义两种运算“加法”和“乘法”，如果这个集合在这个“加法”下成群，而在这个“乘法”下只满足“封闭性”与“结合律”，则称这个集合与这两种运算构成一个“环”；如果这个集合去除“加法”群下的单位元后形成的新集合在“乘法”下成群，则称这个集合与这两种运算构成一个“域”。显然，“域”是一种特殊的“环”（以上不是环与域的严格定义）。

（这就是我们的定义，别问为什么）

我们可以发现这个运算满足交换率，而且「正」是 中的单位元（其他元素计算和它计算后不变）。「正」的逆元素是「正」，「负」的逆元素也是「负」。于是， 构成一个交换群。这个「群」有什么启示。

1. 群中的元素不一定是一般的数，可以是很一般的元素。
2. 群上「运算」不一定需要是传统的数的四则运算，而可以是相当「任意」的东西 。

那么这个群没啥意义吗？不是的，它其实其实正负数相乘后的结果。正正得正，负负得正。好，我们现在考虑群 ，你可以发现在这个群中 .

是不是和上面的 很像？

如果我们 构造映射 使得 正 ， 负 。不难发现

也就是说 和 这两个群是同样的结构，它们本质上一回事。 也就是说，我们可以 把正看成0，负是1， 是 。也就是说，要研究 只要研究 就好了。

现在，我们定义这个文章的主角：域。它的定义方式有很多种，可以通过「交换环」或者「除环」的方式定义。这里，我们通过一个较为简单的方式定义。

定义(Artin)： 设集合 上有两个二元运算，它们「叫做」 加法 和乘法 。如果下面三个条件成立，（） 叫做域。

1. 相对于二元运算 是一个交换群，我们称呼群 中的单位元叫零元素，写作0
2. 对于乘法是可交换的，并且 , (也就是 去掉零元素)，相对于二元运算 构成一个交换群，我们称呼交换群 中的单位元叫一元素，写作1
3. 两个二元运算满足分配律，也就是对于任意 ,

!!! Note

所以这就是为什么不需要再定义更多的 operator? 因为有两个 operator 后需要考虑分配律, "分配" 即是描述两个 operator 之间的关系, 于是引入第三个 operator 也不会带来新的变化了, 使用多次分配律就能搞定
复制

首先，一个域中的加法和乘法不是「真正」的加法和乘法，只是一种方便区分的 叫法 罢了。

第二，在域上，我们可以自然的 定义减法和除法 ，对于任意 , 我们可以用 表示 在群 中的逆元，那么我们定义减法 。类似的，对于任意 , 我们用 表示 群 中的逆元，我们定义除法 .

第三，对于任意 , 。根据交换性，我们只需要证明 即可。实际上，根据分配律和 ，我们发现 ，两边减去 即可发现 .

第四（ 上的乘法结合律）：根据定义，我们知道结合律在 上的成立的，那么在 它成立吗？我们只需要证明当 中某个为0的时候， 成立。根据上面的结果三，上面等式两端都是0。

第五（消去律成立）：如果 , 那么 . 两边呈上 , 于是我们有 . 利用第四点中得到结合律，我们发现

数域的平凡例子包括

1. 有理数 和一般的加法和乘法构成的域
2. 实数 和一般的加法和乘法构成的域
3. 复数 和一般复数上的加法和乘法构成的域

一个比较有趣的例子 ，我们在上面定义「取余数」的加法和乘法，
也就是说 和 分别是 以及 后除 的余数。
我们上面已经证明过关于加法 ， 是一个交换群。
另一方面，按照定义，我们知道交换律 成立，我们得证明
确实能构成一个交换群， 首先 是其中的单位元。结合律也是显然成立的，难点在于对于任意 , 是否存在一个元素 使得 除以 的余数为1. 这里我们需要利用一下费尔马小定理：

https://zh.wikipedia.org/wiki/%E8%B4%B9%E9%A9%AC%E5%B0%8F%E5%AE%9A%E7%90%86

利用它我们知道，对于 除以 的余数为1。所以，我们只需要找 在 中的余数即可，确切的说，。因此，我们有 。因为 除以 的余数为1，所以 除以 的余数为1. 所以 是一个域。

这段是为了找到 y, 最后结论是 除 p 的余数就是 y, 这个 y 满足 xy 除 p 余 1

还有一个例子是

,
上面的运算就是一般的加法和乘法。

就好像群论不限定于「数」一样，一般的「集合」上也能定义域。
设

, 我们定义如下加法和乘法，也就是两个字母的运算结果
就是对应字母横纵的交叉点的字母。

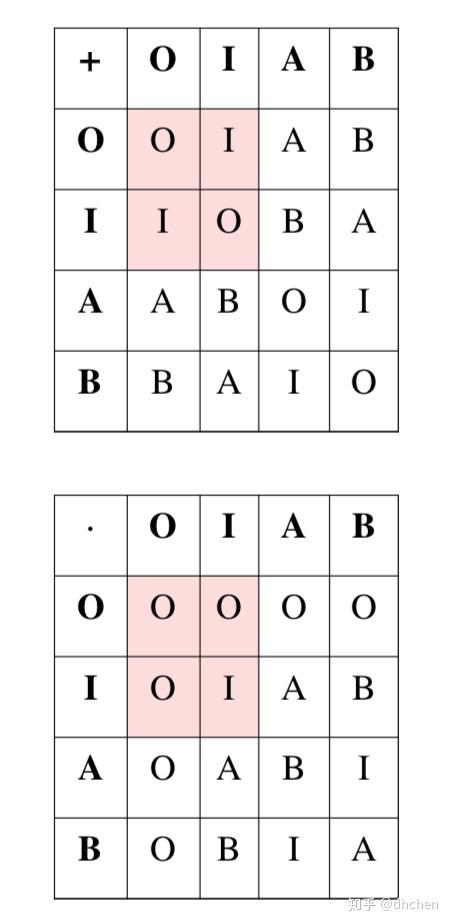
作为习题，大家可以试试看能不能看出来 它 构成一个域 。

我们知道实数和有理数不单单可以四则运算，也可以比较「大小」。在数学上所谓的比大小，本质上就是一个「序结构」。

一个集合 上的全序是一个（二元）关系 , 它满足下面两个条件

1. 任意 , 下面三个关系 必然有一个成立。
2. 如果 , 成立，那么 成立。

我们称呼 是 全序集 。我们举一个例子，, 我们规定 , 那么 构成一个全序集。反过来，我们规定 , 那么 也构成一个全序集。

定义：有序域 是具有全序结构的域，而且我们要求它满足下面两个（相容性）条件

1. 如果 , 那么 必然成立.
2. 如果 , 那么 必然成立.

显然 和 都构成一个有序域。
一个有趣的结果是带序数域必须有 无限个元素 ，否则我们设 是 的最大元素。
根据 最大，我们有 , 因此 . 这是矛盾，因为 比最大元素 更大。所以，我们上面构造的有限数域 不可能变成一个有序域。
单纯的具有序结构的数域自然未必是「带序数域」了，比如 ，我们自然可以定义 , 但是这个全序结构不满足上面两个相容性条件。

带序数域是及其稀少的，比如复数就 不可能是一个有序域 。
我们用反证法来证明这点，假设存在某个全序结构 使得 变成一个有序域。

第一步，我们证明 . 否则的话，我们设 , 于是我们有 . 但是根据 ，我们两边加一可得 . 矛盾。
第二步，我们证明 . 否则的话，我们有 , 然后我们可得 . 这和第一步矛盾，于是可知 。
第三步，我们证明 . 否则的话，我们有 , 然后我们可得 . 这和第一步矛盾，于是可知 。
第四步，我们发现第二步和第三步是矛盾的，因为如果第三步成立，那么通过 两边加上 , 那么 , 和第三步矛盾。

综合以上所知，复数就 不可能是一个有序域 。

群、域和有序域是传统的乘法、加法和大小关系的推广，这种定义允许我们在 一般的元素集合 上定义类似于传统乘法/加法的运算。我们发现即使只需要一些抽象的定义，也能得到丰富的结果，这种抽象能够让我们去忘记肤浅的表象， 只是通过抽象化得到了更清晰的结果。

在实际物理学的研究中，很多物理上的行为也被对应为某种群/数域结构。在历史上，数域一个经典运用就是处理一般5次方程是否存在(基于常数的)通解的问题，还有一个运用就是 处理实数问题，这也是我会在Live中仔细论述的内容。

回到实际构造「数」的问题，数学追求一种简洁美，也就是用尽量少的假设和公理推出尽量多的结论。对于我们常见的数，其实根本公理是皮亚诺公理（和集合论），它允许我们定义「自然数」，然后我们利用自然数构造出恰当的交换群「整数」，本身带有序结构。在 整数 的基础上我们再利用它们构造出一个带序域 有理数，构造实数核心在于找到恰当的「元素」和「运算」，基于「有理数」从而构造出一个「恰当」的有序域。而这个也就是live的核心了。

编辑于 2018-07-22

数学

高等数学

代数

赞同 638

原网址: 访问

创建时间: 2021-03-24 13:09:09

目录: default

标签: zhuanlan.zhihu.com