一样的数据不一样的结论—— 《为什么》笔记上篇

去年，朋友推荐了《The Book of Why : The New Science of Cause and Effect》¹，中文译本为《为什么 : 关于因果关系的新科学》。其第一作者是Judea Pearl，2011年计算机图灵奖的获得者，作者在因果科学上面有很多研究。这本书是最新的科普读物，它在在国外，国内的读书网站评分都很高。朋友的推荐，加上这本书本身评分很高，自己又对这个领域十分有兴趣，我半年前把这本书的英文原版买到手，作者将因果关系的前世今生娓娓道来，让我对整个世界的运作规律有更深刻的认识，自己想了很久的很多问题也有了答案。这篇文章想分享自己一些感受，希望对大家有所启发，也推荐大家有时间看看原文充分感受作者的思想，不习惯阅读英文的朋友也可以看中文译本。

数据+假设=因果 ，光从数据得不出因果，人们常说的用数据说话，往往是利用了一些假设，当然有一些假设是显而易见的，使得人们忽略了这些假设。我们先从下面的数据说起，最后会看到书中提到了另外一个 一样的数据不一样的结论 的案例。

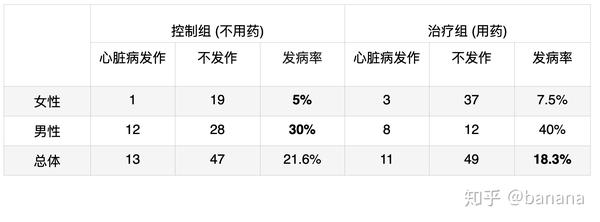
一种药物和心脏病发作的关系，人数统计结果

为了研究一种药物和心脏病发作的关系，有如上表的实验统计结果，左边是控制组，不用药，右边治疗组，用药。如果看分别对女性和男性的心脏病发作的统计数据，你会发现对男性，女性单独比较发病率，控制组发病率更低。但是从总体来看，治疗组发病率更低。那问题来了，这种药到底可不可以降低发病率？是性别已知的时候不能，性别未知的时候可以？这种情况称之为辛普森悖论，其它的知乎文章²也有提到。

当人们尝试探究两种变量（比如新生录取率与性别）是否具有相关性的时候，会分别对之进行分组研究。然而，在分组比较中都占优势的一方，在总评中有时反而是失势的一方。该现象于20世纪初就有人讨论，但一直到1951年，E.H.辛普森在他发表的论文中阐述此一现象后，该现象才算正式被描述解释。后来就以他的名字命名此悖论，即辛普森悖论。此悖论的最终原因和选择偏差、幸存者偏差、以及柏克森悖论一样，是源自对撞因子。

请看下面的例子：一所美国高校的两个学院，分别是法学院和商学院。新学期招生，人们怀疑这两个学院有性别歧视。现作如下统计

法学院

性别	录取	拒收	总数	录取比例
男生	8	45	53	15.1%
女生	51	101	152	33.6%
合计	59	146	205

商学院

性别	录取	拒收	总数	录取比例
男生	201	50	251	80.1%
女生	92	9	101	91.1%
合计	293	59	352

根据上面两个表格来看，女生在两个学院都被优先录取，即女生的录取比率较高。现在将两学院的数据汇总：

性别	录取	拒收	总数	录取比例
男生	209	95	304	68.8%
女生	143	110	253	56.5%
合计	352	205	557

在总评中，女生的录取比率反而比男生低。这个例子说明，简单的将分组数据相加汇总，是不能反映真实情况的。

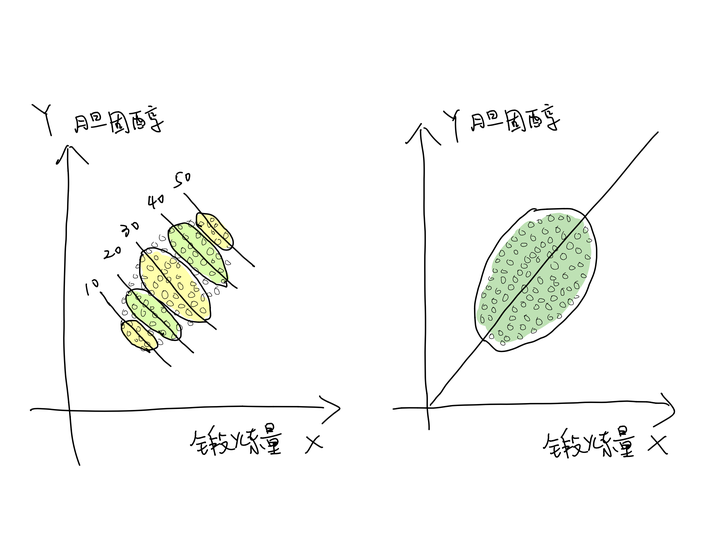
借助一幅向量图可以更好的了解情况

1

女生单独两个矢量斜率都比男生大，说明它们的比率都比较高。但最后男生总体向量斜率却大于女生

对撞因子（英语：Collider），有时又称为反向分叉（英语：inverted forks），在统计学和图模式中，是指同时被两个以上的变数影响的变数，而这些影响对撞因子的变数之间不见得有因果关系。因为在环路图上会显示为有两个以上箭头指入的节点，所以称为对撞因子。对撞因子不会直接造成影响它的变数之间出现相关，以路径分析或环路图的术语来说，对撞因子会“阻断”两个变数间的路径。然而，想要了解变数间的因果关系时，对撞因子非常重要，因为在设计实验、挑选样本或统计分析时，如果有意或无意间控制了对撞因子，会造成自变数（X）和应变数（Y）之间出现没有实际因果关系的伪关系，称为选择偏误或柏克森悖论，如果控制对撞因子后造成相反的相关性，称为辛普森悖论。用环路图的术语来说，控制对撞因子会“开启” X 和 Y 之间的路径，而造成偏误。

1

书中提到了另外一个数据表明这种数据的确存在。

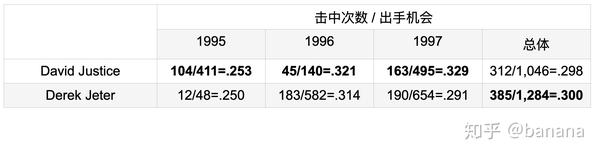
比较两名选手的命中率的数据

上表是一组比较两名选手的命中率的数据，如果分年份进行比较，我们会发现Derek Jeter每年的命中率都要更低，但是从三年总体来看他的命中率却更高。这是因为Derek Jeter在1996年命中率最高的时候有大量的出手机会，而另外一名选手相反，在命中率低的时候有大量的出手机会，这使得在统计三年平均值时Derek Jeter在命中率高的那一年权重更高，使得总体命中率更高。

心脏病药物的辛普森悖论当中：

1. 治疗组女性更多，这表明女性更愿意用药，性别会影响患者用药的意愿，影响患者所在的组。
2. 控制组和治疗组女性的发病率都要比男性更低，表明性别会影响发病率。

女性偏爱用药，同时女性的发病率低，我们收集到的总体的数据当中自然出现有用药导致发病率低的情况。因为性别的影响，我们不能直接从收集到的数据当中得出用药和发病率的关系。我们可以假设性别，是否用药和心脏病发作有如下的关系，为了消除性别的影响，我们分别对男性，女性统计发病率变化，然后通过现实世界当中男性和女性的比例对发病率进行1：1加权平均得到最终的结果，结论是这个药物会不能降低发病率。

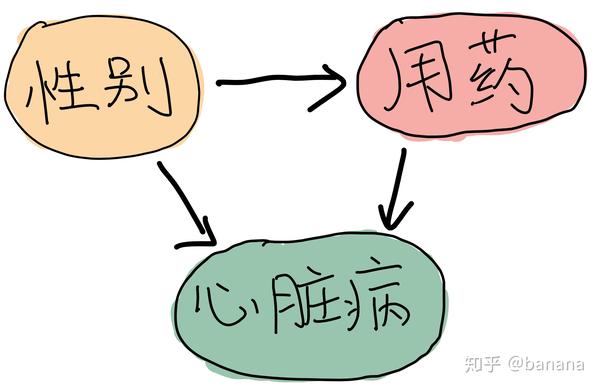
性别，是否用药和心脏病发作的假设

为了进一步解释这种情况，书中用可视化的方式展现了一个案例。

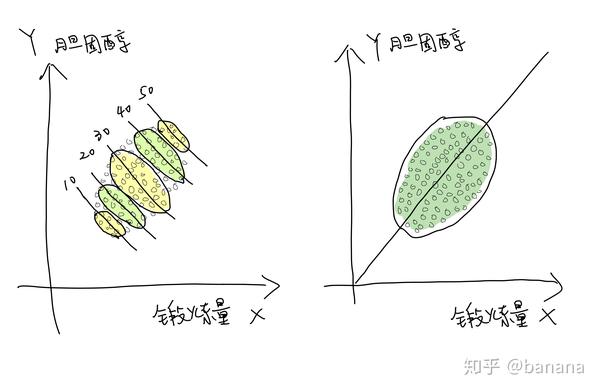
X轴为锻炼多少，Y轴为胆固醇含量，每个圆点代表一个人的锻炼情况和胆固醇含量

上图当中的左右两图，X轴为锻炼多少，Y轴为胆固醇含量，每个圆点代表一个人的锻炼情况和胆固醇含量。左图，每个年龄层的数据被分别圈起来了，单看某一个年龄层，锻炼得越多，胆固醇含量越低。但是从右图的整体来看，锻炼越多，胆固反而醇含量越高。这是因为我们收集到的数据当中，年龄越大的人越喜欢锻炼，而年龄越大其胆固醇越高，我们收集到的数据当中就存在锻炼越多胆固醇越高的现象。我们可以有如下的关于年龄，锻炼和胆固醇含量的假设，分别对不同年龄层比较，再进行加权就可以得出合理的结论。

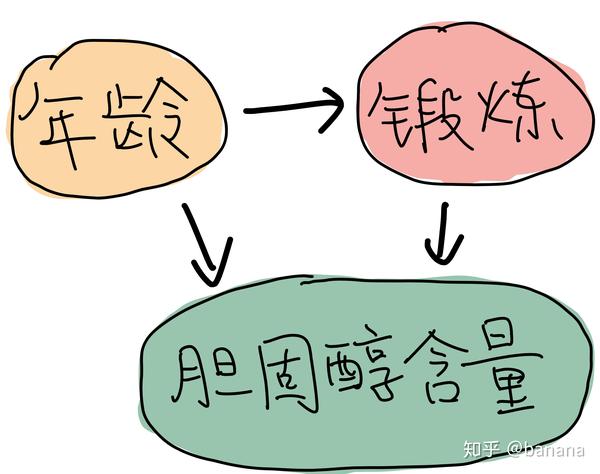
如下的关于年龄，锻炼和胆固醇含量的假设

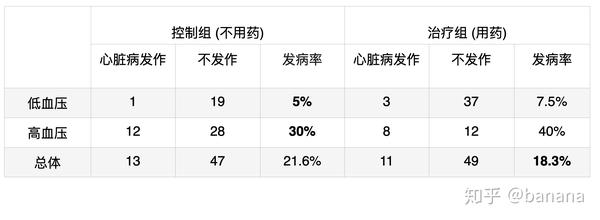
这个表格和最开始提到心脏病药物的案例有完全一样的数据，但是我们却可以得到出完全不一样的结论

上面的表格和最开始提到心脏病药物的案例有完全一样的数据，但是我们却可以得到出完全不一样的结论。在实验结束时，我们测量患者的血压，分别对高血压，低血压进行发病率的统计。我们得到了和之前一样的数据。但是这一次因为血压是用药的结果。我们可以假设药物，血压和心脏病的关系如下，药物成功地把高血压患者变成低血压，这使得最终治疗组的发病率降低，所以我们可以得出药物可以降低发病率的结论。

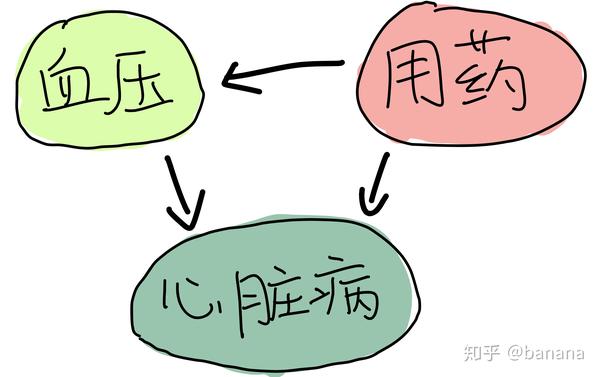
假设药物，血压和心脏病的关系

随着计算机硬件和互联网的发展，数据变得唾手可得，然而需要警惕的是只有数据无法得出正确的因果关系，甚至容易推导出完全错误的结论，我们不但要关注数据，还需要关注数据背后的产生过程，数据加上合理的假设才能可以得出正确的结论，很多工作之所以不能被高效处理数据的计算机代替，很大程度是因为机器没有办法提出这些人类觉得合理的假设。

这对机器学习工程师的直接启发有，如何消除推荐系统当中位置对点击的影响，工业界最新的工作包括有来自Youtube的 Recommending what video to watch next: A multitask ranking system，来自华为的 PAL: A position-bias aware learning framework for CTR Prediction in Live Recommender systems。

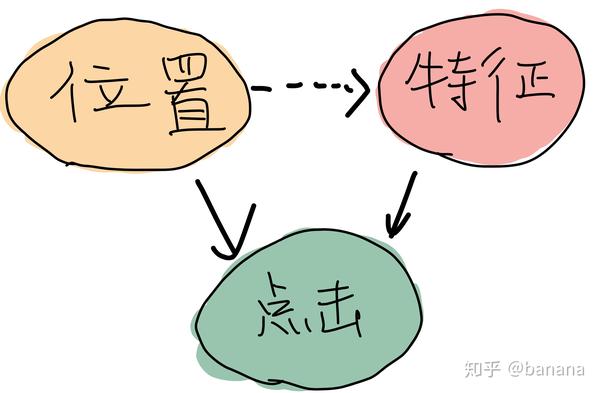
推荐系统当中位置对点击的影响

1. https://book.douban.com/subject/30139217/
2. https://zhuanlan.zhihu.com/p/95461240
3. Recommending what video to watch next: A multitask ranking system
4. PAL: A position-bias aware learning framework for CTR Prediction in Live Recommender systems