顺滑地进入群论 (Ep.3) ——李群与李代数

一个 上的代数 ，是一个 上的向量空间加上一个叫乘法的二元运算 ，将这个二元运算记为 ，它满足 其中 ， .

如果你对这个定义感到疑惑也没关系，它不影响你理解后续的内容.

李群描述的是连续的对称性，那么这个连续性要怎么理解呢？最直观的理解就是：假如我有一个描述连续作用的李群，那么这个李群中总有一个无限接近幺元 (即单位元，对应什么都不做的操作) 的元素. 我们可以把这个元素记为 其中 是幺元， 是一个无穷小的数. 后面这个操作 被称为 生成子 (generator) ，因为是它生成了这个无限小的变换 .

我们之前提到的 就是一个李群，因为它包含着无穷小的变换 ，即无穷小角度的旋转. 那么它的生成子是什么呢？现在我们想，如果要生成一个有限大角度的旋转，应该怎么做呢？显然的做法就是，用 个连续的无穷小旋转来逼近一个有限大的旋转，像这样： 要旋转一个有限大的 角度，我们可以尝试用 表示 中的 ，只要让 就可以了[3]. 这样一来，这个有限大的旋转就可以写为 可以看到， 在某种程度上定义了 这个操作，这就是为什么它被叫做生成子.

从上面可以看到，对李群 来说，它的群元素可以写成 的形式，其中 是一个实数. 那么为了构成一个代数，我们还需要知道两个李群的元素要如何结合： 李群元素之间的运算由 Baker-Campbell-Hausdorff公式 给出： 其中 被称为 李括号 (Lie bracket) . 可以看到，李群元素之间的乘法由 定义. 如果我们用矩阵来表示 和 ，就会有 这就是量子力学中无处不在的 对易子 (commutator) . 至于为什么李群间的元素要按照 中的规则来运算呢，可以这样来看：假如我们把 和 直接看成两个数，那就有 . 但是， 和 都是群 中的元素，而 却未必是群 中的元素. 我们从群的定义 (封闭性要求) 出发，同一个群里的元素结合后必须仍属于这个群，因此要像 中那样才能保证这个要求.

在稍微了解了李代数后，我们给出李代数的严格定义.

一个李代数是一个向量空间 加上一个二元运算 ，满足

值得一提的是，满足李代数 的二元运算有很多种，比如经典力学中的泊松括号. 现在你就可以看到为什么泊松括号和量子力学中的对易子有着隐约的联系了[4]，因为它们其实是两个同态群的李代数.

我们回忆一下，三维旋转 是这样定义的：

根据我们前文所说的李代数的特点，我们可以把群元素 写成 的形式，其中 就是 的生成子.

我们把 代入到 里，得到 如果我们用矩阵来表达 ，为了满足上面的两个条件，我们一般用以下这三个线性独立的矩阵： 这三个矩阵构成了 生成子的一个基，即任何一个生成子都可以被写成 的形式. 如果你对 Levi-Civita 符号比较熟悉的话，我们可以把这些生成子写成更简洁的形式：

你可以自行验证，我就不展开写了.

接下来，我们还可以利用李代数的定义 得到 然后你就会惊奇地发现，这里的 实在太像量子力学中的角动量算符了，但我们离角动量算符的对易关系之间还差一个 ，于是我们给它添上：在物理上，我们通常会给生成子 多乘上一个常量 ，这个做法实际上是要让生成子变成厄米 (Hermitian) 的，因为在量子力学中，厄米算符才有实的特征值.

也就是说，我们实际上会取 这样一来，由 我们有 这就是为什么我们要再乘上一个 . 于是我们就可以把李代数写成 现在就和我们学过的量子力学一致了！

我们回忆一下，引入 的时候，我们是想用四元数来描述一个三维旋转. 是这样定义的： 它是三维旋转 的二重覆盖[5].

首先，我们想要知道它的生成子应该满足什么条件. 和上面的 类似，我们先把生成子写成 的形式，代入 得到 对于满足以上条件的基，而我们通常取泡利矩阵 (Pauli matrices) 把这组基代入得到李代数 这里多出来的“2”就体现了 和 之间的二重覆盖关系. 为了让这条式子更好看，我们可以取 ，这样一来，它的李代数就是 这就得到了与 完全相同的李括号. 这就是为什么我们说 和 有相同的李代数 (我们是用李括号来定义李代数的) .

一个流形 是一个具有连续双射的点集，这些双射由集合内点的开邻域映射到一个开集 上. 形象一点理解就是，流形 在 局部上 看起来就和 一样. 这个映射利用一个 元组 将流形上的相邻的点“连接”在了一起，数 就称为“坐标 (coordinates) ”.

所以物理一点来讲，一个 维流形就是一个集合，这个集合中的任意一个点附近的位置都可以被 个独立的坐标所确定.

一个比较常见的流形就是一个二维球面. 一个二维球面就是一个三维球的表面，它被记为 . 而这样一个二维球面是通过点集 来定义的. 由于点集 提供了一个额外的限制，因此原本三个自由度的独立坐标 现在只剩下了两个自由度，所以 是二维的. 这也是为什么我们在数学上把 叫做一个二维球.

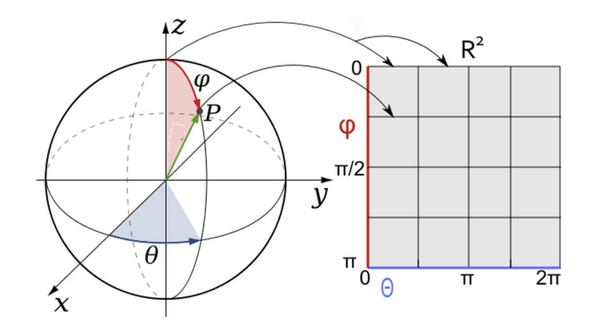
图1: 二维球坐标

我们把 上所有点的坐标的集合叫做 ，实际上这个 就是我们常见的球坐标 ( ) .

可以看到， 上的所有点都可以被唯一映射到 上的一个点 ，除了一个点—— 的那个极点. 显然这个在 上没有唯一的像点，整条 直线都是它的像. 因此，为了准确描述 这个位置，我们需要这个位置附近邻域内的点来描述它. 这就是为什么我们要求 必须是开集 .

稍稍了解流形后，我们终于可以给出李群的抽象定义了.

一个李群 就是一个可微的流形. 而群操作 就是由流形上的某个点到这个流形本身上的映射.

在李群的理论中，有这样一个定理：

每一个李代数都对应着至少一个唯一的李群.

现在我们有了流形的概念，我们就可以更好地理解这个定理了. 从几何上来说，这等价于：

每一个李代数都对应着唯一一个单连通的李群.

这个单连通的李群可以被理解成是一个“母群”，而其他拥有相同李代数的就是它的“子群”. 所有的子群都被母群所覆盖. 在前面我们多次提到， 是 的二重覆盖就是这个意思， 在 流形上覆盖了两次. 反过来说， 在 流形上正好占了一半.

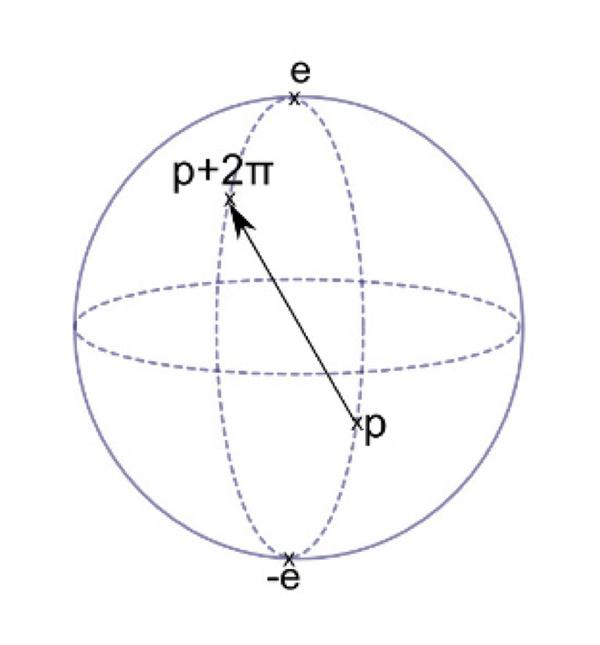
图2: SU(2)流形

我们在前面提到， 其实就是三维球 . 因为一个 上的点 对应着两个 上的点 ，所以我们可以把 理解为 的上半部分.

Coming soooooon ...