[前置内容] 从映射到张量
from 专栏 物理中涉及的数据处理方法
话题:
线性代数, 理论物理, 张量, 東雲正樹, 物理中涉及的数据处理方法
正文:
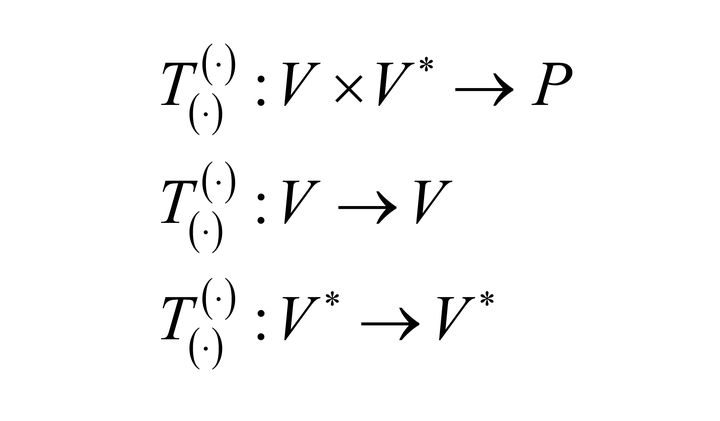
序言
对数学系来说可能写的太怪了, 是给物理人提供的代数基础速成系列. 就如果你是学物理的, 那这些知识就从头到尾都是要求彻底掌握的.
因为经常要用到相关概念, 每次写东西都简略介绍一遍的话既麻烦又不够完善, 但不提一下也不是. 所以就决定将这些基础的代数结构单独拎出来写一篇 note 来充当其它 notes 的前置内容.
本文最大的优点应该还是易懂吧, 但不保证能写得多么完美无瑕, 不敢说有多严谨. 只能说是我自己这么多年来都是这样看待这些概念的, 然后一直到今天也无出啥大问题. 现在只是把我的理解记录了下来供大家参考.
目録
1. 映射
1.1. 设集合
, 则可以定义集合间的映射
2. 线性空间与线性变换
2.1. 线性空间
2.2. 基矢
2.3. 线性变换
3. 内积空间与度规空间及二者的区别
3.1. 内积空间
3.2. 度规空间
3.3. 浅谈二者
4. 对偶线性空间
4.1. 对偶线性空间的本质是对矢量的全体线性映射构成的空间
4.2.与 上不存在自然同构映射, 但 与 上却存在
4.3. 选定了内积或度规后与 上就已经存在一个同构映射了
5. 张量与张量积
5.1. 张量是基于矢量与对偶矢量定义的概念, 对偶线性空间可由内积或度规确定
5.2. 张量的本质就是一台没有感情的多重线性映射机器
5.3. 常见的张量例子
5.4. 张量的退化
5.5. 是不是太抽象力? 我可以举一个极其具体的例子, 让你直观感受一下
5.6. 张量积的基本概念
5.7. 张量所处的线性空间
6. 令人心跳不已的指标运算
本文涉及的最基本的运算关系与逻辑符号的约定
(1). 符号
用于连接两个在特定数学概念上完全相同的内容.
(2). 符号用于连接两个在特定数学概念上有差异的内容.
(3). 符号用于代替词语 定义为 或 为 , 即其中一边是另一边的一个记号.
(4). 符号用于代替词语 存在 , 符号 用于代替词语 任意.
(5). 符号的左边是集合中的元素, 右边是元素所处的集合.
(6). 符号的左边是右边的子集; 符号 的左边是右边的真子集.
(7). 符号用于代替词语 可推得 , 符号 用来代替词语 对应于.
(8). 直积的作用是生成有序元素组的集合[1]: .
(9). 格式表示的是 被 作用的结果.
(10). 若内部有小括号则外部的小括号会自动升级为中括号, 如.
(11). Kronecker delta就是 和 两个数的简单记法.
1. 映射
1.1. 设集合
这个记号的意思是
是一个能通过输入一个 中的元素来得到一个 中的元素的映射.
✦ 映射
(1). 单射: 对
满足 [2].
(2). 满射: 对一定能找到一个或多个 满足 .
(3). 双射: 即集合间存在一个一一对应的关系.
若非满射的话, 值域
是 Image 的缩写, 显然满射可以表达为 .
✦ 单射加满射可以得到双射:
先引入
映射要求
是存在且唯一的, 即映射本身要求不能一对多且 全员参与,
对, 单射要求 是唯一的 (不要求一定存在), 即不能多对一,
对, 满射要求 是一定存在的, 即 内全员都参与这个映射活动,
所以 单射 + 满射 就可以给出两个集合间的一个一一对应的关系.
✦ *强行逆映射[3]:
对于非单射的情况, 即
可定义强行逆映射:
其中
是 的一个独点子集.
2. 线性空间与线性变换
2.1. 线性空间:
✦ 线性空间
上述中的
是数域, 参与数乘的数就属于数域, 可以是实数域 或复数域 等[5].
要注意到顺序是这样的:
我们是先给定了一个数域,
然后才给定一个集合,
集合内定义一个 的二元运算, 称之为矢量加法,
然后定义一个的数乘运算将 与 耦合起来.
所以谈线性空间的时候要指出是什么域上的线性空间.
✦ 矢量加法
下面对
(1). 矢量加法的交换律:
.
(2). 矢量加法的结合律:.
(3). 存在零元, 即矢量加法的单位元使得 .
(4). 存在矢量加法的逆元使得 .
(5). 存在数乘的单位元使得 .
(6). 数乘与数域乘法相容:.
(7). 数乘对数域加法的分配律:.
(8). 数乘对矢量加法的分配律:.
注意数乘是不要求交换律的, 然后就是数域自带了正常的乘法和加法, 就是小时候玩的那种.
✦ 举一例加深理解[6]:
在
若将
定义为矢量的加法, 而将 定义为数乘的话 就构成 上的线性空间.
✦ 最后, 由于矢量加法与数乘的运算与数域加法乘法相容, 就没必要特意创造新符号了.
就是说我们将用
与 来代替 与 , 这并不会造成任何混乱.
2.2. 基矢:
✦ 线性无关与线性相关:
若存在不全为
的一组数 能使 个矢量 > 满足 则称这组矢量是线性相关的.
若不存在则说明上述个矢量 是线性无关的.
就是说如果
✦ 线性空间
实际上,
所以两个线性空间只要维度相同我们就可以说它们同构[7]了.
二者同构的数学定义是二者之间存在一个同构映射, 后面讲到对偶空间时会再提一下.
✦ 当你找到了
你决不可能再从线性空间中找到一个与这个集合达成线性无关条件的矢量了[8].
那么反过来说现在对
都一定存在一组不全为零的 > 使式子 成立.
移项可得, 说明任何矢量都可以被 线性展开,
于是我们就称为基矢.
任何
但将来我们会选择其中最讨人喜欢的那些标准正交基, 现在还无法定义, 后面会说.
2.3. 线性变换:
✦ 线性变换
关键在于是 线性 的映射, 就很好算, 线性就是说对
(1).
.
(2)..
那再提一嘴, 用到复数域的时候, 我们说的 线性 有时是在指 反线性 :
(1).
.
(2).[9].
比如复线性空间到对偶空间的同构映射就是反线性的.
其实都大差不差啦, 所以很少会专门强调这个事儿.
3. 内积空间与度规空间及二者的区别
3.1. 内积空间:
✦ 内积空间就是定义了内积运算的线性空间, 内积本质是一个映射
即对
有 . 而这个映射是人为指定[10]的, 并没有什么玄妙的地方.
然后就是上述映射要满足以下四个条件才能被称作内积运算:
(1).
[9].
(2)..
(3)..
(4)..
✦ 内积空间中对
有了内积就可以定义 标准正交基 为两两内积为
且模长均为 的矢量构成的一组基底.
3.2. 度规空间:
✦ 度规空间就是指定了度规的线性空间, 度规的本质是一个双线性映射
即对
有 .
然后就是度规需要满足的要求:
(1). 对称性: 对
有 .
(2). 非退化性[11]: 即若对均有 则可推知 .
✦ 度规空间中对
有了度规就以定义 标准正交基 为两两度规作用为
且平方均为 的矢量构成的一组基底.
3.3. 浅谈二者:
✦ 首先二者不存在包含关系, 数学不会这么无聊, 但细究起来二者的差异又十分微妙.
以至于你去问几乎身边任何一个物理人, 他们都会说「这只是同一个东西的两种写法罢了. 」
靠谱一点的物理人考虑到复共轭的问题后会说度规可以都用内积刻画, 然而他还是错了.
另一种靠谱的物理人考虑到相对论后可能会说内积都可以用度规刻画, guess what[12]?
所以实际上一个云里雾里的物理人照样能做物理, 细节清晰度仅取决于你对自己的要求.
✦ 退回到三维欧氏实空间去看, 俩矢量做点积究竟该视为内积映射还是度规作用?
答曰都可, 然而 generally 来说区别还是存在的:
(1). 内积空间要求
, 即矢量的模有非负性, 而度量空间中并无此要求[13].
(2). 内积涉及取复共轭而度规作用 是对称的.
前者导致内积无法表达平方为负的情形, 后者导致度规无法表达内积的取复共轭操作[14].
4. 对偶线性空间
4.1. 对偶线性空间的本质是对矢量的全体线性映射构成的空间:
✦ 记线性空间
换句话说就是
中的元素也叫 中矢量的线性泛函[15].
✦
蛮容易证明的:
我们只要先任选
中的一组基矢 .
则总可以通过条件[16]找到一组 .
结论就是一定构成 的一组基底, 它们也被称为 的对偶基底.
就是说对都可以做展开 , 其中 全都是系数.
这就归结为只需证明对偶空间中的任意元素 都存在 形式的展开式:
我们首先定义系数.
再令待证式两边同时作用于基矢 , 左边为 .
右边为, 于是左边 右边.
上述关系对所有基矢都成立, 即对全体矢量都成立, 故得证.
关于最后那一步再讲细一点儿罢:
前面就是证明了作用在任何一个矢量上都与 作用在该矢量上的效果相同.
这是因为每一个矢量都可以被基矢线性展开, 而作用在每个基矢上的效果都是相同的,
最后考虑到是一个线性的映射所以就可以说 与 作用在矢量上效果相同了.
4.2.
✦ 所谓自然同构就是一个与众不同的映射, 它是如此的出众, 以至于大家都会自然地选择它.
两个同维的线性空间, 肯定可以在二者之间建立一个线性双射, 即称之为同构映射.
前面我们通过条件
由一组 的基底生成了一组 的基底.
这个基底的对应关系就可以用来建立一个间的同构映射,
比如说可以将都同构映射到一个与之对应的 上.
你会发现这个同构映射的建立是依赖于中的基底选取的, 这个选取是纯人为的.
假如我们一开始选择的是中的另一组基底, 则 中生成的对偶基底也会随之而变.
此时同构映射也就变了, 但这两个同构映射显然是平权的, 故这里没有最自然的选择.
或者在同样一组基底与对偶基底下, 你也可以换一个对应方式, 比如对应到 之类.
这样得到的到 的同构映射也是个不同的映射.
一般来说一个同构映射并不只是一个双射, 通常还要要保这个保那个的,
比如说群同构或者代数同构都要保相应的「乘法」, 但线性空间实在是结构太简单了,
所以线性空间之间的同构映射就只是一个建立在二者基底之间的线性双射罢了.
但
显然
作为一个线性空间自然也有权产生一个对偶空间, 即 .
我们说的就是与 之间存在一个最自然的同构映射.
由对偶空间的定义得对 都有 ,
那完全可以定义映射使得对 都有 .
显然其中的作用对象 是 中的元素, 而 按定义来看则属于 .
这样, 如果我们将与 对应起来, 这个映射就是自然的、独一无二的、可分辨的.
这就是为什么我们不会再研究
由于自然同构映射的存在,
完全可以视为 本身, 更多 的那些空间自然更不用说了.
4.3. 选定了内积或度规后
内积本质是一个映射
而这里说的已经存在的同构映射就是对
> 都可以通过内积唯一地同构映射到 > 其中的 指的是填了一个矢量的内积括号, 这样再填一个矢量就会给出一个数字,
所以这实际上是一个矢量空间到数域的线性映射, 既一个对偶矢量.
在这样一个确定的内积下, 我们还可以选一组特殊的基底, 即标准正交基[17].
标准正交基会满足关系 .
显然我们已经找到了对偶空间的基矢.
因为这样的的基矢 会满足关系
所以实际上内积或度规的选取与
5. 张量与张量积
5.1. 张量是基于矢量与对偶矢量定义的概念, 对偶线性空间可由内积或度规确定:
✦ 定义一个数域
想诱导出对偶线性空间只需找到一个
✦ 这个映射一般选择内积
内积运算
显然我们可以用很自然地利用内积建立一个单射
定义符号
那么 满足什么性质呢?
我定义它满足对有 , 即 .
说玄乎点就是一个线性泛函, 意思是它作用到矢量上会给出一个数.
显然这样一来我们就构建了一个与同构的对偶空间 .
即对, 必 与之对应, 而 里的元素就是对偶矢量.
5.2. 张量的本质就是一台没有感情的多重线性映射机器:
✦ 张量是如此地冷酷, 你只要把足够矢量和对偶矢量投入这台机器, 它就会给出一个数.
✦ 其实张量有无数多种, 但可以按照出数所需投入的矢量与对偶矢量的数目进行分类.
比如说 (1,1) 型张量就是投入
我们可以将 (1,1) 型张量记为
, 它对 有 .
用映射的语言来说, (1,1) 型张量就是双线性映射.
比如说 (0,1) 型张量就是投入
我们可以将 (0,1) 型张量记为
, 它对 有 .
用映射的语言来说, (0,1) 型张量就是线性映射.
比如说 (2,1) 型张量就是投入
可以将 (2,1) 型张量记为
, 它对 有 .
用映射的语言来说, (2,1) 型张量就是三重线性映射.
还需要注意的一点是与 不一定相等.
✦ 关键点: 具有两类输入槽, 一个输矢量一个输对偶矢量, 每个槽都是线性的 [18], 输满就出一个数.
聪明的你, 一定不需要我再继续比如了吧, 比如说当然可以有 (114, 514) 型张量啊.
5.3. 常见的张量例子:
✦ 矢量和对偶矢量分别可以视作 (1,0) 型张量与 (0,1) 型张量 and vice versa.
对偶矢量
的定义不就是对 有 吗?
这显然就是 (0,1) 张量的定义嘛.
矢量如何看作 (1,0) 型张量呢? 重点在于如何定义让它能作用到对偶矢量上.
其实很简单, 对都定义 不就是了吗?
✦ 线性变换
线性变换就是将一个矢量映射到另一个矢量对吧? (1,1) 型张量呢?
按定义来说 (1,1) 型张量的作用是将一个矢量和一个对偶矢量一起映射到一个数.
写出来就是, 若我们就只输入一个矢量 呢?
那么对来说是不是再来一个对偶矢量就得到一个数? 即 .
这就说明投入了一个矢量使 (1,1) 张量退化为 (1,0) 型张量了.
而 (1,0) 型张量不就是矢量吗? 所以我们是往 (1,1) 张量里投入矢量后得到了另一个矢量.
而从这个角度来看 (1,1) 型张量就是这样的映射, 这不正是线性变换吗?
✦ 度规是一个 (0,2) 型张量: 度规的本质是一个线性映射
✦ 从这个角度来看, 矢量和对偶矢量就都是张量的特例. 它们虽然不处于同一个空间, 但它们所处的空间都是由同一个空间衍生出来的.
5.4. 张量的退化:
✦ 以 (2,3) 型张量
即
这就是一个 (2,3) 型退化为 (2,1) 型的过程, 我想这个是很显然的事情就不赘述了.
5.5. 是不是太抽象力? 我可以举一个极其具体的例子, 让你直观感受一下:
✦
✦ 线性空间
这是显然的, 矢量就是线性空间中的元素嘛.
✦ 线性空间
对偶矢量是对偶线性空间
中的矢量, 本质是 的线性映射.
而行矩阵通过矩阵乘法可以将任意列矩阵唯一线性地映射到一个数.
前面我们提到的对偶映射在这里就是转置运算.
能如此顺利是因为实列矩阵空间中对天然地就定义了内积 .
✦ 线性空间
从定义出发, (1,1) 型张量就是双线性映射
.
前面我们证明了它同时也可以看作线性变换.
上述两个映射映射观点的等价性在这个例子下也很直观:
方阵结合矩阵乘法可以通过右乘一个列矢量来得到一个列矢量, 此即.
方阵左乘一个行矢量右乘一个列矢量可以得到一个数, 此即.
5.6. 张量积的基本概念:
✦ 我们用符号
✦ 自然可以有线性空间之间的张量积
要办到这一点应该怎么做呢? 按定义可知从映射角度来看有
.
我们给出的做法如下:
(1). 先在中找一组基底 .
(2). 再在中找一组基底 .
(3). 然后定义集合.
(4). 用上述集合内的元素作为基矢所张成的线性空间就是.
另外线性空间内的基矢之间与张量积相关的运算还有这样的性质:
(1). 基矢的加法满足> (2). 数乘满足 .
对于这样的它就等于 , 不能再分解了.
你发现这些性质很像乘法的分配律, 所以这玩意儿叫张量 积 嘛.
值得一提的是
具体而言就是并非对
都存在 使得 .
不多说嗷, 对于不能分解的在量子力学上还专门起了一个名字叫纠缠态, 懂得都懂.
5.7. 张量所处的线性空间:
✦ 上一节我们讲的张量积有点儿离题, 但比较 general, 像 QM 里用的就是那种[21].
✦ 接下来我们要介绍的就是前面定义的那些个张量所处的空间.
为此我们要先对
这样一来,
就都是 (1,0) 型张量, 就都是 (0,1) 型张量.
我们要求, 即相当于 .
具体的映射方式可以规定为.
这样相当于可以通过张量积将 (1,0) 型张量与 (0,1) 型张量拼成一个 (1,1) 型张量.
显然两个 (1,1) 型张量的任意线性组合仍是一个 (1,1) 型张量:
即.
那如何找到所有可能的 (1,1) 型张量呢?
显然只需要用做基底张成一个线性空间即可.
然后这个线性空间里的矢量全都是我们要找的上的 (1,1) 型张量.
我们前面已经证明了矢量的线性映射构成的空间与线性空间同维[22].
那么 (1,1) 型张量作为双重线性映射自然就是
维空间的元素.
从基底的数目也是 个来看,
上述基底张成的空间里不仅全是 (1,1) 型张量, 更应该是包含了所有的 (1,1) 型张量.
其实也不用这么看, 很显然所有的 (1,1) 型张量都必须被上面那些基矢展开, 因为对偶矢量空间的定义本身就是矢量空间上的所有线性映射的集合嘛.
基底
所以说 (1,1) 型张量的空间就是
.
可以用此基底展开任意 (1,1) 型张量其中 .
要证明这个很简单, 只需等式两边同时作用在上即可, 此时左边 .
右边则是即得证.
✦ 这个结论很容易推广到任意型张量, 下面给出结论:
全体
前面我们说矢量和对偶矢量都是张量的特例, 但从这个角度来看张量又是矢量的一个特例.
6. 令人心跳不已的指标运算
对矩阵有一种张量积的特例, 叫克罗内克积, 想进一步了解请参考:
[1]: 这个也叫 Cartesian product, 说白了就是打包处理, 并没有给予任何额外的操作.
[2]: 其实数学人口中的嵌入基本上就是单射的意思, 一旦接受这种设定之后你会发现嵌入这个词其实比单射要传神一些.
[3]: 估计要学微分几何才用得到.
[4]: 我之所以不用普通的加号和乘号就是为了让大家意识到, 这里说的加法和乘法与数域中的相应概念不完全是一回事. 只要是能满足下面的八条运算规则的就都有资格充当这俩运算. 当然日常生活中不会这么写, 这是因为下面八条运算规律让数域上的加法与乘法和矢量加法与数乘相容了.
[5]: 呃··· 与其说可以是不如说只能是, 物理人难道还真的用得到这俩之外的域吗?
[6]: 如果你能证明下面说法, 你应该就算很懂线性空间是怎么一回事了.
[7]: 同构, 就是存在一个结构上的一一对应. 两个事物同构就是说两个事物在作为特定的数学对象 (比如说线性空间) 来考虑时是完全一样完全等价的.
[8]: 要真找到了无非就是维度喜加一, 说明你前面找的还不是最大的呗.
[9]: 右上角星号表示取复共轭.
[10]: 只需要指定基矢之间的映射效果就好了.
[9]: 右上角星号表示取复共轭.
[11]: 这里给出的定义比较玄乎, 其实度规本质上是线性空间上的一个 (0,2) 型张量, 选定一组标准正交基后可以排列成一个矩阵, 若该矩阵的行列式不为零则可称这个度规是非退化的.
[12]: 他还是错辽.
[13]: 一个显然的例子就是, 在相对论时空下, 我们取了洛伦兹度规, 此时的矢量就会根据其平方值大于零, 等于零, 小于零三种情况分为类时, 类光, 类空三种矢量(洛伦兹度规也分两种等价的号差, 所以这仨矢量名称的用法并不统一).
[14]: 但如果你去掉内积映射的非负性要求, 定义一个「广义内积」的话, 那我想广义内积应该就包含了内积与度规作用了.
[15]: 相信大家都听过泛函这个词, 就是函数到数的映射对吧? 这里明明是矢量到数的映射为何也叫泛函呢? 这是因为映射作为矢量其实也可以构成线性空间, 比如所谓的平方可积函数空间.
[16]: 必须通过这个条件来选, 否则你在对偶空间生成的基底就不能叫原线性空间的对偶基底了, 且一定还会为后续的工作造成许多混乱.
[17]: 其实你也可以先选好基底, 然后总可以再通过选择一个恰当的内积映射使这组基底为标准正交基.
[18]: 因为很简单所以我很少展开讲这点, 但千万别忘了, 这点超妈重要.
[19]: 这里的实指的是 V 是实数域上的线性空间.
[20]: 我印象中一般都是同一个数域上的俩线性空间才搞这个张量积. 数学人好像管这个叫扩张? 我知道这个听起来很瑟琴, 但他们好像真的就是这么叫的.
[21]: QM 里大家都管这个叫直积, 这个狗屁叫法让张量积与笛卡尔积完美地混淆了起来. 平时跟老师讨论问题也是, 大家都知道这么说不对, 但就忍不住, 可以说是满口黑话了.
[22]: 未加说明时一般默认我们讨论的线性空间是 n 维的.
评论:
规范玻色子:
令人心跳不已(×)
令人心肺停止(✓) (36 赞)
脉冲星: 国内大学教的线代也就图一乐,真学线代还得看🌴 (30 赞)
知乎用户: 突然发现一节课看这个物理用文章能补上至今为止上的所有线代课的内容. (21 赞)
南方锂合金: 没有废话,全是干货。实际上不学不知道,学了之后才发现物理里常用的那部分线性代数和基本的泛函知识根本没有想象中那么晦涩难懂😂 (13 赞)
Radius: 论阿树的文章从刚入学看到快毕业,,, (11 赞)
亲口吃梨:
5.7中 显然两个 (1,1) 型张量的任意线性组合仍是一个 (1,1) 型张量的下一行,等式左右不相等吧。等式左边展开的话,还有多余的项 图片 (7 赞)
東雲正樹 -> 亲口吃梨: 啊, 确实. (3 赞)
溜溜子: 高三就看到这篇文章,学完Axler的线代之后终于能看懂了[大哭] (3 赞)
東雲正樹 -> 溜溜子: 当时哪儿不懂❓
溜溜子 -> 東雲正樹: 对偶那一块,还有自然同构,现在发现自然同构是done right 上的一道习题 (1 赞)
東雲正樹 -> 溜溜子: 那不就是全部? 你现在还能理解你当时为啥不理解吗?
溜溜子 -> 東雲正樹: 好吧,按照这个意义上来说,当时我完全没懂[大哭]
zgedphlie: 睡不着的时候看看树桑的文章😳 (5 赞)
Wanghengheng:
每次认真地看树的文章都有突然袭击的114514……
😱😂 (4 赞)
secret c: 好臭的张量🐕 (2 赞)