title: 物理学中的群论 · 入门篇 第一章:有限群
permalink: https://zhuanlan.zhihu.com/p/539510930
author: Frank Hua
author_id: fb6f6991d7cf973c43e94f6319554b6d
column: 物理学中的群论 · 入门篇
column_id: c_1532040361488310273
voteup: 182 赞同
created: 2022-07-22T15:54:49
updated: 2022-09-20T19:57:41
fetched: 2024-05-17T21:08:53
count: 约 10397 字
version:
tags: [物理学, 数学, 理论物理, Frank-Hua, 物理学中的群论-·-入门篇]
url: https://zhuanlan.zhihu.com/p/539510930
物理学中的群论 · 入门篇 第一章:有限群
from 专栏 物理学中的群论 · 入门篇
话题:
物理学, 数学, 理论物理, Frank-Hua, 物理学中的群论-·-入门篇
正文:
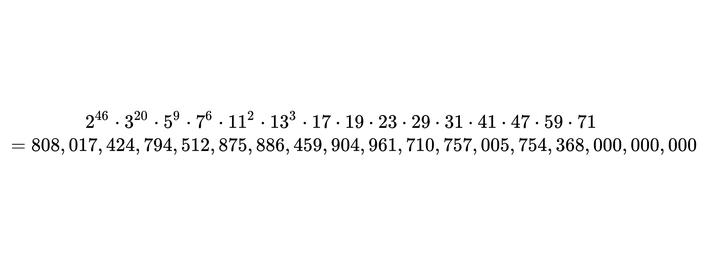
系列目录 :
物理学中的群论 · 入门篇 第〇章:概述
物理学中的群论 · 入门篇 第一章:有限群
物理学中的群论 · 入门篇 第二章:有限群表示论
(未完待续 ······ )
这一章主要介绍 有限群 的基本性质,之所以上一章是“第〇章”,是因为从这一章开始才有真正的内容1. 从本章开始,对于简单的性质定理将给出简要的证明,复杂的定理将直接给出或者只提供直观理解的方法(物理版群论就是突出一个直观理解).
重复一遍有限群的定义: 群元素为有限个的群就是有限群. 对于初学者而言,有限群较为容易接受(虽然某些性质可能比
一、有限群的描述:如何给定一个群?
既然把群分类研究,那说明有限群和
给定了所有群元之后,此时就只需要确定群乘法. 群乘法可以一般地记作

有限群的群乘法表
其中每一行表示左乘群元,每一列表示右乘群元. 这就是有限群的 群乘法表. 一旦给定了群乘法表,有限群的一切信息都完全给定了.
二、例子:几个简单的有限群
既然低价的群往往较为简单,我们就先考察几个低阶群的结构:
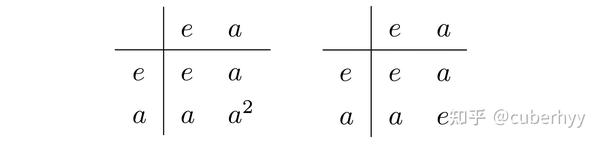
二阶群乘法表
- 三阶群. 从三阶群开始,为简单起见,将直接给出群的结构而不再仔细分析如何导出,感兴趣的读者可以自行推导8. 三阶群和二阶群一样,仍然只有一种群结构,并且仍然只有一个生成元(秩为
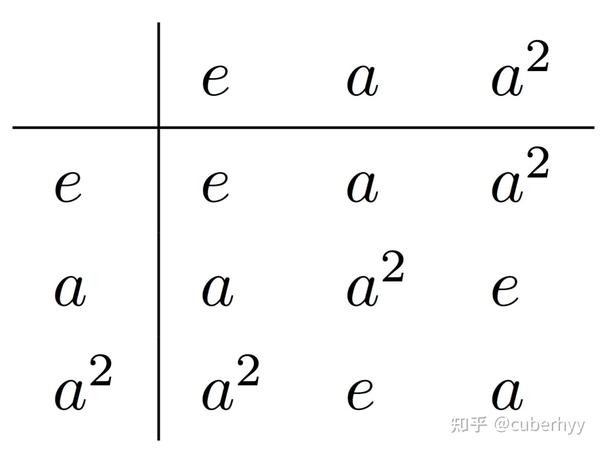
三阶群乘法表
- 四阶群. 从四阶群开始,情况就稍显复杂起来. 不同于二、三阶群,四阶群拥有两种不同的群结构. 第一种结构依然只有一个生成元,还是记作
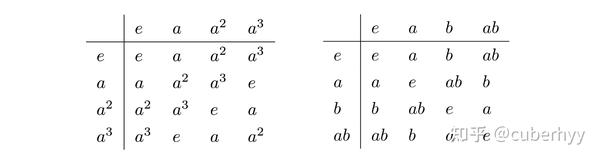
两种四阶群的群乘法表
以上的群是按照群的阶来分类来讨论群的结构,但正如四阶群的例子所示,同阶的群可能拥有截然不同的结构,进一步拥有不同的性质,因此不能一概而论. 更合理的分类方式应该从 群的结构 入手.
- 循环群
- 二面体群

D3群的群乘法表
最后强调一下,这里给出的群,都只关心群的结构,而不关心群元的具体内容,所以(比如)
三、有限群的主要性质——感受数学的神奇
虽然群乘法表已经完全确定了一个有限群,但实际上我们研究有限群主要是试图理解它的各种性质,从而引出各种应用. 所以本部分的重点就是介绍有限群的主要性质.
3.1 群乘法表的性质
既然一个有限群所有的性质都包含在群乘法表中,我们首先考察群乘法表本身有何性质,在此基础上可以更方便地构造出一个群的乘法表.
- 观察上述
- 如果一个群是阿贝尔群,那么任意两个群元的乘积满足交换律. 表现在群乘法表上的特征为:乘法表主对角线均为单位元;乘法表关于主对角线对称. 因此只要判断出一个群是阿贝尔群,构造乘法表的工作量直接减半.
- 例:可以观察上述二三四阶群(均为阿贝尔群)的乘法表,显然关于对角线对称.
3.2 有限群的各种子集
如果一个群太复杂,不便于直接看出其性质,我们不妨转而研究它的子集,进而得到群的部分性质. 这一部分将介绍有限群的几种重要子集以及由此导出的性质. 而对于群来说,一种重要的子集就是子群(定义见上一章),我们首先看看子群有没有什么性质. 为此,我们引入一个新概念:
- 陪集 :设待研究的群为
- 例:以
- 例:以
陪集有几个重要性质10:陪集必不是子群;陪集与对应的子群没有公共元素;陪集中没有重复元素;不同的陪集没有公共元素. 也就是说,利用陪集可以由子群生成一个新的子集,并且选取不同的群元
- 给定一个子群
- 任选一个群元
- 将子群与上述左陪集合并,得到新的集合
- 再选取另一个不属于
- 重复步骤4,直到集合
由于不同的陪集没有公共元素,上述过程的存在说明我们可以将任意一个有限群
由这个性质还能得到另一个结论:如果群的阶为质数,那么它就不包含任何非平庸子群12,也就不能拥有任何子结构, 只能是最简单的循环群 !例如
既然陪集分为左陪集与右陪集,那么存在两种情况:左陪集与右陪集不相同; 左陪集与右陪集相同. 后者看起来比较特殊,值得研究一波. 于是引出下面的定义:
- 不变子群 :如果一个子群所有的左陪集与对应右陪集都相同,我们称这种子群为 不变子群 ,有的教材也称之为正规子群.
- 例: 以
- 例: 以
这种特殊的子群在有限群结构的分析中有着至关重要的地位,下一部分会给出相关的性质. 这里首先讨论 如何找到一个不变子群. 不变子群的定义可以表述为:对于任意
- 共轭与共轭类 :对于两个群元
- 例:仍以
- 共轭类的性质:与子群类似,任何一个共轭类中元素的个数都是群阶数的因数.14 这也是一个惊人而美妙的结论.
- 阿贝尔群的共轭类:在阿贝尔群中,
- 例:仍以
不变子群和共轭类具体有何关系?由不变子群的定义可以看出,如果某不变子群
3.3 复杂群的分解
对于一个有复杂结构的群(例如
- 寻找同态—— 商群. 设群
- 例:
- 例:
如同常规物质由分子组成,分子有原子组成,原子由核子、电子组成,核子由夸克组成一样,有限群也可以逐级分解,比如上述例子中将
- 有限群的“基本粒子”—— 单群. 直观上来讲,单群作为有限群的“基本粒子”,就是指不能进一步分解的群. 严格来说,如果一个群除了本身和一阶群以外没有其他“非平庸”的不变子群,那么就把这个群称为 单群.
- 例:质数阶循环群
- 例:质数阶循环群
有了单群的定义后,我们自然地就会想知道,一共有哪些有限单群?这就像粒子物理中的标准模型、化学中的元素周期表一样,有着十分重要的地位. 而且这个看似简单的问题有着复杂到惊人的结论,花费了数学家们几十年的时间,使用了计算机辅助的机器证明,直到2008年才彻底解决. [17] 这个问题的答案被描述为下述定理:
- 有限单群分类定理.[18] 所有有限单群均属于下列四大类中的某一小类:1. 质数阶循环群
- 的群. 分类的具体内容详见: 有限单群列表
值得注意的是,在26个散在单群中,有一个群格外显眼,它有808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000阶,也就是大约
找到所有的“基本粒子”之后,接下来自然的问题就是非单群是如何分解成单群的. 这就像是研究非基本粒子是如何由基本粒子组成的. 首先引入记号:
- Jordan–Hölder定理 :如果上述分解中商群
- 例:对于
- 例:对于
至此我们就从原则上给出了所有的“基本粒子”——单群以及将任意有限群分解为单群的方式,有限群理论的框架已经基本完备.[21]
上一章 :第〇章
[17]: 参考文献:维基百科
[18]: 这一部分属于科普介绍性质,因为这玩意相关的文献加起来有上万页
[19]: 本系列第三章会介绍什么是交换群
[20]: 严格来说不唯一,但是各种分解方式是等价的
[21]: 其实还有很多丰富的内容,但对于物理系学生,尤其是初学者来说,本章内容已经过于充实
评论:
Frank Hua: 这波是真没人看了😱 (2 赞)
Cauchy -> Frank Hua: 👍
fhw -> Frank Hua: 再看,也在学习,只不过没有回复 (1 赞)
对称群小木子 -> Frank Hua: 22年的文章,24年还有人看呢[抱抱]
fhw -> 对称群小木子: 😱学无止境 (1 赞)
知乎用户:
陪集部分内容是直接从定义推出应用,完全不知道这样的变换折腾有啥意义,看起来毫无兴趣。
群分割有何应用价值,没事儿分割它干嘛,其他分割方式难道不行吗?闭着眼睛就一刀砍两半,到底比这种方式分割差在哪儿?
这个东西如果是后面的一个重要概念,那么后面不看也罢。
如果是科普读物,这样写,这个系列在这里就结束了。
如果是类似辅助科班学生理解的读书笔记之类,那这么写还可以,反正正经知识有老师辅导。
建议先有使用场景,遇到问题,然后用朴实的方式解决,接着再讲道理,再拓展应用,比较优劣,最后是使用局限,和常用场景。
这也是写科普的最有效方法。
Frank Hua -> 上官人: 这肯定不是科普😱
上官人 -> Frank Hua:
我其实很迷惑你写这东西的目的是啥,教辅材料?
你用了一个教科书式的写法,但是你的资历又不是能写教科书的专家,读者看你的东西是为了啥呢?
数学是工具啊,一个工具脱离了使用场景谈改进,这玩意儿除了学生自己花了钱为了学位不得不学,还有谁看啊?
我最开始看你的自我介绍,以为你是草根,结果你写的东西是官媒权威专家才用的教科书式写法,你又没有官媒天然的权威,必然没有流量,你写这东西是纯兴趣吗?
我纯兴趣就像你这么写,但是给甲方爸爸写就按照我上面说的写。
Frank Hua -> 上官人: 你是怎么刷到这篇的,知乎数学物理圈不都是这样吗😂
Frank Hua -> 上官人: 有没有一种可能,这种东西确实有人看(看评论区)
Frank Hua -> 上官人: 鉴于您对数学有如此肤浅的理解,我只能建议您尽量少在自己不熟悉的领域发表观点。
粥兑酒 -> 上官人: “读者看你的东西是为了啥”:那不就是因为想在不同的地方看看这个知识怎么讲,而如果看一本书想专门看这一部分会比较麻烦(比如这两本书讲的方式不同,切入角度不同),知乎在这方面就十分好,有许多人分享笔记和想法;再者当你完全认为这套理论自然的时候,很可能不能体会到初学者的困惑。“数学是工具”令人捧腹。最后谈一句,我认为多写这种材料是对中文学术环境有贡献的,如果许多东西不得不看外文效率还是会比较低。
查勃多得了如是说: 所有的陪集构成群的一个划分对不对?
Frank Hua -> 查勃多得了如是说: 一个子群和它的所有陪集构成一个划分
查勃多得了如是说 -> Frank Hua: H的所有陪集构成G的一个划分吗?
Frank Hua -> 查勃多得了如是说: H和H的所有陪集构成G的一个划分 (1 赞)
Frank Hua -> 查勃多得了如是说: H的陪集里面没有H本身 而所有的陪集都没有单位元 肯定要把H算进来才能构成一个划分 (1 赞)
查勃多得了如是说 -> Frank Hua: 谢谢解释,我大意了。
今夜满天星: 有人看👍 (3 赞)
Frank Hua -> 今夜满天星: 🧡🧡🧡 (2 赞)
砂糖橘好耶: 我的本科课程都是靠知乎大佬接济的[大哭] (2 赞)
fhw -> 砂糖橘好耶: 一样[酷]
小目: 写得很好,比我买的书,容易懂!😝 (2 赞)
Frank Hua -> 小目: 感谢支持👍
陈少林: 写得很好👍,期待更新! (2 赞)
乔老爷: 写得太好了!期待更新! (2 赞)
王赟 Maigo:
想问下,D3 的合成列也可以是 D3 ⊳ C2 ⊳ {e} 吧?
把 D3 分解成 C2 和 C3,这里面 C2 和 C3 的地位是不是相同的?
王赟 Maigo -> 王赟 Maigo:
呀,发现自己错了,C2 并不是 D3 的不变子群,所以只能是 D3 ⊳ C3 ⊳ {e}。
不过还发现,C6 倒是有两种可能的合成列:C6 ⊳ C3 ⊳ {e},C6 ⊳ C2 ⊳ {e}。
同样是 C2 和 C3,居然还能合成出 D3 和 C6 两个不同的群……
Frank Hua -> 王赟 Maigo: 确实,正准备回呢就看到您自己发了😱
带上狗狗去旅行: 左右陪集一个是rs一个是r²s这是写错了还是为什么这样写 不太懂 请解释一下
Frank Hua -> 带上狗狗去旅行: 这俩本来就不一样 根据前文的群乘法表可知sr=r²s
35SiO2 -> Frank Hua: 还是没整懂陪集😱,右陪集这个r²s怎么来的?