如何理解三大微分中值定理？ - 马同学的专栏 马同学高等数学

数学, 高等数学, 微积分

微分中值定理是很重要的基础定理，很多定理都是以它为基础进行证明的。

1 罗尔中值定理

1.1 直觉

这是往返跑：

可以认为他从 点出发，经过一段时间又回到了 点，画成 （位移-时间）图就是：

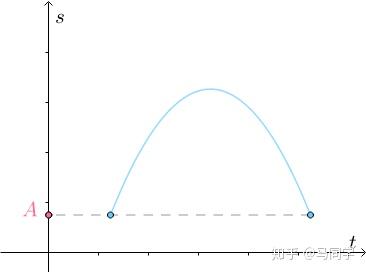
根据常识，因为要回到起点，中间必定有速度为0的点：

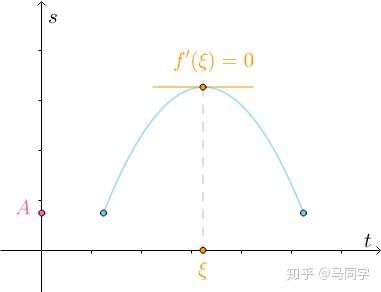
拳击比赛中，步伐复杂：

但不论怎样，只要最后回到起点，中间必定有速度为0的点：

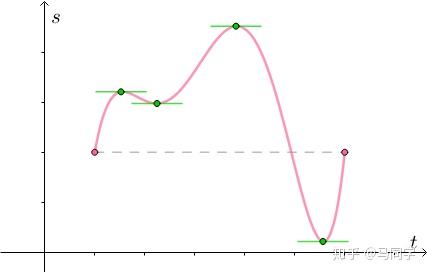
这就是罗尔中值定理。

1.2 罗尔中值定理

设函数满足以下三个条件：

• 在闭区间 上连续
• 在开区间 上可导
• 

则存在 ，使得

在闭区间 连续是必须的，否则有可能没有 ：

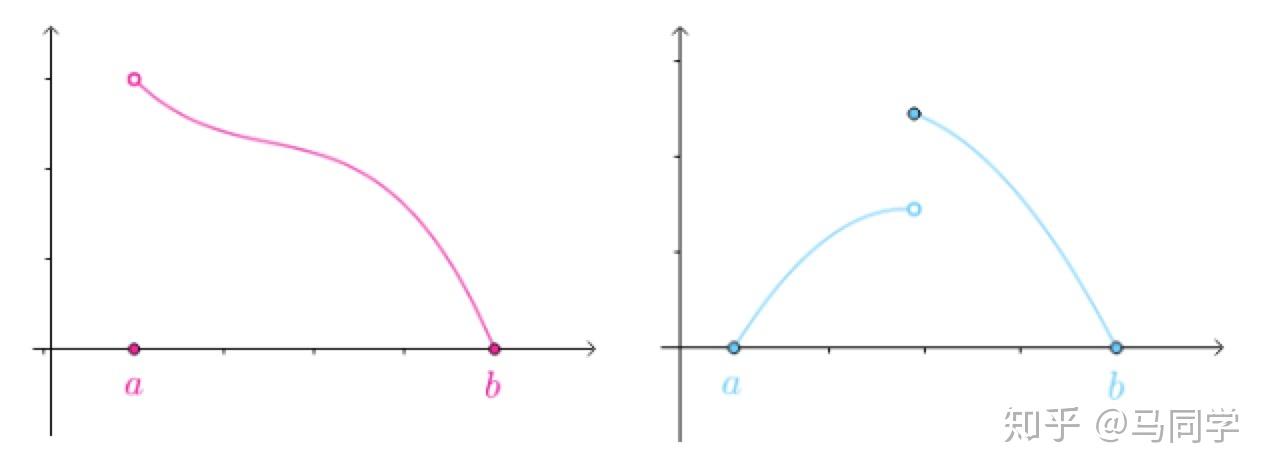
在开区间 可导也是必须的：

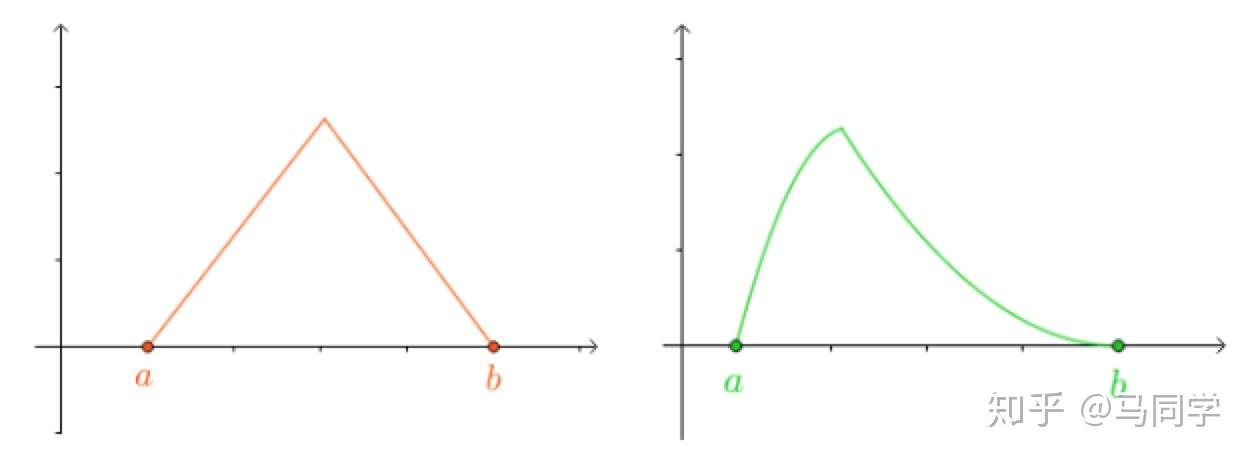
1.3 拓展

可能有的同学觉得，定理中的条件“ 在闭区间 连续、在 可导”比较古怪，为什么不是“ 在闭区间 连续、在 可导”？

大概有两个原因，首先，“开区间可导”条件更弱，包含了“闭区间可导”；其次，”开区间可导”的函数并不一定就“闭区间可导”，比如：

此函数在图像如下：

此函数就是在 连续， 可导，在端点 处导数不存在（类似于在0点处不可导，可自行证明）。

2 拉格朗日中值定理

来看下交通管理中的区间测速：

时间 采集到汽车的位移为 ，时间 采集到汽车的位移为

可以据此算出平均速度为：

比如算出来平均速度为 ，平均速度是由瞬时速度叠加的结果，那么路程中的瞬时速度可能为：

• 匀速前进：那么整个路程的瞬时速度必然全为
• 变速前进：整个路程的瞬时速度必然有大于、等于、小于 的情况

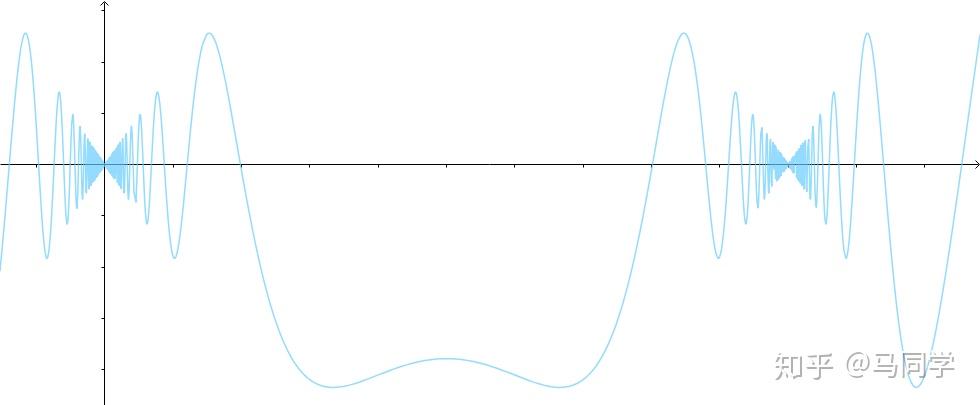
下面是变速前进的速度变换动画（蓝色为大于，闪烁为平行即等于，绿色为小于）：

如果限速 ，那么根据汽车的平均速度为 ，就可以判定路程中必然至少有一个点超速。

约瑟夫·拉格朗日伯爵，法国籍意大利裔数学家和天文学家，以他命名的拉格朗日中值定理就可以在数学层面解释刚才的现象。

2.1 拉格朗日中值定理

设函数满足以下两个条件：

• 在闭区间 上连续
• 在开区间 上可导

则存在 ，使得

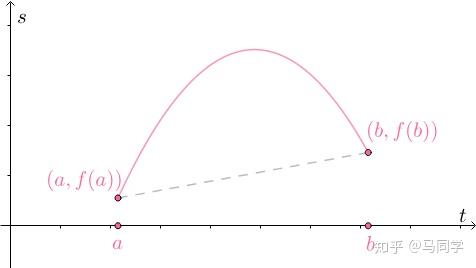
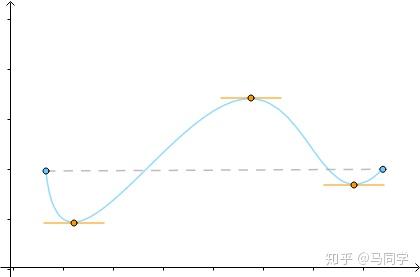
这个定理的几何意义就是，至少存在一点的切线与端点的连线平行；物理意义是，至少存在一点的速度与平均速度相等：

把它旋转一下，使得 ：

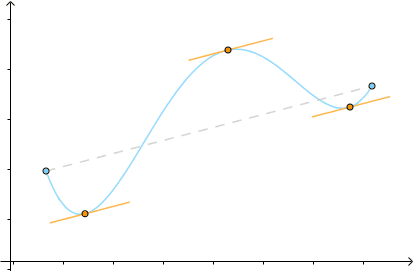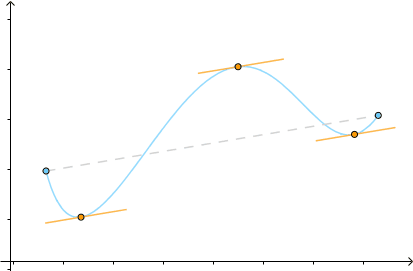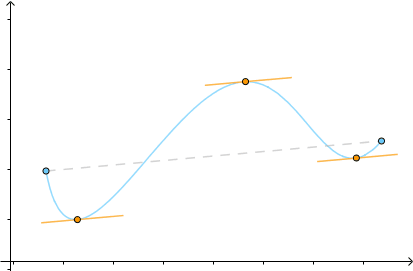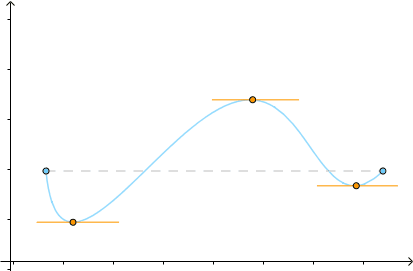
得到的就是罗尔中值定理，可见罗尔是拉格朗日的特例：

3 柯西中值定理

3.1 二维空间中的运动

之前讨论的是一维空间中的运动，下面来看看二维空间中的运动（关于这点，可以参看课程中“参数方程求导与相关变化率”这一节）。假设参数方程：

描述了一个二维空间中的运动：

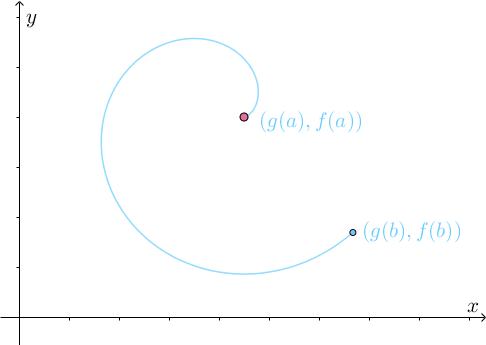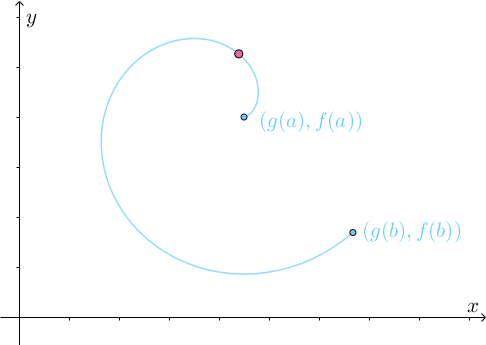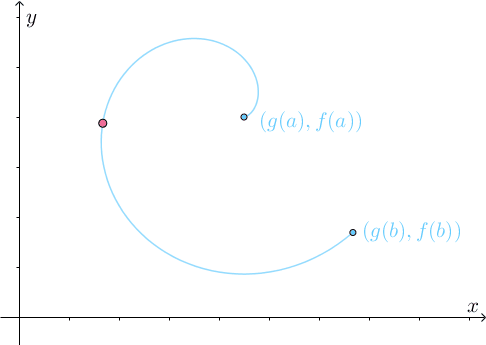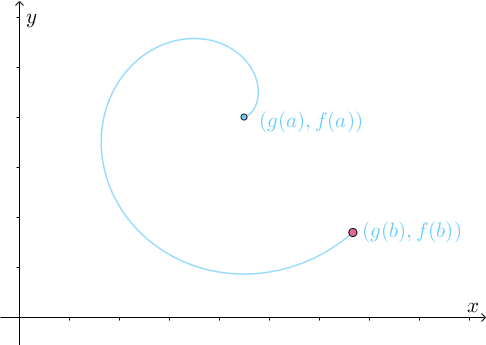
为了方便描述，令 、 ，那么上图描述的就是 时刻在 位置， 时刻运动到了 位置。向量 就表明了最终的运动方向：

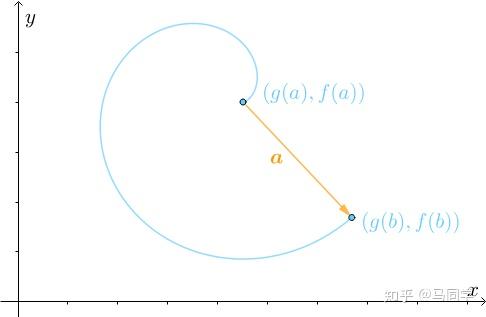
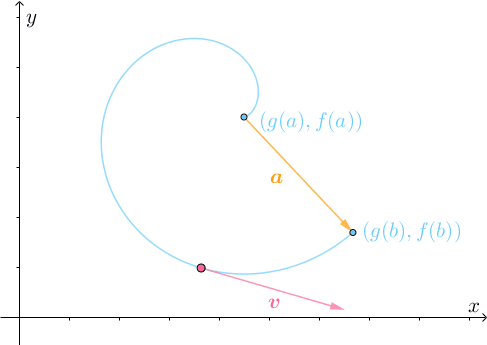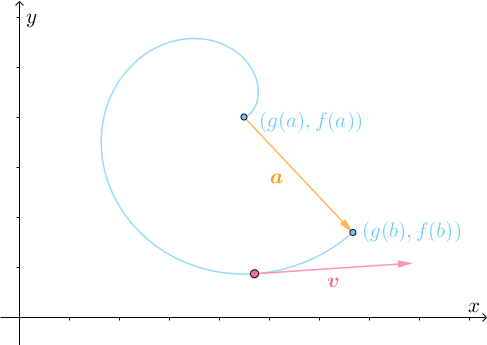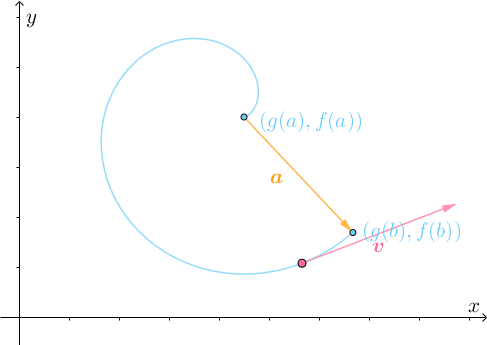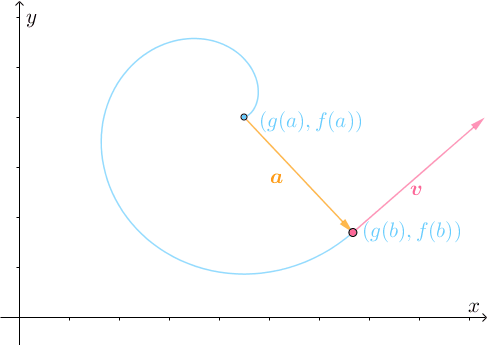
仔细分析此运动过程，刚开始的时候，速度 的方向与 相反，也就是说点是反着走的：

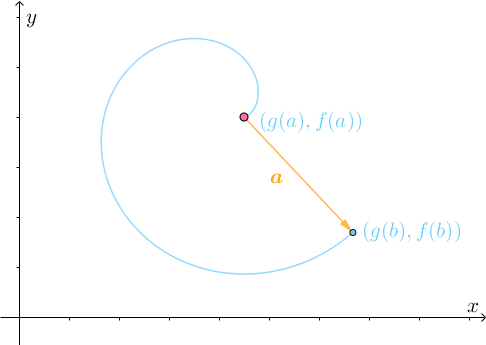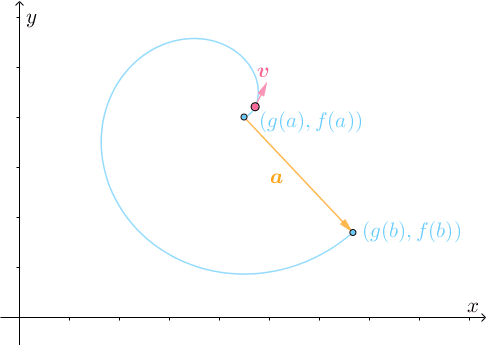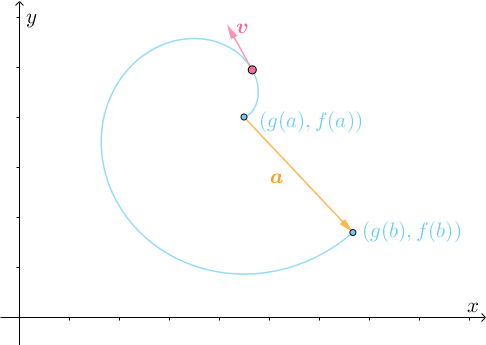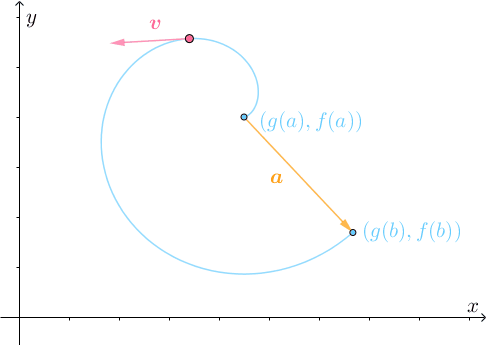
所以需要不断转弯调整：

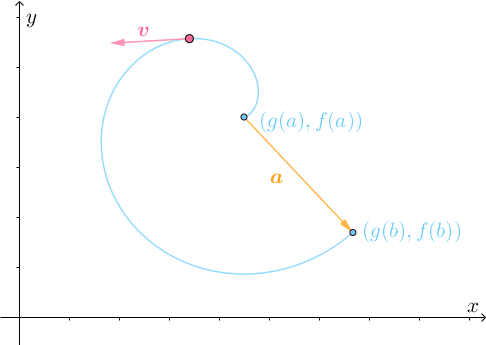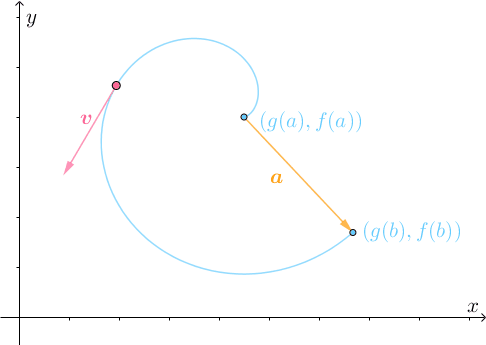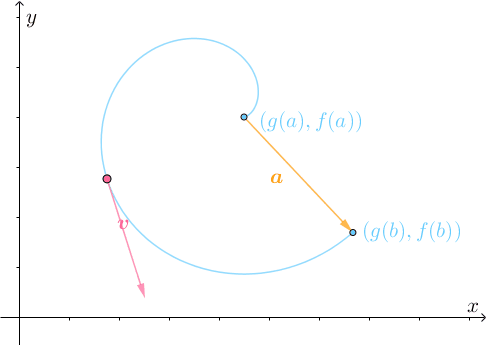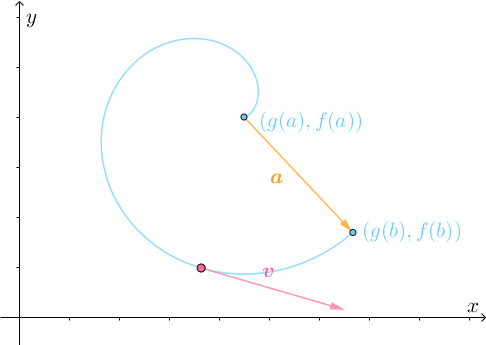
最终才能到达目的地：

容易想象，在转弯调整的过程中，必然会有 和 同向的时刻，比如 时刻：

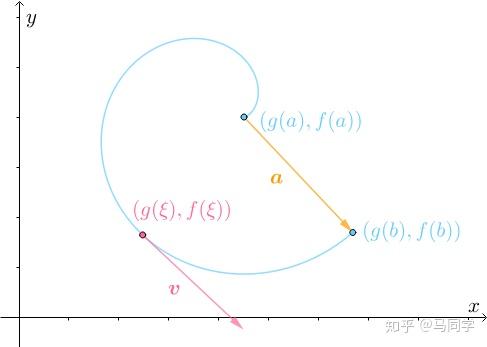
那么两者所在直线必然也平行：

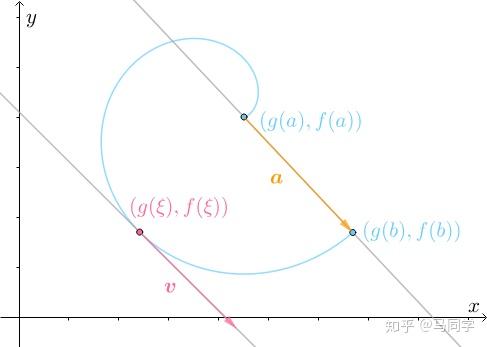
此时， 所在直线的斜率：

以及 所在直线的斜率（根据参数方程的求导法则）：

必然相等：

这就是柯西中值定理。

3.2 定理

设函数满足以下条件：

• 在闭区间 上连续
• 在开区间 上可导
• 有：

则存在 ，使等式

成立。

可以把 组合成参数方程：

这样柯西中值定理就有类似于拉格朗日中值定理一样的几何意义：

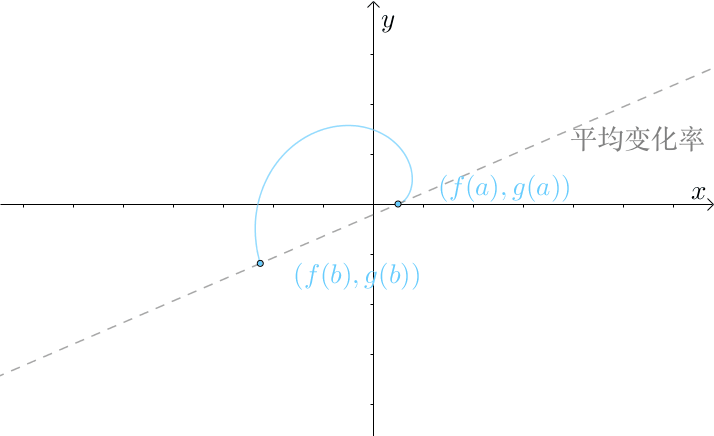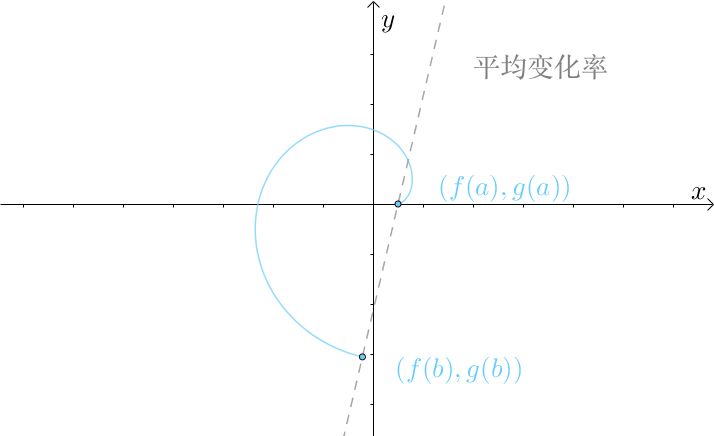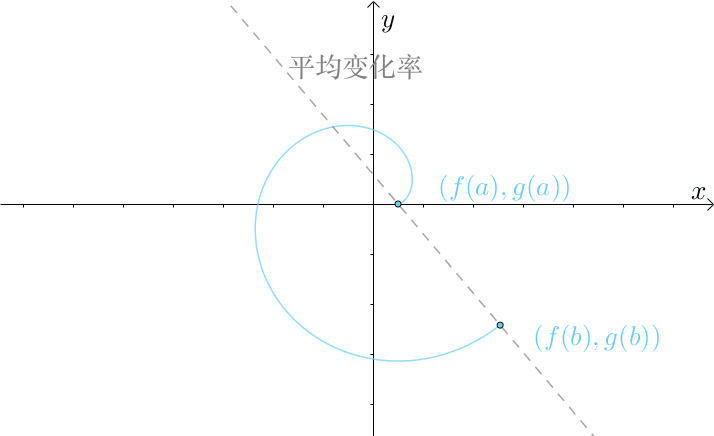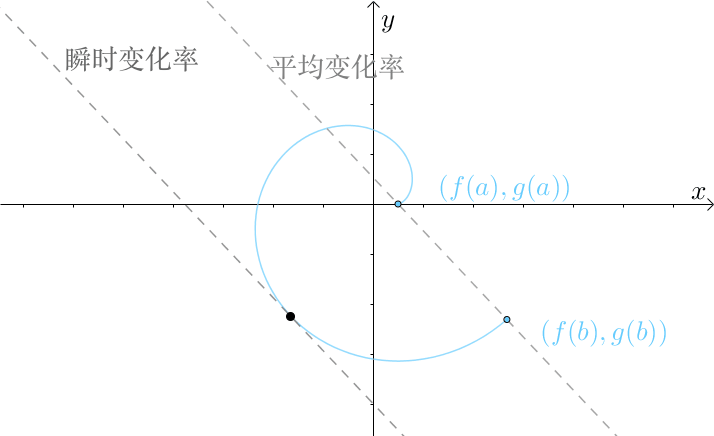
如果：

那么柯西中值定理就变为了拉格朗日中值定理，所以拉格朗日又是柯西的特例。

4 总结

三大微分中值定理的联系与区别：

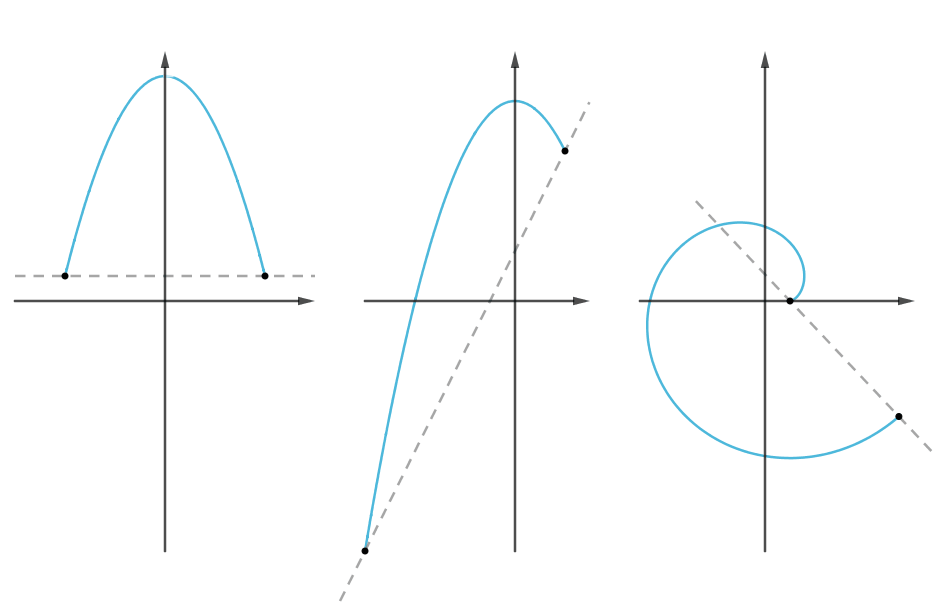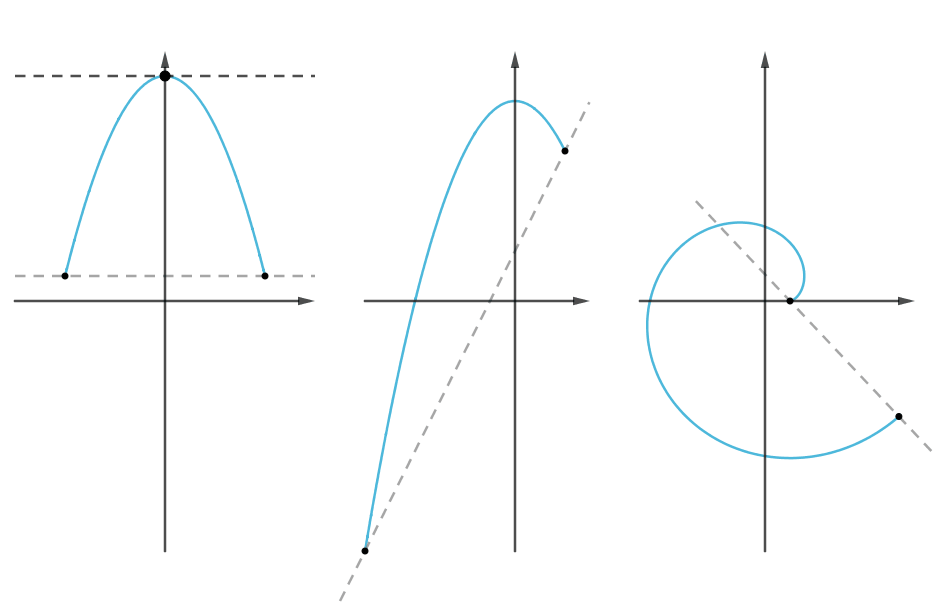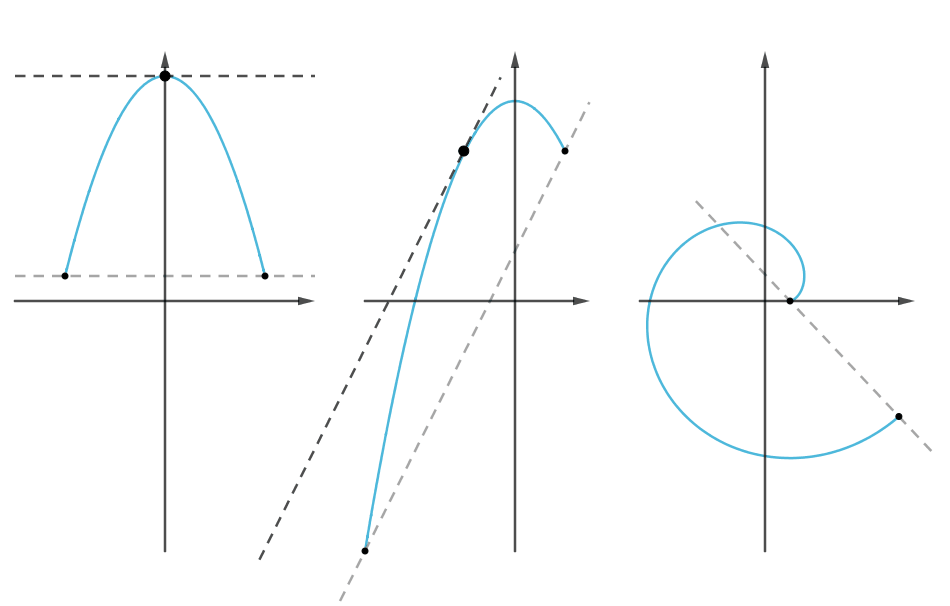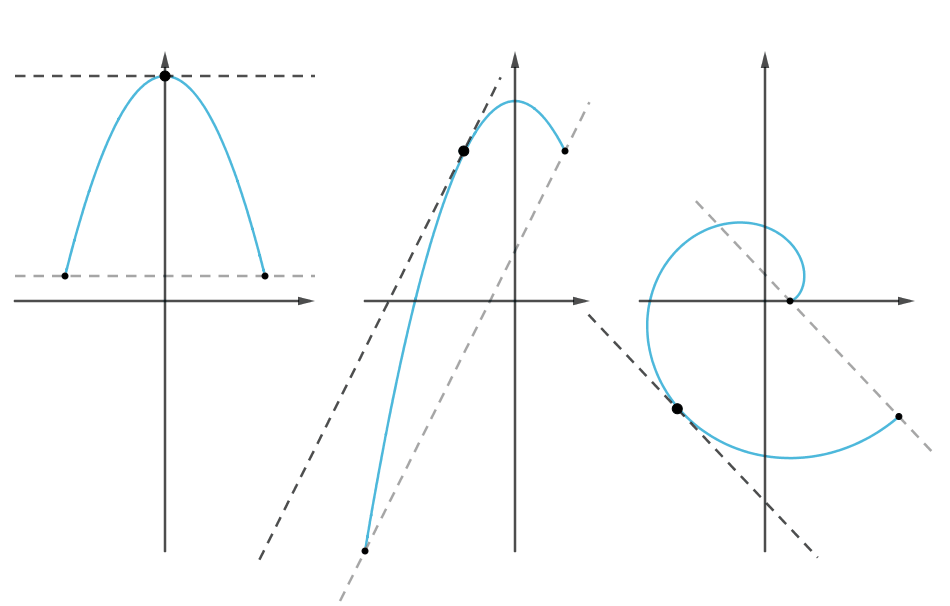
本文为微分中值定理的节选，因为格式问题，还有一些证明、扩展没有贴上来，可以到原文去查看。

蜡笔·小旧:
大神多发点线性代数的就好了，感觉秩啊，合同啊，之类的概念，特别需要用几何理解，可是又不会～ (95 赞)

　　
马同学 回复 蜡笔·小旧:
我们提供系统的线代付费课程，可以到公众号去看。 (6 赞)

　　
蜡笔·小旧 回复 马同学:
刚刚看了一下解锁的行列式部分，竟然里头没有柯西的几何定义，不像你文章的风格啊…… (4 赞)

　　
马同学 回复 蜡笔·小旧:
角度很多，后面有很多的几何解释 (1 赞)

　　
初学者 回复 蜡笔·小旧:
B站搜 3blue1brown (8 赞)

　　
蜡笔·小旧 回复 初学者:
感谢！

　　
GianT马 回复 初学者:
我就是3b1b里又一遍学了线代[赞同]

TGDLuck:
柯西中值定理写得太简略了。 (37 赞)

　　
马同学 回复 TGDLuck:
因为参数方程另文介绍了 (7 赞)

　　
东风锐气21 回复 TGDLuck:
[为难]就是两个拉格朗日中值定理的乘法形式
相除 (2 赞)

　　
徐天亚 回复 东风锐气21:
这个其实不是的 两个拉格朗日中值定理中 f导 和g导 不一定在同一个自变量处满足 只是形式上像 (5 赞)

　　
「已注销」 回复 东风锐气21:
你这个是错的，两个拉格朗日中值定理中取的点不能保证相同，相除以后导数相除式子中分母分子中的点根本就不不是一个 (4 赞)

　　
刘筱冲 回复 东风锐气21:
不对

　　
吴仲秋 回复 东风锐气21:
不对

PHOBIA:
拳击运动只要回到原点必有速度为0的时候 不太对，视频可以看出拳击是二维运动，比如绕圆匀速转动就是回到原点的，但速度不存在0点 (7 赞)

　　
马同学 回复 PHOBIA:
嗯，有点问题，应该用柯西来说明。 (2 赞)

　　
林同学 回复 PHOBIA:
是啊，拳击不太准确，改成击剑这种直线上的运动会更好。 (6 赞)

　　
Scot 回复 PHOBIA:
其实永拉格朗日中值定理也是能理解的，可以把匀速圆周运动看成一维直线上的简谐运动，是存在速度为0点的。或者把匀速圆周运动的位移-时间函数图像画出来，是一个正弦型函数，也存在速度为0。注意这里是速度不是速率

　　
PHOBIA 回复 Scot:
你说的是延某个轴速度为0...

吴道难:
1.3拓展是为了说明导数条件不需要那么严格对吧。建议修改一下，我一开始看还以为“闭区间可导”会让罗尔定理不成立。 (5 赞)

　　
马同学 回复 吴道难:
感谢指正

　　
Romer 回复 吴道难:
没有吧，高数书上就这么说的

王筝:
一般来说，如果我们问“能否把定理中的条件A换成条件B”，答案是不能的时候意味着在条件B下有反例。（隐含的是说条件B是比条件A弱的。）像罗尔定理里面的那一段，一般大家不会这么讲话的。 (6 赞)

　　
马同学 回复 王筝:
感谢指正 (1 赞)

雨断乌衣:
应该是开区间可导包含于闭区间可导吧，闭区间可导是要在开区间可导的基础上加上a右可导和b左可导。也就是说，闭区间可导的时候开区间一定可导，但开区间可导就没办法推出闭区间可导 (4 赞)

正义天使 凯尔:
刚学完就给我推荐这个？？？ (3 赞)

Johnny Shaw:
其实我更好奇为什么总有人不愿意翻书 (2 赞)

威士忌小哥哥:
大神们，我只想知道这些定理有什么用，怎么用，什么问题上用？ (1 赞)

　　
焰落火 回复 威士忌小哥哥:
知道这些就能灵活运用啦呀

王呼呼:
当年同济高数看的好痛苦，今天居然在你这里这么清晰的看懂了 (2 赞)

from: https://zhuanlan.zhihu.com/p/47436090