Wolfram长文全译:从简单规则到系统物理学(上)
title: Wolfram长文全译:从简单规则到系统物理学(上)
url: https://zhuanlan.zhihu.com/p/136150862
author: 集智科学家 (1b323571ffad3b1e289b0131572fbcf2)
column: 复杂性科学 (jake02)
voteup: 414 赞同
created: 2020-04-16 09:20:00
updated: 2020-04-16 09:20:00
fetched: 2022-05-08 16:53:20
count: 约 25419 字
version:
tags: [wolfram, 《一种新科学》(A-New-Kind-of-Science), 斯蒂芬·沃尔夫勒姆(Stephen-Wolfram)]
from 专栏 复杂性科学
话题:
wolfram, 《一种新科学》(A New Kind of Science), 斯蒂芬·沃尔夫勒姆(Stephen Wolfram)
正文:
导语
著名物理学家、《一种新科学》作者、Mathematica 设计师 Stephen Wolfram 于近日发表了近四万字的博文,在文中他详细的阐出了一套能够阐述宇宙基本物理理论的模型框架。集智俱乐部组织翻译了全文,以飨读者。
原文题目:
Finally We May Have a Path to the Fundamental Theory of Physics…
and It’s Beautiful
原文地址:
https://writings.stephenwolfram.com/2020/04/finally-we-may-have-a-path-to-the-fundamental-theory-of-physics-and-its-beautiful/
关于 Wolfram | Alpha 的集智百科:
https://wiki.swarma.org/index.php?title=斯蒂芬·沃尔夫勒姆_Stephen_Wolfram
目录
一.项目背景介绍(超图模型)
- I Never Expected This
- How It Works
- All Possible Rules
二.基本规则的搭建(维度、空间、时间)
- What Is Space?
- The Dimensionality of Space
- Curvature in Space & Einstein’s Equations
- Time
三.因果关系的表示
- The Graph of Causal Relationships
- The Importance of Causal Invariance
四.基本物理规律的推导(能量、质量、引力、宇宙学)
- Deriving Special Relativity
- What Is Energy? What Is Mass?
- General Relativity & Gravity
- Black Holes, Singularities, etc.
- Cosmology
- Elementary Particles—Old and New
- The Inevitability of Quantum Mechanics
五.基于图模型的系统物理学(统一时空、量子力学和相对论)
- General Relativity and Quantum Mechanics Are the Same Idea!
- Branchial Motion and the Entanglement Horizon
- Finding the Ultimate Rule
- Why This Universe? The Relativity of Rules
六.Wolfram 物理项目的前景
- The Challenge of Language Design for the Universe
- Let’s Go Find the Fundamental Theory!
一、 项目背景(超图模型)
梦想竟然实现了 I Never Expected This
对我来说,这实在是意想不到、令人难以置信的兴奋。是真的,在某种程度上我已经为此奋斗了近 50 年。但就在最近几个月,一切理论终于走到了一起。它比我想象的更美妙,更美丽。
在许多方面,这是自然科学的终极问题:我们的宇宙是如何运作的?有什么根本理论吗?在过去的几百年里,物理学领域已经有了惊人的发现。但是,即使已经做了所有这些事情——这非常令人印象深刻——我们仍然没有一个真正的物理学根本理论。
当我以研究理论物理为生的时候,我必须承认我并没有想太多去尝试找到一个根本的理论; 我更关心的是我们能够根据我们已有的理论得出什么结论。不知何故,我想我想象过,如果有一个根本理论,它将不可避免地变得非常复杂。
但是在 20 世纪 80 年代早期,当我开始研究简单程序的计算宇宙时,我有了一个非常令人惊讶和重要的发现:即使一个系统的基本规则非常简单,系统作为一个整体的行为本质上可以是任意丰富和复杂的。
这让我开始思考: 宇宙会这样运作吗?在我们所看到的物理学的丰富性和复杂性之下,是否存在着简单的规则呢? 我很快意识到,如果真是这样的话,我们实际上必须深入到时间和空间以及我们所知道的一切事物之下。我们的规则必须在一些较低的层次上运作,所有的物理学都必须浮现出来。
到 20 世纪 90 年代初,我对这些规则的运作有了明确的概念;到 20 世纪 90 年代末,我已经弄清楚了它们对于空间、时间、引力和物理学中其他事物的意义——基本上。并且我把它作为一个例子,在我的书《一种新科学》中用了将近 100 页的篇幅讨论这个问题。

空间:https://www.wolframscience.com/nks/p475--space-as-a-network/ 时间:https://www.wolframscience.com/nks/p486--time-and-causal-networks/ 引力:https://www.wolframscience.com/nks/p530--the-phenomenon-of-gravity/ 物理学:https://www.wolframscience.com/nks/chap-9--fundamental-physics/
我一直想要发起一个大项目,让我的想法更进一步。我试着从 2004 年开始。但是很快我就沉迷于创建 Wolfram | Alpha,以及 Wolfram 语言和它周围的一切。有时候我会见到我的物理学家朋友,我会谈论我的物理项目。他们会表现出礼貌的兴趣,但基本上他们的感觉是,找到一个物理学的根本理论太难了,而且只有疯子才会去尝试。
Wolfram | Alpha:https://www.wolframalpha.com/
我的想法中有些东西困扰着我,这对我没有任何帮助。我制定规则的方式似乎有点太死板,太做作。作为一个计算语言设计师,在我的的生活中,我一直在思考规则的抽象系统。偶尔我会想,它们是否与物理学有关。但我从来没有取得任何进展。直到2018 年秋天,我突然有了一个小小的想法
从某种程度上来说,它是简单而明显的,如果非常抽象的话。但是对我来说最重要的是它是如此的优雅和简约。终于,我有了一个对我来说是正确的东西,一个物理学如何工作的严肃的可能性。但是,Wolfram 语言的奇妙就在于此,我正忙着思考最终拥有一个全面的计算语言的所有意义。
但是,在 2019 年我们一年一度的暑期学校上,有两个年轻的物理学家(乔纳森 · 戈拉德和马克斯 · 皮斯库诺夫)说,“你必须追求这个! ” 在我年轻的时候,物理学一直是我最大的热情,在 2019 年 8 月,我过了一个盛大的生日,我意识到,是的,这么多年过去了,我真的应该看看我能不能做点什么。
因此,我和那两位曾经鼓励过我的年轻物理学家一起,从 2019 年 10 月开始认真工作。经过一辈子的研发,我们现在有了很好的计算工具。没过多久,我们就发现了一些我可以称之为“非常有趣的东西”。我们更优雅地复制了我在上世纪 90 年代所做的事情。从微小的、无结构的规则中,出现了空间、时间、相对论、引力和量子力学的暗示。
我们做了无数的计算机实验,对相关概念建立了直觉。渐渐地,事情变得越来越清楚。我们开始了解量子力学是如何工作的。然后我们意识到什么是能量。我们发现了我已故的朋友兼导师理查德 · 费曼的路径积分的一个大纲推导。我们开始看到相对论和量子力学之间的一些深层结构联系。一切都开始井井有条。所有这些我在物理学领域已经知道了近 50 年的事情——最终我们终于找到了一种方法,不仅可以知道什么是真的,还可以知道为什么。
我从没想过会发生这样的事。我原以为我们会开始探索简单的规则,如果幸运的话,我们会逐渐得到一些与物理学有关的线索。我想也许我们能够有一个宇宙最初几秒钟的可能模型,但是我们会花费数年时间试图看看它是否真的与我们今天看到的物理学相联系。
最后,如果我们要有一个完整的物理学基础理论,我们必须找到我们的宇宙的具体规则。我不知道这会有多难。我不知道这需要一个月,一年,十年还是一个世纪。几个月前我还会说,我甚至不知道我们是否有找到它的正确框架。
但我不会再这么说了,很多措施都有效。很多事情都已发生。我们不知道我们的规则是如何建立的具体细节是否正确,或者最终的规则是否简单。但是在这一点上,我确信我们所拥有的基本框架从根本上告诉了我们物理学是如何工作的。
对于科学模型来说,比较你投入了多少和得到了多少总是一种考验。我从来没有见过这么接近的东西。我们放进去的东西已经很小了。但是我们得到的是物理学中已知的最复杂的东西。最令我吃惊的是,至少到目前为止,我们还没有遇到过一件我们不得不说“哦,解释说我们必须在我们的模型中添加一些东西”的事情。有时候看到事物是如何运作的并不容易,但到目前为止,问题总是在于理解模型已经说了什么,而不是添加新的东西。
在最低层次上,我们已经得到的规则几乎是最低限度的(有趣的是,它们的基本结构可以用一行符号 Wolfram 语言代码的一小部分来表示)。在他们原始的形式中,他们并没有真正参与所有存在的丰富的思想和结构,例如,在数学中。但是一旦我们开始研究这些规则被无数次应用的后果,我们就会清楚地发现,这些规则与最近许多精彩的数学运算有着非常优雅的联系。
物理学也有类似的东西。我们的模型的基本结构看起来很奇怪,与至少在过去的一个世纪里物理学所做的几乎所有事情都完全不同。但是随着我们进一步研究我们的模型,惊人的事情发生了:我们发现不只是一个,而是许多在过去几十年中在物理学中追求的流行的理论框架实际上与我们的模型直接相关。
我担心这会成为“你必须扔掉旧的”科学进步之一。并非如此。是的,我们模型的基本结构是不同的。是的,最初的方法和方法是不同的。是的,我们需要一些新的想法。但是,为了让一切运转正常,我们必须建立在我的物理学家朋友们在过去几十年里一直努力工作的基础上。
然后还有物理实验。如果你几个月前问我,什么时候我们能从我们的模型中得到任何实验上可测试的东西,我会说它很遥远。在我们基本上找到最终规则之前,这种情况可能不会发生。但看起来我错了。事实上,我们已经得到了一些奇怪的新事物的线索,它们可能就在那里等着我们去寻找。
好的,那么我们现在需要做什么?我很激动地说,我认为我们已经找到了一条通往物理学根本理论的道路。我们已经建立了一个范例和框架(是的,我们也建立了许多好的、实用的、计算性的工具)。但是现在我们需要完成这项工作。我们需要解决许多复杂的计算、数学和物理问题。看看我们能否最终找到宇宙基本运作的答案。
这是一个激动人心的时刻,我想与大家分享。我期待着深入参与其中。但这不仅仅是我或者我们小团队的一个项目。这是一个面向全世界的项目。这将是一个伟大的成就,当它完成时。我希望看到它被尽可能广泛地分享。是的,许多必须做的事情都需要顶尖的物理和数学知识。但我想尽可能广泛地揭露一切,这样每个人都能参与进来ーー我希望能从我认为将是一次伟大的、具有历史意义的知识探险中得到启发。
今天我们正式启动我们的物理项目。从现在开始,我们将直播我们正在做的事情——与世界分享我们实时发现的任何东西(我们也将很快发布我们已经积累的 400 多小时的视频)。我发布了自上世纪 90 年代以来的所有工作资料,我们也发布了所有的软件工具。我们会发布有关进展的公告,还会有围绕这个项目的教育项目。
哦,是的,我们正在建立一个值得注意的宇宙的登记处(Registry of Notable Universes)。这里已经有将近一千条规则。我不认为那里面的任何一个都是我们自己的宇宙——尽管我不能完全确定。但是,我希望在不久的某个时候,在注册表中输入一条具有所有正确属性的规则,我们将慢慢地发现,是的,就是这条规则,我们的宇宙终于被解码了。

How It Works? 怎么做到的?
好吧,那么这一切是如何运作的呢?我写了一个 448 页的技术说明(是的,过去几个月我一直很忙)。我们团队的另一位成员(乔纳森 · 戈拉德)已经写了两篇 60 页的技术论文。在这个项目的网站上还可以找到其他材料。但是在这里,我将给出一个相当非技术性的总结,来概括其中的一些亮点。
技术展览会地址:https://www.wolframphysics.org/technical-introduction 技术论文地址:https://www.wolframphysics.org/technical-documents/ 项目网站地址:https://www.wolframphysics.org/
一切都始于非常简单和非常无结构的东西。 我们可以把它看作是抽象元素之间抽象关系的集合。或者我们可以把它想象成一个超图(hypergraph)——或者,在简单的情况下,一个简单图(graph)。
关于超图的集智百科:超图 Hypergraph - 集智百科
我们可能有一系列的关系,比如:{{1, 2}, {2, 3}, {3, 4}, {2, 4}},可以用图表来表示:
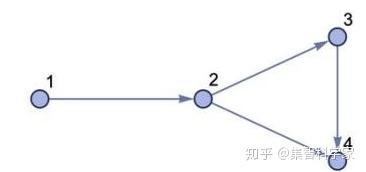
我们在这里指定的是元素之间的关系(比如{2,3})。我们陈述关系的顺序并不重要(尽管每个关系中的顺序也很重要)。当我们绘制图表时,最重要的是什么与什么相关; 页面上的实际布局只是为了视觉表现而做的选择。元素叫什么也不重要。在这里我使用了数字,但重要的是元素是不同的。
那么,我们如何处理这些关系(或图)的集合呢?我们只是一遍又一遍地对他们应用一个简单的映射规则。下面是一个可能的规则的例子: {{x, y}, {x, z}} → {{x, z}, {x, w}, {y, w}, {z, w}}
这个规则所说的是从集合中的任何地方获取两个关系,然后看看它们中的元素是否匹配左侧的模式{ x,y } ,{ x,z }(在 Wolfram 语言中是{ x,y } ,{ x,z }) ,其中两个 x 可以是任何元素,但两个 x 必须是相同的,y 和 z 可以是任何元素。如果有匹配,那么用右边的四个关系替换这两个关系。新出现的 w 代表一个新元素,唯一的要求是它必须与所有其他元素不同。
我们可以用图的变换来表示这个规则:
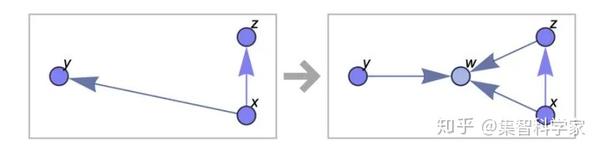
现在让我们将应用这个规则到图:{{1, 2}, {2, 3}, {3, 4}, {2, 4}}{2,3}和{2,4}关系匹配,
应用规则并让四个新关系替换它们,所以结果是:{{1, 2}, {3, 4}, {2, 4}, {2, 5}, {3, 5}, {4, 5}}
我们可以用一个图来表示这个结果 :
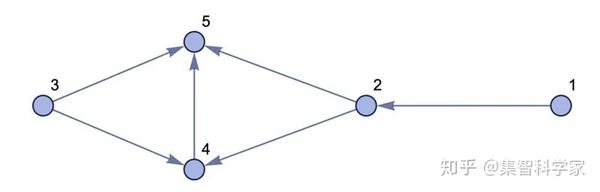
那么,如果我们一遍又一遍地应用这个规则会发生什么呢? 结果如下:
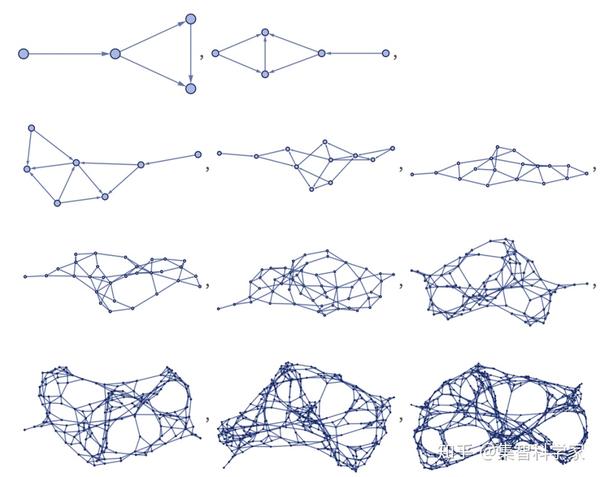
让我们再做几次,做一个更大的图:
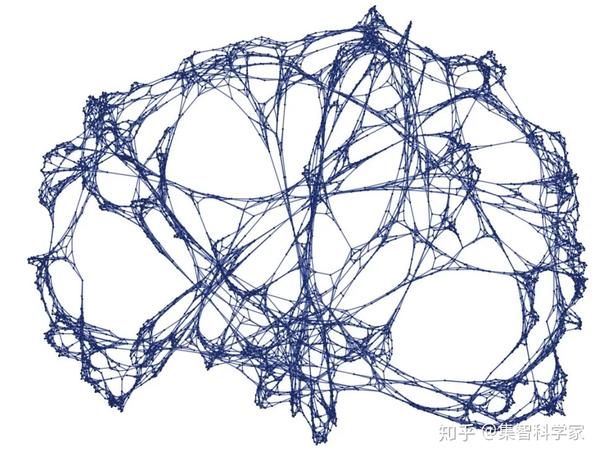
这里发生了什么?尽管我们有这样简单的一个规则。然而,一遍又一遍地应用这个规则,产生了一些看起来非常复杂的东西。这不是我们的直觉告诉我们应该发生的事情。但实际上—— 正如我在 20 世纪 80 年代初首次发现的那样——这种内在的、自然发生的复杂性在简单的规则和简单的程序中是无处不在的。比如我的书《一种新科学》就是关于这整个现象,以及为什么它对科学和其他领域如此重要。
但这里最重要的是,它将构成我们的宇宙,以及宇宙中的一切。让我们再回顾一下我们所看到的。我们从一个简单的规则开始,它告诉我们如何转换关系的集合。但是我们得到的是这个看起来很复杂的物体,在其他事物中,似乎有一些确定的形状。
我们设定任何形状,只是给出了一个简单的规则。并利用这个简单的规则绘制了图表。当我们想象这个图形时,它看起来就像是一个确定的形状。
如果我们忽略宇宙中的所有物质,我们的宇宙基本上就是一大块空间。但是那个空间是什么呢?两千年来,我们一直对它进行数学理想化和抽象化。但到底是什么呢?它是由什么东西组成的吗?如果是的话,是什么?
嗯,我认为它非常像上面的图。一大堆本质上抽象的点,抽象地连接在一起。除了图中有 6704 个这样的点,然而在我们真实的宇宙中可能有更多这样的点,甚至更多。
一切可能的规则 All Possible Rules
我们(目前)还不知道一个代表我们宇宙的实际规则——而且几乎可以肯定,它不是我们刚才谈论的那个规则。那么让我们来讨论一下有哪些可能的规则,以及它们通常会做些什么。
我们上面使用的规则的一个特性是它基于“二元关系”的集合,包含成对的元素(比如{2, 3})。但是同样的设置也让我们考虑与更多元素的关系。例如,下面是两个三元关系的集合:{{1, 2, 3}, {3, 4, 5}}
我们不能使用一个普通的图来表示这样的事情,但是我们可以使用一个超图。超图中一个边不再是连接两个节点,而可以是任意数量,也被称为“超边”。
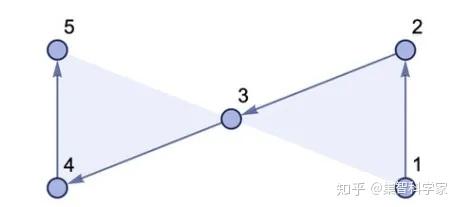
(注意,我们正在处理有向超图,其中节点在超边中出现的顺序很重要。在图中,“膜”只是表明哪些节点连接到同一个超边)
我们也可以为超图制定规则:{{x, y, z}} → {{w, w, y}, {w, x, z}}
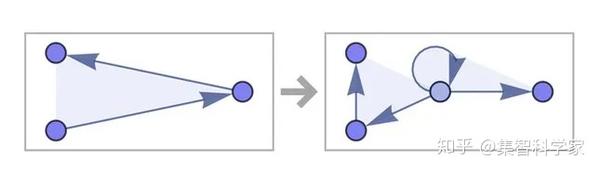
如果我们从最简单的三元超图-三元自循环{0, 0, 0}开始运行这个规则,结果会是这样的:
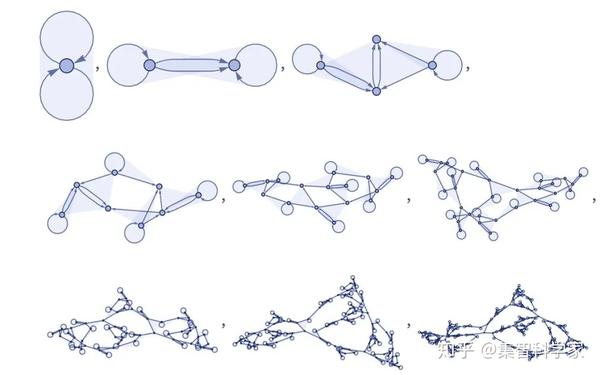
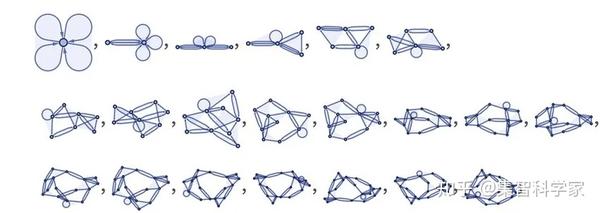
好,那么如果我们开始随机选择简单的规则会发生什么呢?以下是他们做的一些事情:
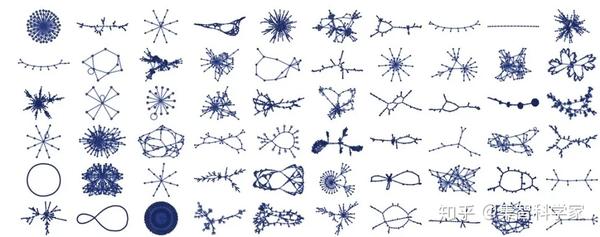
从某种程度上来说,这看起来非常具有动物学意义(而且,是的,这些模型肯定与基础物理学以外的其他事物有关——尤其是分子尺度的构造)。但基本上我们在这里看到的是,有各种各样的共同行为形式,有些很简单,有些则不然。
下面是我们看到的一些例子:

最大的问题是:如果我们运行这样的规则足够长的时间,它们最终会制造出复制我们物质宇宙的东西吗?或者,换句话说,在这个简单规则的计算宇宙中,我们能找到我们的物理宇宙吗?
然而,一个大问题是:我们怎么知道?我们在这里看到的是应用规则几千次的结果; 在我们实际的宇宙中,它们可能已经应用了10^500次,甚至更多次。要弥合这个差距并不容易。我们必须从两方面着手。首先,我们必须使用过去几个世纪我们在物理学中所学到的对宇宙运行的最好总结。其次,我们必须尽我们所能去弄清楚我们的规则到底是做什么的。
这里有一个潜在的基本问题: 计算不可约性(computational irreducibility) 。从三个世纪前开始,数学科学的伟大成就之一就是提供方程式和公式,这些方程式告诉你一个系统将如何运作,而不需要你追踪系统运作的每一个步骤。但是很多年前,我意识到在可能规则的计算宇宙中,这通常是不可能的。相反,即使您知道系统遵循的确切规则,您可能仍然无法计算出系统将做什么,除非跟踪它所需的每一个步骤。
有人可能会设想,一旦我们知道了某个系统的规则,那么我们所有的计算机和脑力总是能够“跳跃前进” ,并计算出该系统将做什么。但实际上,有一个我称之为计算等价原理的东西,意思是,几乎任何时候,一个系统的行为都不是明显的简单,它的计算复杂程度比任何东西都高。所以我们不能“超越”它——而计算出它的功能将需要巨大的计算工作量。
对于我们的宇宙模型来说,这可能是个大问题。因为我们不可能像宇宙一样长时间运行这些模型。从一开始,我们还不清楚是否能够从我们能做的事情中得出足够的结论,看看它是否符合物理学。
但最近让我感到惊讶的是,我们似乎很幸运。我们知道,无论何时,系统中存在计算不可约性,同时也存在无限多的计算可约性。但是完全不清楚在我们的案例中,这些口袋是否与我们从物理学中知道的东西一致。令人惊讶的是,似乎他们中的很多人都这么做了。
二、 基本规则的搭建(维度、空间、时间)
什么是空间?What Is Space?
让我们来看看无限集合中的一个特定的简单规则:{{x, y, y}, {z, x, u}} → {{y, v, y}, {y, z, v}, {u, v, v}}
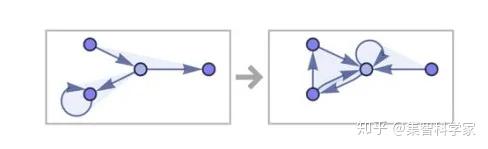
它可以这样运作:
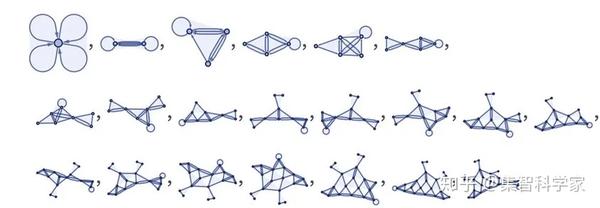
过了一段时间,就会发生这样的情况:
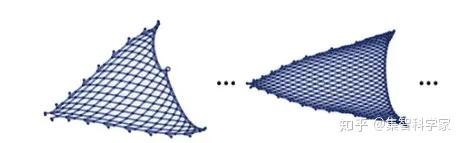
它基本上让我们成为一个非常简单的“空间碎片”。如果我们继续做下去,时间越来越长,网格就会变得越来越精细,以至于我们几乎无法分辨出它是连续平面的一部分。
这里有一个不同的规则:{{x, x, y}, {z, u, x}} → {{u, u, z}, {v, u, v}, {v, y, x}}
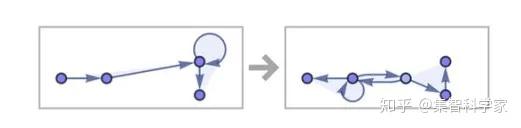
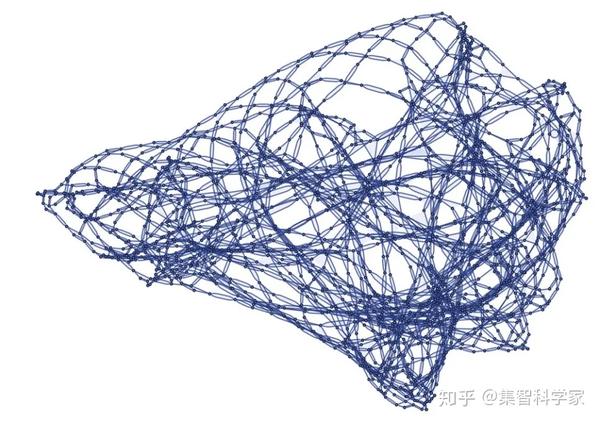
它看起来像是在“试图创造” 3D 的东西。这里还有另外一条规则:{{x, y, z}, {u, y, v}} → {{w, z, x}, {z, w, u}, {x, y, w}}
这不是很奇怪吗?我们的规则,只是说明如何重写一个抽象的超图,没有几何概念或任何与 3维空间有关的事情。然而,它产生了一个超图,这个超图看起来想个三维曲面。
即使这里唯一真正的东西是点之间的连接,我们可以“猜测”曲面可能在哪里,然后我们可以在 3D 中显示结果:

如果我们继续下去,就像平面的例子一样,网格会变得越来越细,直到这些基本规则把格点一点一点地生长并接连接成像你可能在微积分课上学习的那种连续的3D曲面。当然,在某种意义上,它并不是“真的”那个曲面:它只是一个超图,代表了一系列抽象关系——但不知何故,这些关系的模式赋予了它一个越来越接近曲面的结构。
这基本上就是我认为宇宙中的空间是如何运作的。实际上,它是一堆离散的,抽象的点之间的关系。但是在我们正在经历的范围内,它的关系模式使它看起来像我们习惯的那种连续的空间。这有点像水,下面是一堆分立的分子。但对我们来说,它看起来像是一种连续的流体。
不用说,自古以来,人们就认为空间可能本质上是离散的。但是在现代物理学中,从来没有一种理论来说明这一点——因为可以用微积分,连续性太方便了。但是现在看来,对于理解物理学的基本理论,空间是离散这一理念非常重要。
空间的维度 The Dimensionality of Space
关于我们所经历的空间,一个非常基本的事实是,它是三维的。那么我们的规则能重现这一点吗?我们刚刚看到的两个规则产生了我们可以很容易识别的二维曲面——一种是平面的,另一种是以某种形状排列的。当然,这些都是(二维)空间的简单例子:它们实际上只是简单的网格。虽然这使得它们很容易被识别,但这也意味着它们实际上不太像我们的宇宙,在某种意义上,它们还有更多的内容。
那么好吧,举个例子:

如果我们继续下去足够长的时间,这是否会形成类似空间的东西,如果是的话,有多少维度?要知道答案,我们必须有一些鲁棒的方法来度量维度。但是请记住,我们正在绘制的图只是可视化; 底层结构是定义超图的一堆离散关系——没有关于坐标、几何甚至拓扑的信息。顺便说一下,为了强调这一点,这里有一个完全相同的连接结构的同样的图表,以四种不同的方式呈现:
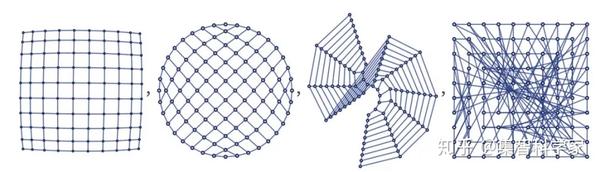
但是回到维度的问题,回想一下圆的面积是 πr²,球的体积是 4/3πr³。一般来说,d 维球体的“体积”是一个常数乘以 r^d,但现在想想我们的超图。从超图中的某一点开始。然后用所有可能的方法遵循 r 超边。在超图中,您有效地模拟了“球形球”。下面是对应于二维和三维格子的图的例子:


如果你现在计算通过“图形距离 r”(即通过图形中的 r 连接)达到的点数,你会发现在这两种情况下,它们确实像 r² 和 r³ 一样增长。
这给了我们一种方法来度量超图的有效维数。从一个特定的点开始,看看通过 r 步你能达到多少点:

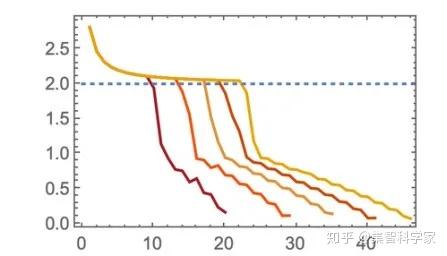
现在,要计算出有效维数,我们原则上只需要将结果与 r^d 相匹配。不过,这有点复杂,因为我们需要避免小 r(超图的每个细节都很重要)和大 r (超图的边缘),我们还需要考虑随着底层系统的演化,我们的“空间”是如何精化的。但是最终我们可以为有效维度生成一系列拟合,在这种情况下,这些拟合表明有效维度约为 2.7:
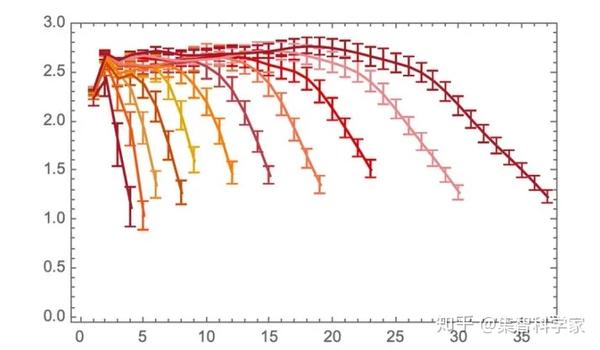
如果我们做同样的事情:
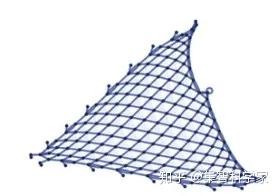
它局限于二维空间,它应该是这样的:
分数维数是什么意思?好吧,考虑一下分形,我们的规则可以很容易地做出来:{{x, y, z}} → {{x, u, w}, {y, v, u}, {z, w, v}}
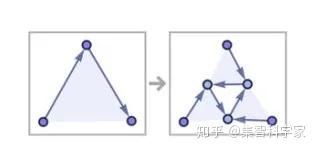
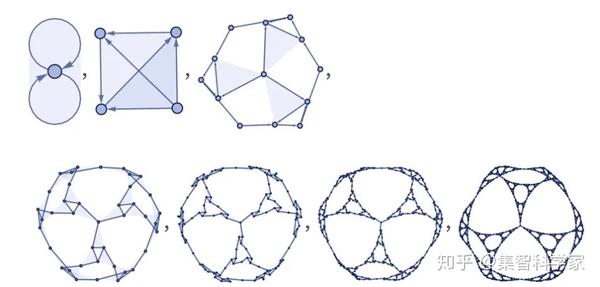
如果我们在这里测量维度,我们会得到 1.58—— Sierpiński 结构通常的分形维度:
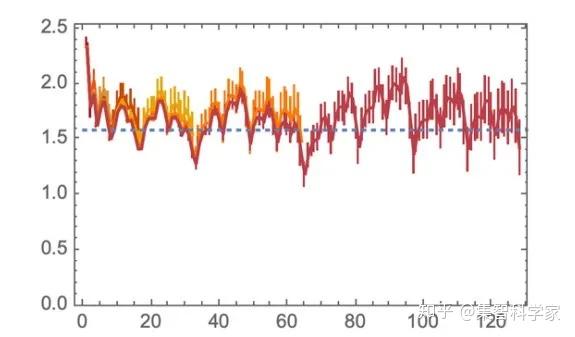
我们上面的规则并没有创建一个像这样规则的结构。事实上,即使规则本身是完全确定的,它使结构看起来相当随机。但是我们的测量结果表明,当我们继续运行这个规则时,它会产生类似于 2.7 维空间的东西。
当然了,2.7 不是 3,而且可以推测,这个特定的规则并不适用于我们的宇宙(如果我们迭代 10^100 次,它会有多少有效维度尚不清楚)。但是,测量维度的过程展示了一个例子,说明我们可以开始对规则的行为做出“物理可连接”的陈述。
顺便说一下,我们一直在谈论与我们的模型“创造空间”。但实际上,我们不仅仅是试图创造空间; 我们试图创造宇宙中的一切。在当前的标准物理学中,有一种空间(在数学上被描述为多面体)作为背景,然后是空间中的一切,所有的物质、粒子和行星等等。
但是,我们的模型中除了空间什么都没有——在某种意义上,宇宙中的一切都必须是“由空间构成”的。或者,换句话说,正是这个超图给我们提供了空间的结构,以及空间中存在的一切。
所以这意味着,例如,一个像电子或光子的粒子必须对应于超图的某些局部特征,有点像这个玩具的例子:
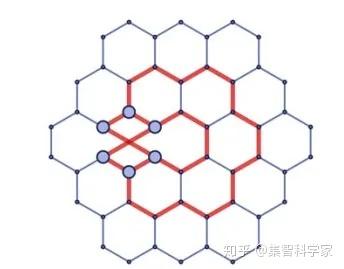
不过在尺度上,我的估计表明在代表我们宇宙这个超图的图中,“维持空间结构本身”的“活动”是维持我们已知存在于宇宙中的所有物质的活动的 10^200 倍。
空间曲率与爱因斯坦方程式 Curvature in Space & Einstein’s Equations
这里有一些简单的例子来说明我们的规则:
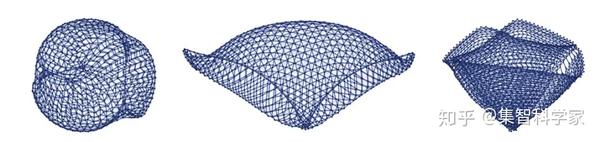
虽然所有这些看起来都像曲面,但它们显然是不同的。描述它们的一种方法是通过它们的局部曲率。事实证明,在我们的模型中,曲率是一个与维度密切相关的概念——这个事实对于理解重力是如何产生的,实际上是至关重要的。
但是现在,让我们来讨论一下如何在超图上度量曲率。通常圆的面积是 r²。但是让我们想象一下,我们在一个球体的表面画了一个圆,现在我们测量这个圆里面球体的面积:
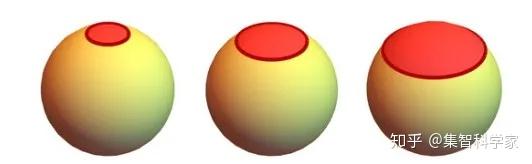
这个区域不再是 πr² 了。取而代之的是
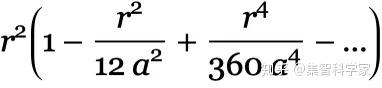
,其中 a 是球的半径。换句话说,随着圆的半径越来越大,在球体上的作用就越来越重要。(在地球表面,想象一下在北极周围画一个圆;一旦到达赤道,它就再也不会变得更大了)
如果我们将其推广到 d 维,就会得到体积增长率的公式
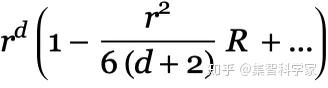
其中 R 是一个被称为 Ricci 标量曲率的数学对象。
所以这一切意味着,如果我们观察超图中球形球的增长率,我们可以期待两个贡献:一个对应于有效维数的 r^d 的主导项,和一个代表曲率的“修正项”r^(d+2)。
这里有一个例子,是关于一个有正曲率的二维空间:
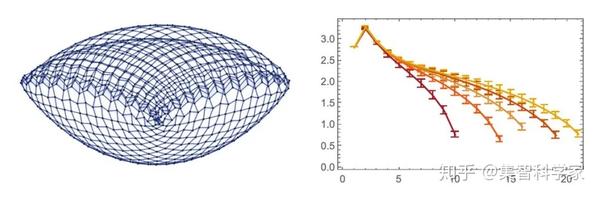
这里曲率的意义是什么?一是它表示测地线。测地线是两点之间最短的距离。在一般的平面空间中,测地线只是直线。但是当曲率存在时,测地线是弯曲的:
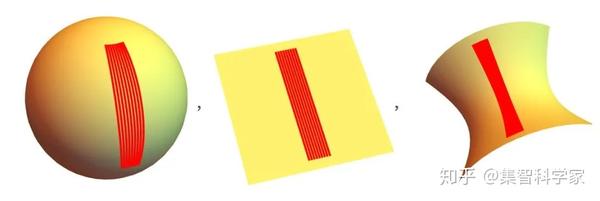
在正曲率的情况下,测地线束发散;在负曲率的情况下它们收束。但是,即使测地线最初被定义为连续空间(顾名思义,就是地球表面的路径),人们也可以把它们放在图(和超图)中。同样的道理:测地线是图(或超图)中两点之间的最短路径。
下面是根据我们的一个规则创建的“正曲率曲面”上的测地线:
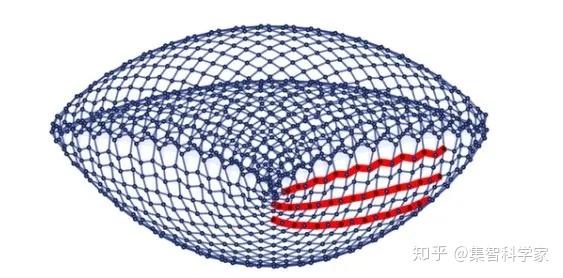
是一个更复杂的结构:
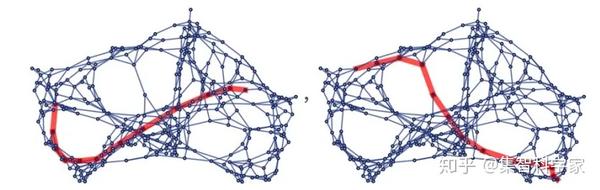
为什么测地线很重要?其中一个原因是,在爱因斯坦的广义相对论中,它们是光(或者自由落体中的物体)在空间中遵循的路径。在这个理论中,引力与空间的曲率有关。所以当有东西绕着太阳偏转时,这是因为太阳周围的空间是弯曲的,所以物体沿着的测地线也是弯曲的。
广义相对论对空间曲率的描述都是基于我们上面遇到的 Ricci 标量曲率 R(以及稍微复杂一点的 Ricci 张量)。但是,如果我们想知道我们的模型是否再现了爱因斯坦的引力方程,我们必须知道,从我们的超图中产生的 Ricci 曲率是否与理论模型相同。
这涉及到相当多的数学复杂性(例如,我们必须考虑空间 + 时间的曲率,而不仅仅是空间),最终在各种限制和各种假设下,我们的模型确实重现了爱因斯坦方程。(起初,我们只是重现了真空爱因斯坦方程,而没有涉及物质;当我们讨论物质,我们会看到,我们实际上得到了完整的爱因斯坦方程)
数学复杂性:https://www.wolframcloud.com/obj/wolframphysics/Documents/some-relativistic-and-gravitational-properties-of-the-wolfram-model.pdf完整的爱因斯坦方程:https://www.wolframphysics.org/technical-introduction/potential-relation-to-physics/matter-energy-and-gravitation
重现爱因斯坦方程是件大事。通常在物理学中,爱因斯坦方程是你开始的地方,而在这里,它们是由模型自发产生的。
关于怎么推导,我们有必要说一下。这实际上有点类似于,从许多离散分子的底层动力学极限推导出流体流动方程。但在这种情况下,我们计算的是空间的结构,而不是流体的速度。它包含了一些相同类型的数学近似和假设。例如,我们必须假设,系统中产生的有效随机性足以使统计平均值起作用。还有一大堆微妙的数学极限需要考虑。与单个超图的连接相比,距离必须很大,但与超图的整体大小相比,距离必须很小。
对于物理学家来说,“辨析”数学模型上的细微差别是相当常见的。其实这件事已经干了一个多世纪了,从分子动力学推导出流体方程。我们在这里也犯了同样的错误。在某种意义上,这是另一种说法,有很多精妙的数学要做,在实际上使得推导严谨,和准确理解它将在什么时候应用,等等。
顺便说一下,当涉及到数学,即使是我们已经有的设置是有趣的。微积分是建立在普通连续空间(局部逼近欧氏空间的流形)上的。但是我们这里有一些不同的东西:在一个无限大超图的极限中,它就像一个连续的空间,但是普通的微积分不适用于它(尤其是因为它不一定是整数维的)。所以为了更好地讨论它,我们必须发明一些对微积分的抽象,比如能够处理分数维空间中的曲率(也许目前最接近这个问题的数学是来自于非常活跃的几何群论领域)。
顺便说一句,值得注意的是,在改变空间的维度和有曲率之间的精确权衡中有很多微妙之处。虽然我们认为我们的宇宙是三维的,但根据我们的模型,至少存在局部偏差的可能——而且最有可能的是,在早期的宇宙中实际上存在大的偏差。
时间 Time
在我们的模型中,空间是由表示抽象关系集合的超图的大尺度结构定义的。但时间又是什么呢?
在过去的一个多世纪里,基础物理学普遍认为时间在某种意义上“就像空间”——例如,人们应该把空间和时间混为一谈,谈论“时空连续体”。当然,相对论也指向这个方向。但是如果说在过去的一个世纪里,物理学的历史上出现了一个“错误的转折” ,我认为那就是假设空间和时间是同一种东西。而在我们的模型中,这一点并不存在——即使如我们将看到的,相对论也得到了很好的证明。
那么时间是什么呢?实际上,它和我们体验到的差不多:事情发生和导致其他事情的不可阻挡的过程。但是在我们的模型中,它更加精确:它是规则的渐进式应用,不断地修改定义宇宙内容的抽象结构。
在我们的模型中,时间的版本在某种意义上是非常计算化的。随着时间的推移,我们实际上看到了计算中越来越多步骤的结果。的确,计算不可约性的现象意味着,有一些确定的和不可约的“实现”的过程(例如,我认为这种不可还原性,就是与熵增定律和热力学时间箭头相关的初始条件的“加密”的原因)。当然,不用说,我们的现代计算范式在一个世纪前引入“时空”时并不存在,如果存在的话,物理学的历史可能会有很大的不同。
但是,在我们的模型中,时间只是规则的渐进应用。但是在这个过程中有一个微妙之处,乍一看似乎是一个细节,但实际上却是巨大的,事实上是相对论和量子力学的关键。
在这篇文章的开头,我谈到了规则:{{x, y}, {x, z}} → {{x, z}, {x, w}, {y, w}, {z, w}}
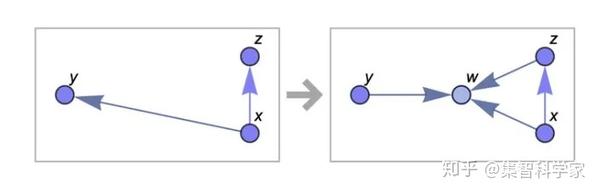
展示了应用它的“前几个步骤”
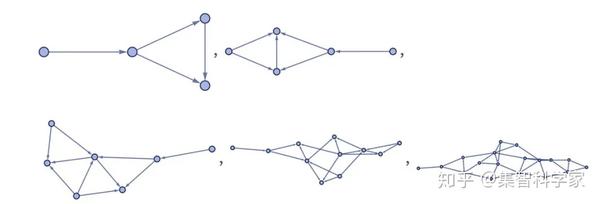
但是这个规则到底是如何被应用的呢?这些步骤的“内部”是什么?该规则定义了如何在超图中获取两个连接(在本例中实际上只是一个图)并将它们转换为四个新连接,从而在流程中创建一个新元素。因此,我们之前展示的每个“步骤”实际上都由几个单独的“更新事件”组成(这里突出显示了新添加的连接,而即将删除的连接则消失了) ):
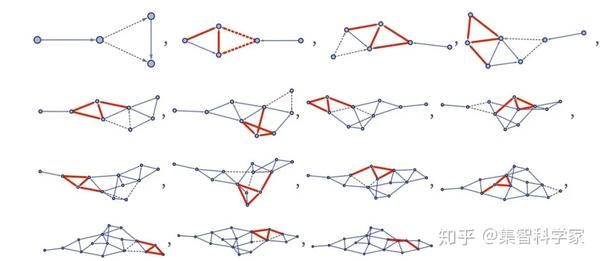
但是现在,关键的一点是:这不是唯一符合规则的更新事件序列。这个规则只是说找到两个相邻的连接,如果有几个可能的选择,它没有说明是哪一个。在我们的模型中,一个关键的想法就是在某种意义上把它们都做完。
我们可以用一个图表来表示,它显示了所有可能的路径:
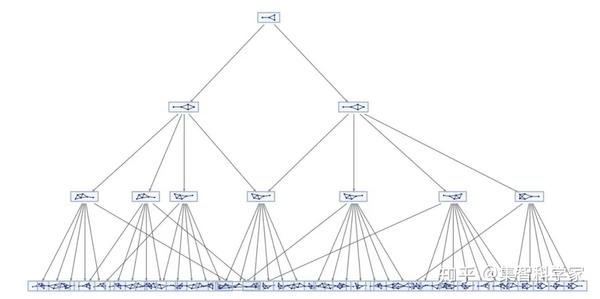
对于第一次更新,有两种可能性。对于这些结果中的每一个,都有四种额外的可能性。但是在下一次更新时,一些重要的事情发生了:两个分支合并了。换句话说,即使我们做了一系列不同的更新,结果也是一样的。
事情很快变得复杂起来。下面是更新后的图表,现在不再试图显示页面的进度:
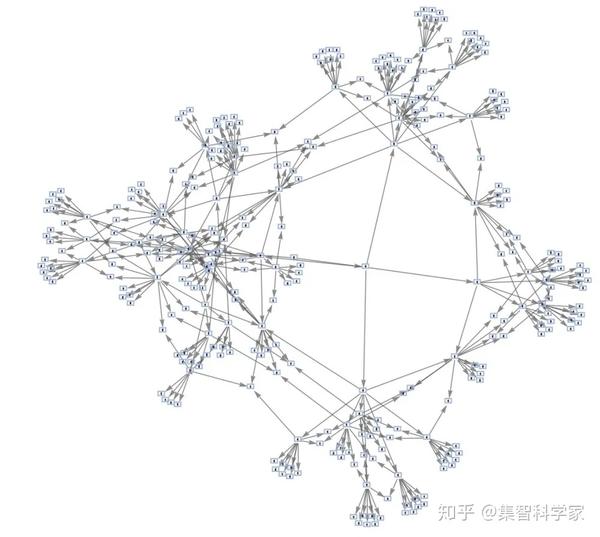
那么这和时间有什么关系呢?它所说的是,在模型的基本陈述中,不仅仅有一条时间路径,还有许多路径和“历史”。但是,这种模式——以及所使用的规则——决定了所有这些因素。我们还看到了一些其他的暗示: 即使我们可能认为我们正在沿着一条“独立”的历史道路前进,但它实际上可能与另一条道路合并。
我们需要多费些篇幅来解释这一切运作的原因。但现在我要说的是,将会出现的是时间与事物之间的因果关系,事实上, 即使所遵循的历史轨迹不同,这些因果关系最终可能是相同的——实际上,对于嵌入系统中的观察者来说,仍然只有一条时间线。
三、 因果关系的表示
因果关系图 The Graph of Causal Relationships
最终结果非常优雅。但是为了达到我们能够理解的优雅的宏观大局,我们需要通过一些细节(一个不可避免地建立在非常抽象概念基础上的物理学基本理论,其解释起来有些复杂,这并不十分令人惊讶,但事实就是如此)。
为了保持事情相对简单,我不打算直接谈论在超图上运行的规则。取而代之的是,我将要讨论的规则是在字符串上运行的(澄清一下:这些不是弦理论的组成部分——尽管在“双关成为科学”这个怪异的转折中,我怀疑我所讨论的字符串运算的连续限制实际上与现代物理学意义上的弦理论有关)。
假设我们有这样一条规则:{A → BBB, BB → A}
这条规则说,任何我们看到 A 的地方,我们可以用 BBB 替换它,任何我们看到 BB 的地方,我们可以用 A 替换它。因此,现在我们可以为这个规则生成所谓的多路系统,并绘制一个“多路图” ,显示可能发生的一切:
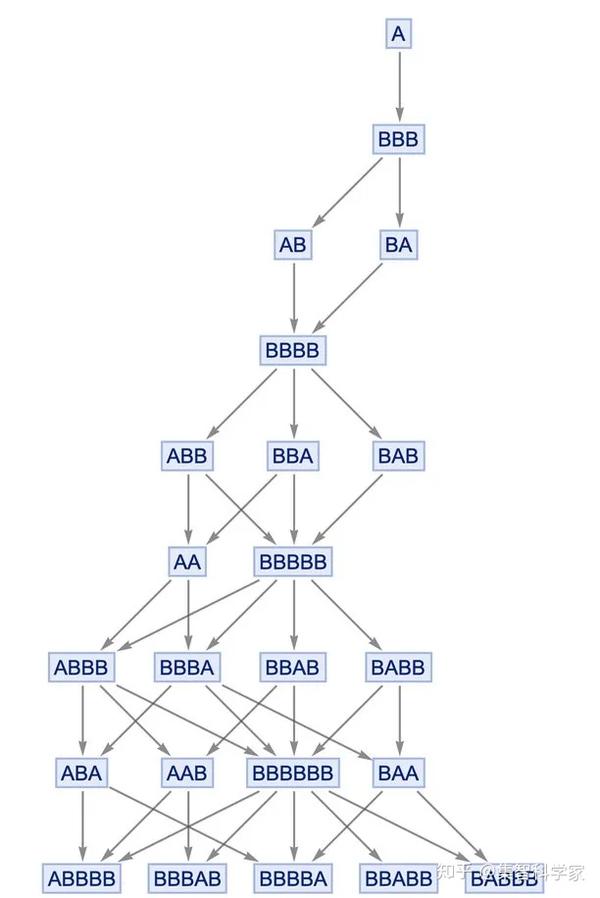
在第一步,唯一的可能性是使用 A → BBB, 用 BBB 替换 A。但是有两种可能性:第一个 BB 或者第二个 BB——这两种选择会产生不同的结果。然而,下一步,可以做的只能是更换 A——在这两种情况下都会得到 BBBB。
所以换句话说,即使我们在某种意义上有两条历史道路,在多元系统中分开,它们只需要一个步骤就会重新融合。如果你跟踪上面的图,你会发现这条规则总是这样:生成的每一对分支总是合并,在这种情况下,只需要多走一步。
分支和合并之间的这种平衡是一种我称之为“因果不变性”的现象。虽然这看起来像是一个细节,但事实证明,这就是为什么相对论成立的核心,为什么在量子力学中存在一个有意义的客观现实,以及基础物理学的许多其他核心特征。
但是让我们来解释一下为什么我称这个性质为因果不变性。上面的图只是显示了什么“状态”(即什么字符串)导致了什么另一个。但是,我们可以通过包含导致状态之间每次转换的更新事件来对多路图进行注释,这样可能会使图像变得更加复杂(并且要注意,与完整的超图相比,这是难以置信的简单):
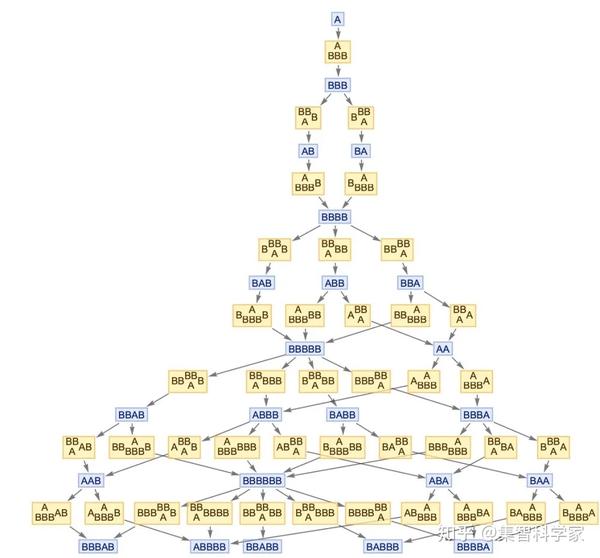
但是现在我们可以问这样一个问题:这些事件之间的因果关系是什么?换句话说,什么事件需要在其他事件发生之前发生?或者,换句话说,为了创建其他事件所需的输入,必须发生什么事件?
让我们更进一步,通过显示事件之间的所有因果依赖关系来注释上面的图表:
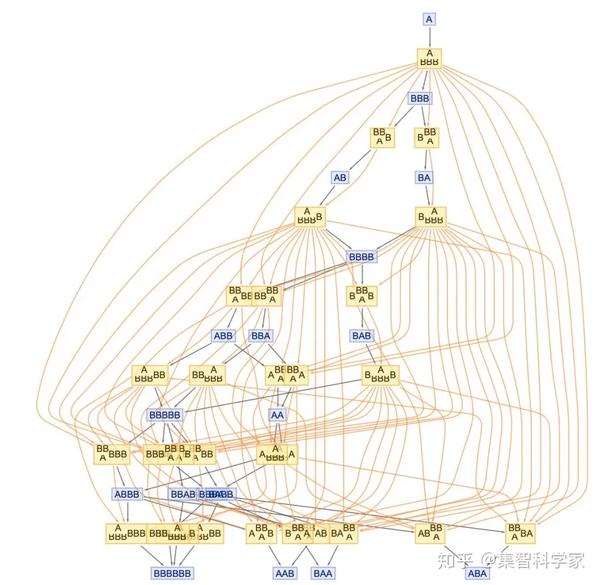
橙色线实际上表明了哪个事件必须先于哪个其他事件发生,或者多路系统中所有的因果关系是什么。是的,这很复杂。但请注意,这张图显示了整个多路系统——包括所有可能的历史路径——以及这些路径内部和之间的整个因果关系网络。
但是关于因果不变性有一个关键的问题: 它意味着,不管历史沿着哪条路走,因果关系图实际上是相同的。 这就是为什么我最初称这个性质为“因果不变性”——因为它说,对于这样一个规则,因果性质对于执行更新的序列的不同选择是不变的。
如果你通过上面的图进行追踪(再走几步),你会发现,对于历史的每一条路径,表示事件之间因果关系的因果图总是:
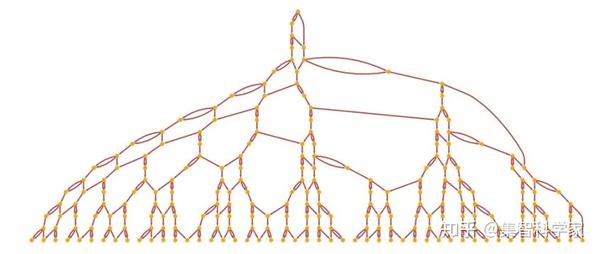
或者画得不一样一些,
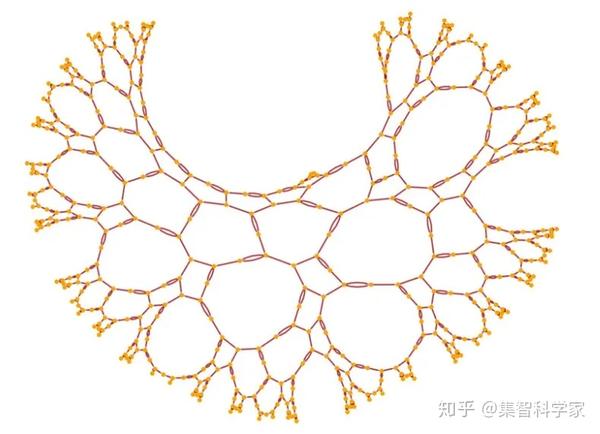
因果不变性的重要性 The Importance of Causal Invariance
为了更好地理解因果不变性,我们来看一个更简单的例子:规则 BA → AB 的情况。这条规则规定,任何时候一个字符串中有一个 B 后面跟着一个 A,交换这些字符。换句话说,这是一个试图将一个字符串分类为字母顺序的规则,一次两个字符。让我们从 BBBAAA 开始。下面的多向图显示了所有可能发生的事情:
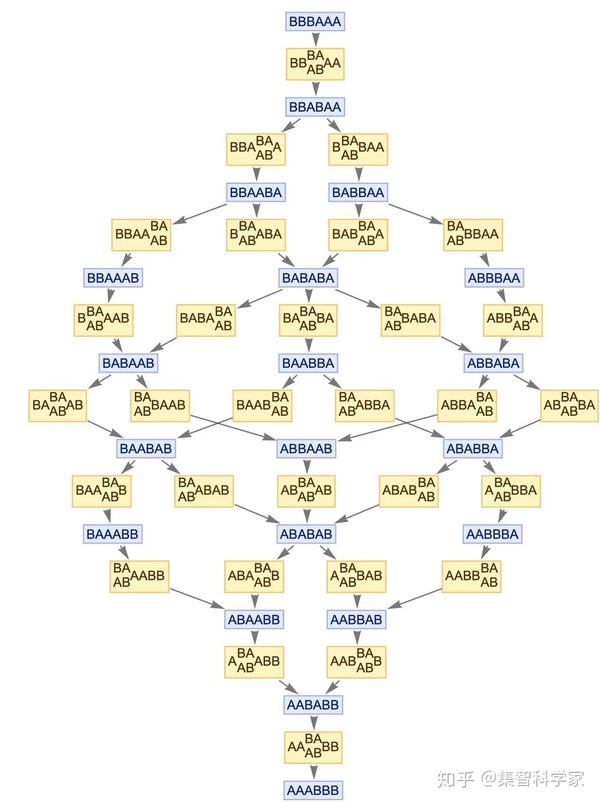
可以遵循许多不同的路径,这取决于规则在每个步骤中应用于字符串中的哪个 BA。但是我们看到的最重要的事情是,所有的路径最终合并,我们得到一个单一的最终结果:排序好的字符串 AAABBB。我们得到这个最终结果的事实,是这个规则的因果不变性的结果。在这种情况下,有一个最终结果(而不仅仅是永远进化),因果不变性基本上说:不管你做所有更新的顺序是什么,你得到的结果总是一样的。
在试图找到一个基础物理模型的背景下,我引入了因果不变性,并且我已经说过,它对于相对论和量子力学来说都是至关重要的。但是实际上,在数学、数学逻辑和计算机科学中,因果不变性的含义已经以各种不同的形式出现过了(它最常见的名称是“汇合”(conflunce),尽管这个名称与我所说的因果不变性之间有一些技术上的区别)。
考虑展开一个代数式,比如 (x + (1 + x)²)(x + 2)²。你可以先展开一个幂次项,然后再做乘积。或者你可以先乘上这些项。不管你按照什么顺序执行这些步骤,都会得到相同的标准形式(在这个例子中,Mathematica 告诉我是 4 + 16x + 17x² + 7x³ + x^4)。这种顺序的独立性本质上是因果不变性。
这里还有一个例子。想象你有一些递归定义,f[n_]:=f[n-1]+f[n-2](其中f[0]=f[1]=1)。现在计算 f[10]。首先你得到 f[9] + f[8],但是你接下来要做什么呢?你计算 f[9] ,还是 f[8] ?然后呢?最后,没关系,你总是能得到 55。这是另一个因果不变性的例子。
当人们考虑并行或异步算法时,如果有因果不变性是很重要的。因为这意味着一个人可以按照任何顺序做事——比如说,深度优先,广度优先,或者其他任何顺序——而且总是得到相同的答案。这就是我们上面提到的排序算法的情况。
好的,现在让我们回到因果关系上来。下面是用于排序过程的多路系统,注明了所有路径的所有因果关系:
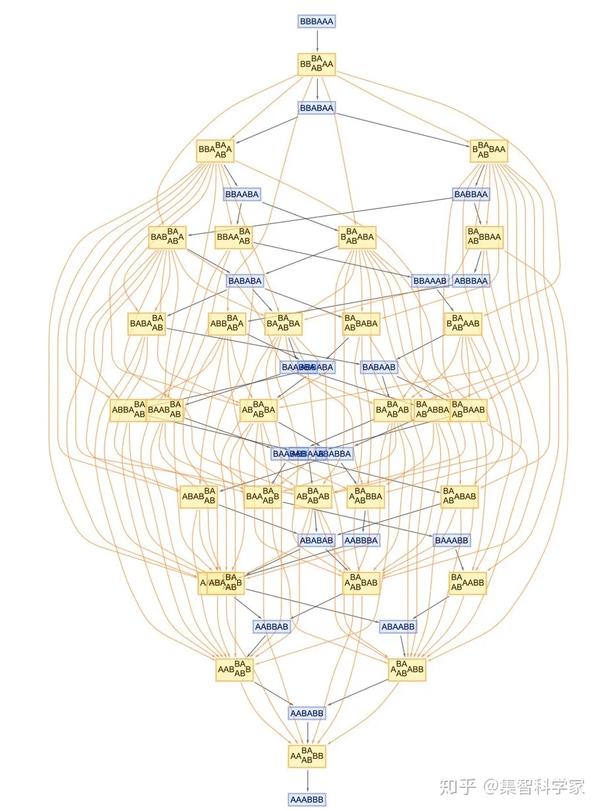
是的,一团乱麻。但由于存在因果不变性,我们知道一些非常重要的事情:这基本上只是同一个因果图表的许多复制品——一个简单的网格:
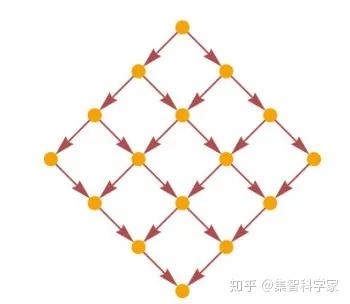
(顺便说一句——如图所示——这些副本之间的交叉联系并不是微不足道的,稍后我们将看到它们与相对论和量子力学之间的深层联系有关,这种联系可能在黑洞的物理学中表现出来。但是我们以后再说这个......)
因此,应用排序规则的每种不同方法,都应该给出相同的因果图。这里有一个例子来说明我们如何应用这个规则,从一个特定的初始字符串开始:

但是现在让我们来看看因果关系的图表,我们看到它只是一个网格:
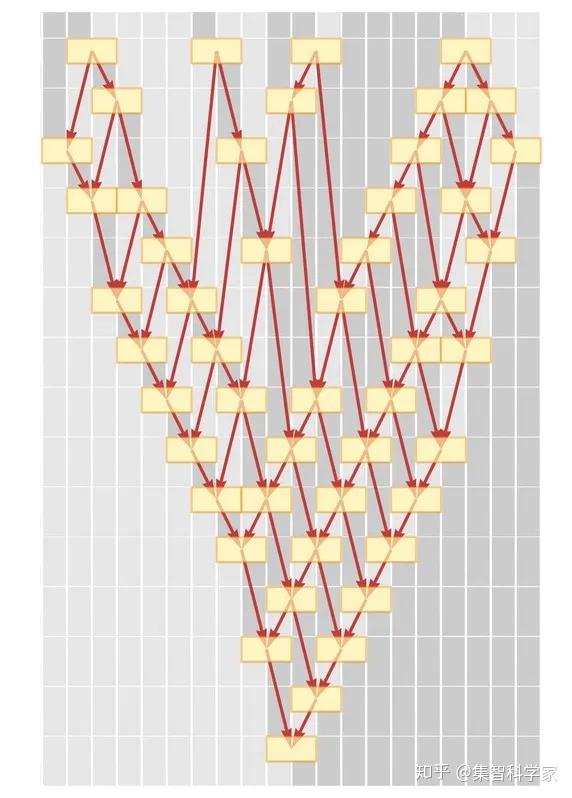
以下是其他三种可能的更新顺序:
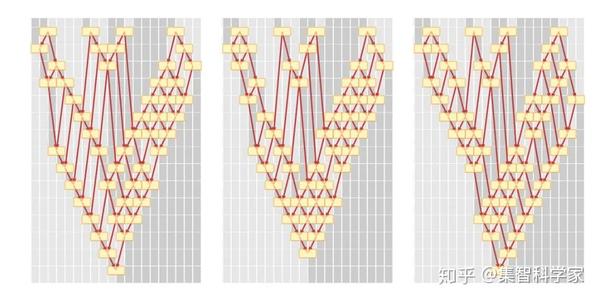
但是现在我们看到了因果不变性的实际应用:即使不同的更新发生在不同的时间,更新事件之间的因果关系图总是相同的。通过一个非常简单的例子,我们已经看到了这一点,现在我们准备谈谈狭义相对论。
编译:刘金国、Leo、eBeam、Jin
编辑:张爽
推荐阅读
搜索公众号:集智俱乐部 加入“没有围墙的研究所” 让苹果砸得更猛烈些吧!
评论:
小姜爱数学: 从文字流畅程度上说,译文至少可以打八十五分 (6 赞)
集智科学家 -> 小姜爱数学: 赞!
HanceWu4464 -> 小姜爱数学: 但是有的内容和原文不一样啊... (1 赞)
知乎用户XuM8KI: wolfram大大觉得在YouTube上做每周科普不过瘾,然后写这么多[赞同] (4 赞)
知乎用户: string,字符串,弦[思考][思考][思考] (3 赞)
CERN: 看了,确实是跨时代的思想,真实性另谈,我觉得这是我最初对理论物理脑海中的样子,非常精彩。不过还只是个小的框架,不知道以后会发展成什么 (3 赞)
庞加莱: 终于开始认真走老子《道德经》思维范式了 (3 赞)
HanceWu4464: 翻译的不太行啊 有修正可以提交么
集智科学家 -> HanceWu4464: 可以说出你觉得不行的地方,我们沟通一下~确实存在一些小问题。
HanceWu4464 -> 集智科学家: 什么是空间那段之前 那段问怎完全混乱 换个人看一遍吧
集智科学家 -> HanceWu4464: 可以私信给我们
sungine漾离: 很遗憾的一点是Stephen Wolfram受限于目前的物理学框架,没有把更多的存在作为物理量一起用来解释它的混沌系统,否则可能会更接近真理 (1 赞)
胡良: 如果你见到,量子三维常数理论,你就会明白什么是真正的物理学。 (1 赞)
scott.cgi:
确实翻译的很不错,阅读体验很流畅。
因果不变性,说明宇宙具有确定的起点与终点,还有确定的演化方向(或说计算方向),或许应该反过来说,因为有确定的起点与终点,才有因果不变性。 (1 赞)
壳谣: 素质三连,慢慢看 (1 赞)