多元函数中可微与可导的直观区别是什么？ - 马同学的回答

数学, 微积分, 函数, 高等数学, 高等数学 (大学课程)

在(一元或多元)函数中，可导和可微的内在联系与区别的本质是什么？为什么会单独对这两个概念加以区分？在数学定义推导背后的，函数可导却不可微的外在直观感受是什么？

在多元的情况下，可微可导的关系要比在一元情况下复杂，但是只是要复杂一些，如果我们从一元开始去理解，你会发现并不困难。

这篇文章主要阐述以下三个概念：

• 偏微分
• 偏导数
• 全微分

全导数这里暂时不讲，看名字好像和全微分关系很大，其实和“方向导数”的关系更大，所以留到讲“方向导数”的时候再一起来说。

1 偏微分

在一元函数中的微分就是函数的切线：

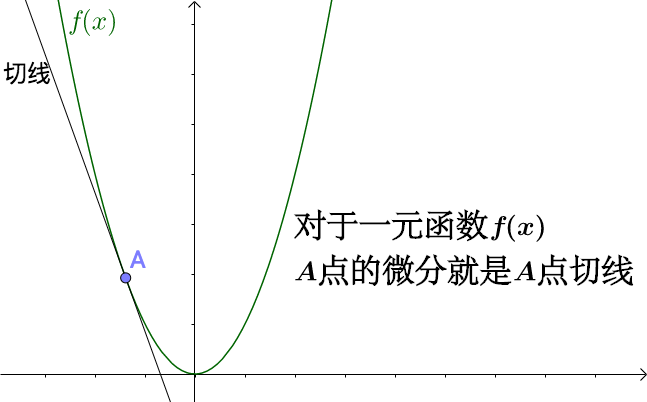
关于微分就是切线，我写的很多文章（比如我最近的 如何通俗解释全微分？ ）都希望大家可以理解这一点，虽然要严格讲清楚需要微分几何、流型的知识，但是我认为掌握了这一点对于我们学习微积分很有帮助。

我们发挥一下空间想象力，把它从平面中拽出来，进入三维空间：

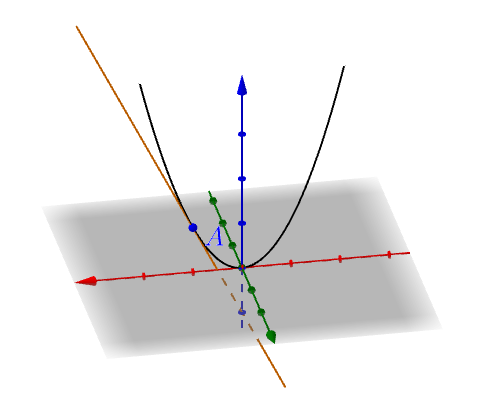
之前是平面曲线，现在是空间曲线。切线仍然是切线，微分仍然是微分。

我们再想象一下，其实这个空间曲线是 这个空间平面与 这个空间曲面的交线：

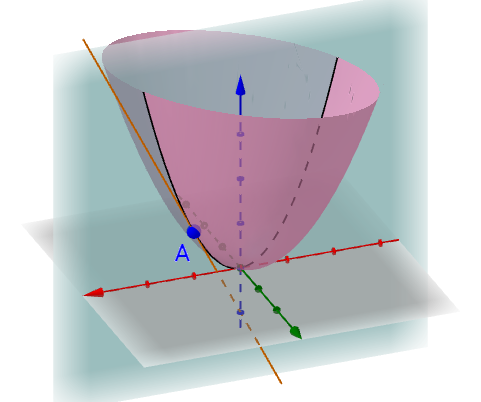
我们就把这个切线称为 对于 的偏微分。为什么是对于 的呢？因为这是 与 的交线，在这条线上无论点怎么变化，都要满足 ，即 是常数不会变化。

你来玩玩下面这个互动操作就知道了，点在线上变化只会改变 和 ：

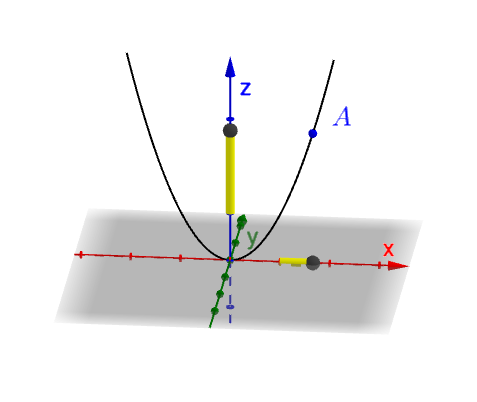
此处有互动内容，点击此处前往操作。

理解了这个，就可以举一反三，所有 （ 为常数）的平面与 的交线都是满足刚才说的特点：

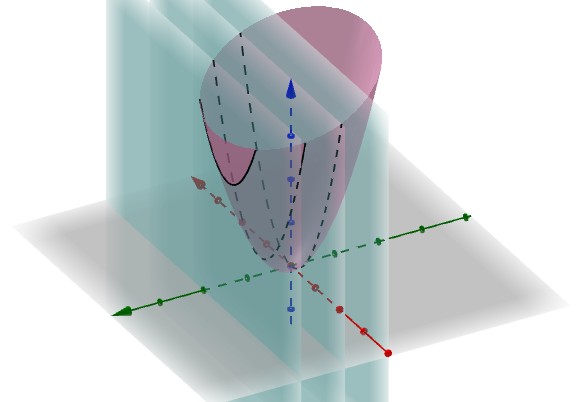
这些交线上的点的切线都是 关于 的偏微分。

当然，如果 与 （ 为常数）得到的交线，这些交线的切线就是 关于 的偏微分。

总结，偏微分就是：

• 固定 ，变换 得到的就是 关于 的偏微分
• 固定 ，变换 得到的就是 关于 的偏微分

2 偏导数

偏微分理解了偏导数就好理解了，就是偏微分的斜率，现在你应该可以明白为什么我们在求 对于 的偏导数的时候，我们把 当作常数来看待了吧。

只是有一点需要说明，在三维空间中角度可以有不同的定义，计算斜率的时候我们是看下面这个 角：

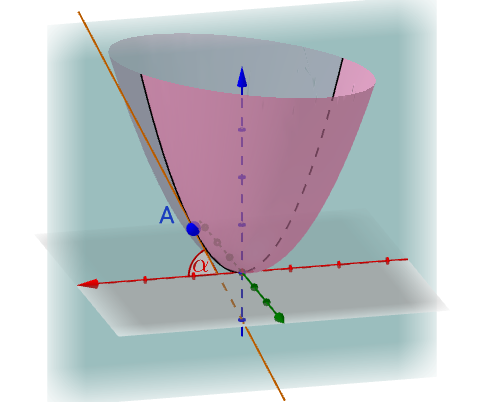
总结，偏导数就是偏微分的斜率。

3 全微分

其实，不光是 或者 这样的平面可以和 相交得到交线，所有和 平面垂直的平面都相交得到交线，这些交线都会有切线（微分）。

这个平面相交得到的交线：

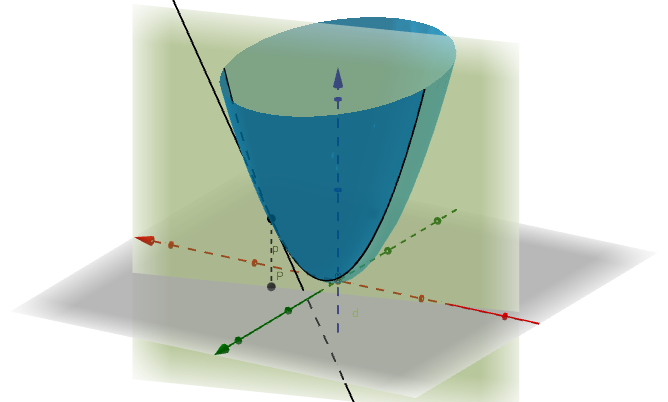
这个平面也可以：

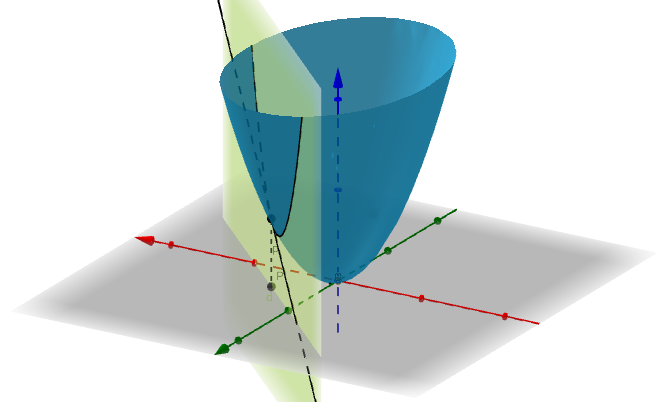
总之，应该是360°无死角，自己动手试试：

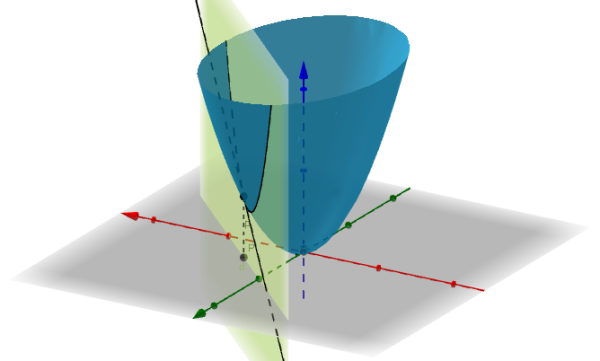
此处有互动内容，点击此处前往操作。

如果这些切线都存在，并且这些切线（无数条）还都在同一个平面上（平面不是曲面），那么得到的这个平面就是全微分（也叫做切平面，或者说切空间）：

此处有互动内容，点击此处前往操作。

总结，全微分就是：

• 360°微分都存在
• 并且这些微分要共面，得到的就是全微分

4 全微分与偏导数、偏微分的关系

根据全微分的定义，如果全微分存在，那么偏导数、偏微分一定存在。

但是反过来不一定成立，即偏导数、偏微分存在，全微分不一定存在。因为偏导、偏微分只是 或者 方向的导数、微分，而全微分要求的是360°无死角。

举个例子，看这个 ：

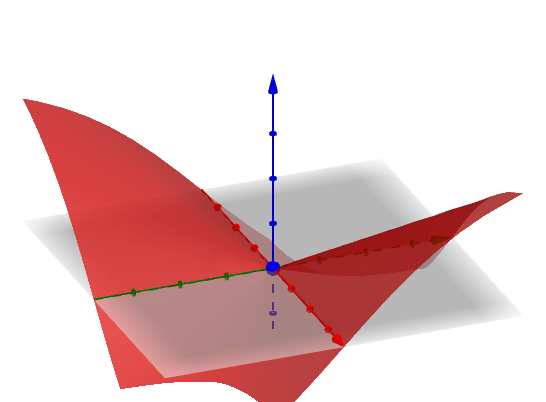
我们考察这个函数在 点的全微分和偏微分的情况。

与 的交线是：

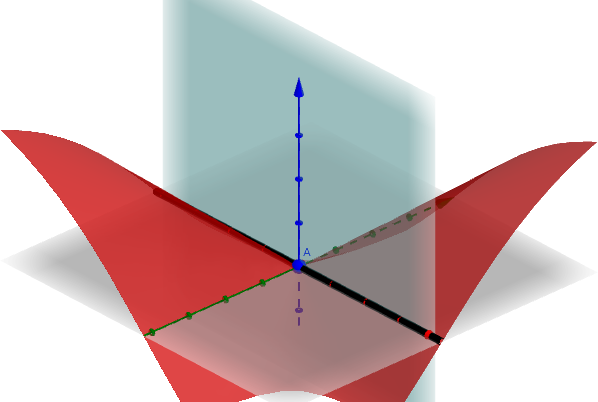
平面与曲面所交曲线与 轴重合：

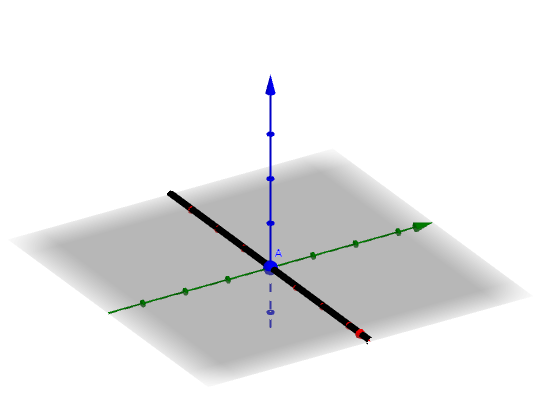
在 点的微分（切线）很明显，就是交线（ 轴）自身，因此关于 的偏微分存在。

但是 与 的交线是：

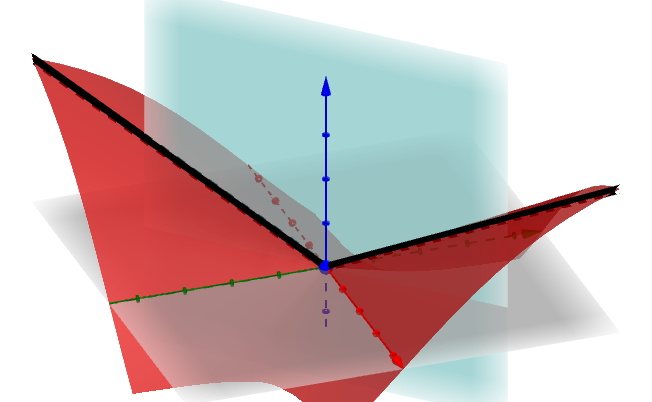
在 点形成了一个尖点，很显然此时的微分不存在：

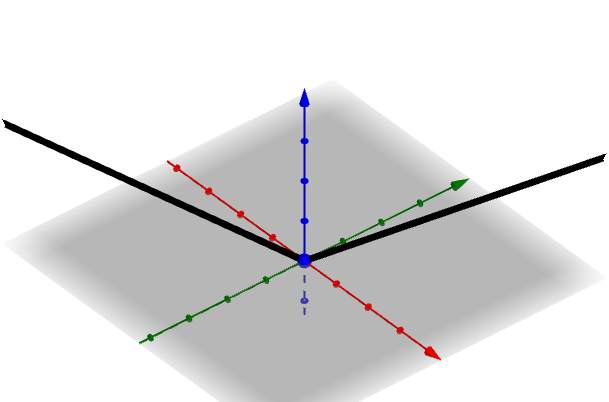
因此，全微分不存在。

总结，全微分与偏导数、偏微分的关系：

• 全微分存在偏导数、偏微分一定存在
• 偏导数、偏微分存在全微分不一定存在

默罕默德·赵四:
你的回答简直完美契合我的考研复习进度😂白天还在思考消化这块内容 晚上就看到你写的答案了 而且日期很新鲜～ (29 赞)

　　
马同学 回复 默罕默德·赵四:
迷之契合 (9 赞)

00000000000000.1:
整个zhihu上最好的回答。专业，准确而且让人理解。stackoverflow上也不多见。 (14 赞)

石黛青:
在学数学分析的大一新生 刚好学到这里 讲得很好 谢谢啦 (12 赞)

万叶:
请问，如果一个多元函数某点得各个偏导数都存在，那么此多元函数在此点一定可微，这句话为什么错了啊。

　　
马同学 回复 万叶:
偏导数要连续才可微

　　
Gimosolv 回复 马同学:
偏导数连续函数可微是个充分条件。可微函数的偏导数不一定连续。

　　
马同学 回复 Gimosolv:
对的，我用词不严谨。谢谢指正。

　　
马同学 回复 万叶:
偏导数要连续才是可微的充分条件，光是偏导存在是推不出可微的。

　　
Captain 回复 马同学:
求证明偏导数在某一点连续，可以推出函数在该点可微。😂😂 (1 赞)

　　
马同学 回复 Captain:
证明书上就有，只是怎么直观我还需要考虑。 (1 赞)

　　
Captain 回复 马同学:
嗯我知道书上给出了一个证明，只是那个有个小地方还不太明白。

青春:
这是什么画图软件～ (1 赞)

　　
马同学 回复 青春:
GeoGebra (6 赞)

　　
ktwong 回复 马同学:
書(同濟)上說,偏導數存在并不一定保證可微,是因為用偏導數表示的多元函數增量與真實多元函數增量的差不一定就是較多元函數自變量增量趋於零的高阶無穷小,這個在幾何上的解釋為什麼就是你所說的360度所截曲線斜率都存在?
這個代數與幾何關係應該怎樣理解?

　　
马同学 回复 ktwong:
偏导只有两根直线，这两根直线只能确定一个面，只有可微，这个面才能表示，你说的真实多远函数的增量。

　　
ktwong 回复 马同学:
細心翻看了一下推導，通過多元函數全增量數學表達式的變形，使得能利用一元函數拉格朗日中值定理，從而把多元函數的全增量用其偏導數表示出來，并最終構造出能近似曲面的切面。推導過程能看懂，只是覺得偏導數連續的那個條件引入很別扭。用偏導數表達出多元函數的全增量後，怎麼會想到要有偏導數連續呢？能不能解釋一下？不勝感激！！！！

　　
ktwong 回复 马同学:
推敲了一下書(同濟)上推導的幾何意義，之所以要連續應該是因為多元函數的微分形式僅表明能在多元函數的某維度的某截面上找到適合點的偏導數以用於表示多元函數的全增量，故多元函數可微，僅表明函數在該維度上有偏導存在，并不保證該維度上所有截面所得的偏導存在，因此需引入偏導連續條件，以保證任意維度的任意截面的偏導數都能存在，從而保證必能取得能用於表示多元函數全增量的偏導數。這樣理解不知對不對

刘宇昊:
同学能再补充一下偏导连续性和全微分的关系吗 (1 赞)

　　
马同学 回复 刘宇昊:
在思考怎么直观。

　　
茶茶狗 回复 马同学:
请问最后这个不可微的例子看起来原函数分别与y=0和x=0的交线都是直线，那么它们在零点对应的两个偏导应该都是常数，也就是固定值了，那么就应该是连续的。为什么最后函数在零点还是不可微呢？ (1 赞)

　　
唐航 回复 茶茶狗:
和你抱有同样的疑问

　　
唐航 回复 茶茶狗:
好吧，看书懂了，我们对偏导连续的概念有误解。偏导在某点连续还要求偏导在该点的邻域内存在 (1 赞)

小蜗牛:
看书搞不懂又遇到您的答案了😂
我刚看时就不能太理解根据全微分公式△Z=A△x+B△y+o（p），中△Z是不是表示面积的增量，那为什么会用x方向上的增量加上y方向上的增量呢，这个增量的几何意义是什么？ (1 赞)

　　
马同学 回复 小蜗牛:
增量是代数意义。几何意义就是切点附近的曲面

　　
小蜗牛 回复 马同学:
我现在脑子里想象的是一个面的增加的量，怎么能用两个边的增量表示呢，我应该想错了吧(:з」∠)

　　
马同学 回复 小蜗牛:
就是一个二元函数

　　
小蜗牛 回复 马同学:
谢谢你哈，让我能在脑子里想到画面 ( 'ω' )

Edithnia:
回答真的太棒了，这才是知乎的精华，答主就是知乎的未来，就是中国的希望 (3 赞)

　　
马同学 回复 Edithnia:
谬赞了，继续努力。

何志:
期待解释为什么切线在同一个平面~ (2 赞)

　　
马同学 回复 何志:
这之前还有好几个概念需要完成讲解。 (1 赞)

Luyoung:
不错 (2 赞)

from: https://www.zhihu.com/question/23468713/answer/153515600