如何解释洛必达法则? - 马同学的回答
title: 如何解释洛必达法则? - 马同学的回答
url: https://www.zhihu.com/question/28862411/answer/123019423
author: 马同学 (matongxue)
voteup: 3330 赞同
thanks: 1205 感谢
create_date: 2016-09-21 17:23:23
edit_date: 2016-09-21 17:23:23
fetch_date: 2020-02-26 14:17:57
count: 约 8509 字
version: 1
话题:
数学, 高等数学
问题描述:
(无)
回答:
17世纪的贵族子弟洛必达曾经说过:人这辈子一共会死三次。
-
第一次是你的心脏停止跳动:那么从生物的角度来说,你死了。
-
第二次是在葬礼上:认识你的人都来祭奠,那么你在社会上的地位就死了。
-
第三次是在最后一个记得你的人死后:那你就真的死了。
为了知行合一,洛必达从数学家伯努利手中重金买下了一个知识产权,伯努利收获了金钱,也付出了后悔。
这次交易的内容就是我们今天要讲的,以洛必达的名字命名的 洛必达法则 。
1 洛必达法则
洛必达法则(l 'Hôpital's rule)是利用导数来计算具有不定型的极限的方法。这法则是由瑞士数学家约翰·伯努利(Johann Bernoulli)所发现的,因此也被叫作伯努利法则(Bernoulli's rule)。
维基百科
不严格的说,洛必达法则就是在 型和
型时,有
。
可见,洛必达法则最犀利的是大大简化了极限运算。这种化繁为简的技术手段从来都是深受喜爱的。
这篇文章我们主要回答一下两个问题:
-
为什么洛必达法则对于
型和
型生效?
-
洛必达法则对于别的类型是否生效?
1.1 构造关键函数
我们令 ,为了阅读顺畅,这个函数我要多解释下。
对于一般我们接触的函数,比如 ,根据函数定义,这是一个
的映射:
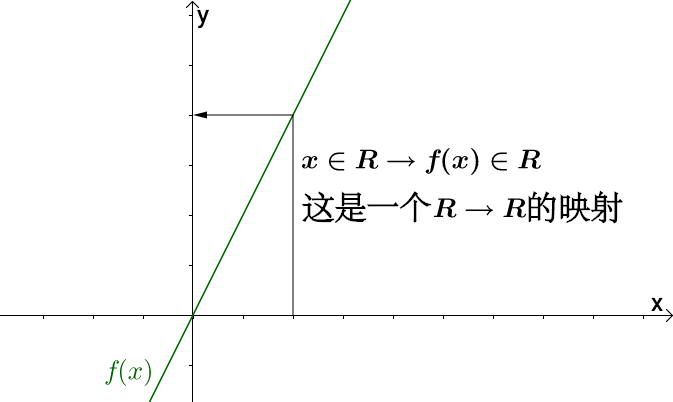
而 是一个
的映射:
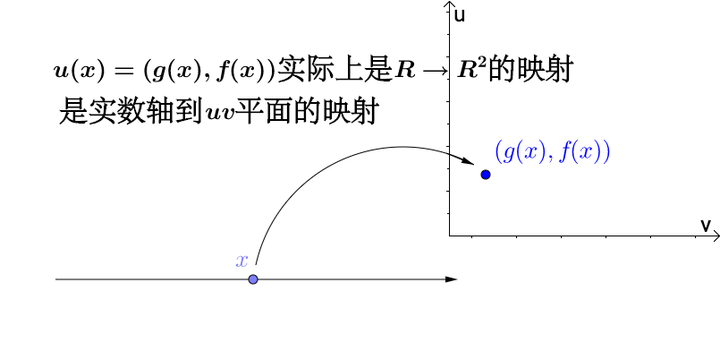
可以如下表示:
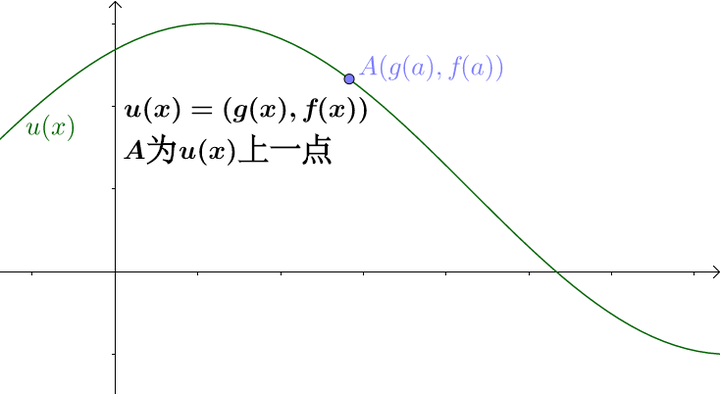
做出 点的割线:
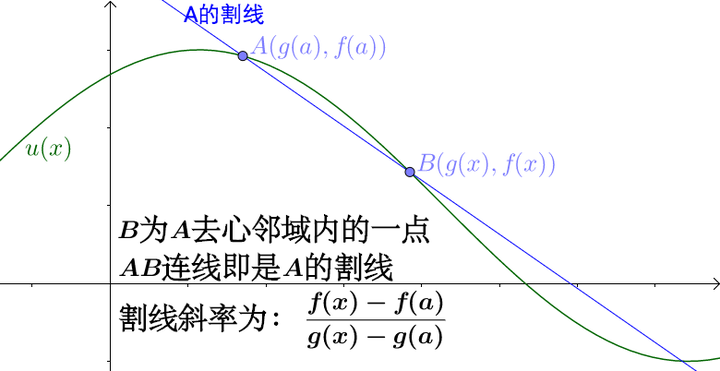
割线的极限即是切线,大家可以感受一下:
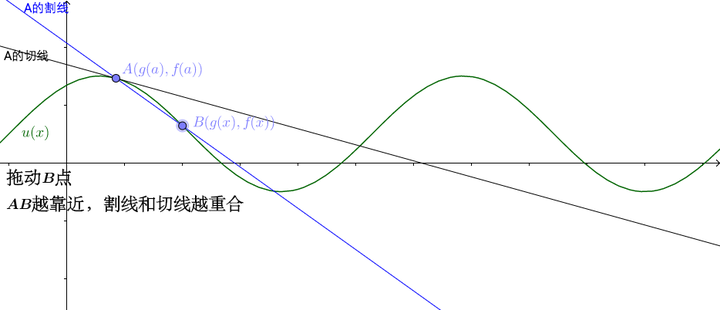
此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。
所以可以得出切线的斜率即导数为:
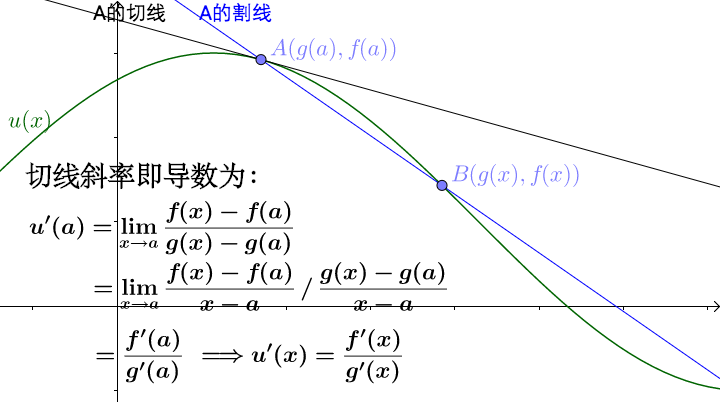
通过坐标轴的原点 连接
点,马同学把这个连线称为原点线:
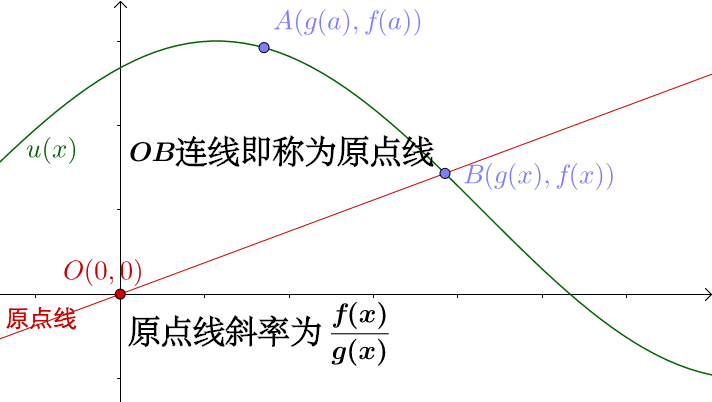
通过构造关键函数 我们得到两个的结论:
- 原点线斜率为
根据洛必达法则: 。可见,构造关键函数之后,我们已经有了
和
,剩下的就是看这两者什么时候极限相等了?
1.2 型
我们让 曲线可以经过
点:
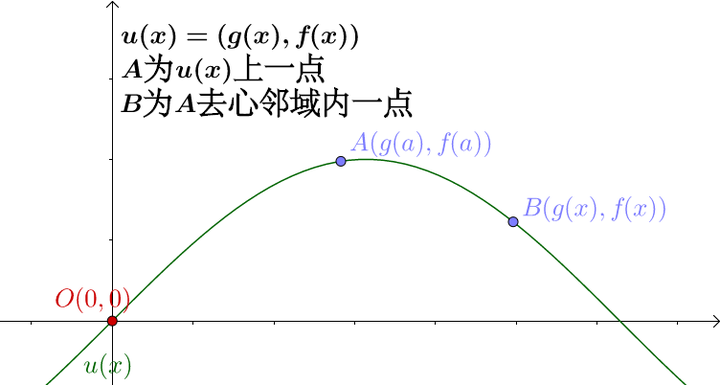
分别做出割线和原点线:
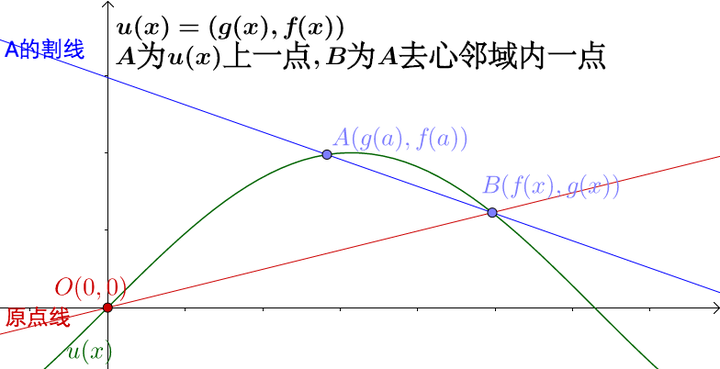
容易观察到, 点越靠近原点,割线和原点线越接近:
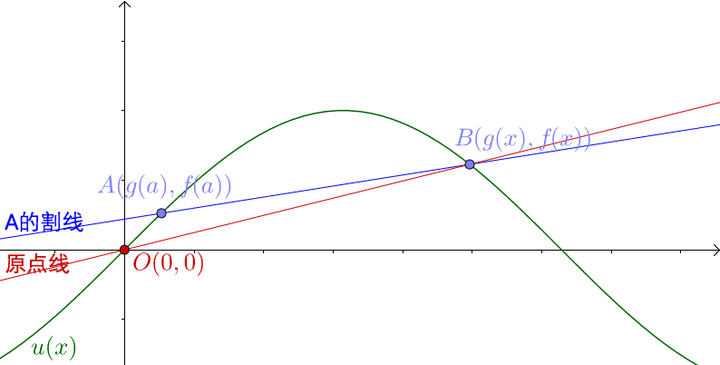
可以动手试试:
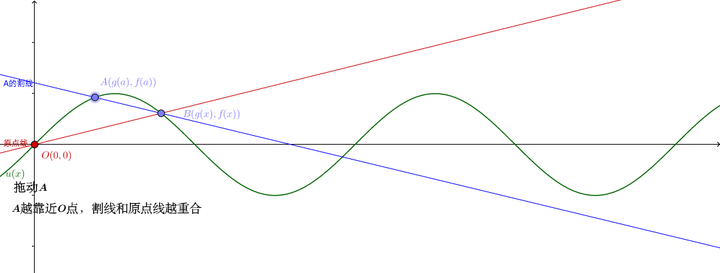
此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。
点和
点重合时,割线就是原点线:
点和
点重合时,割线斜率就是原点线斜率,即
。 根据割线的极限即切线,有
,根据之前的结论有
,所以
,所以有
,即洛必达法则。
需要说明一点:
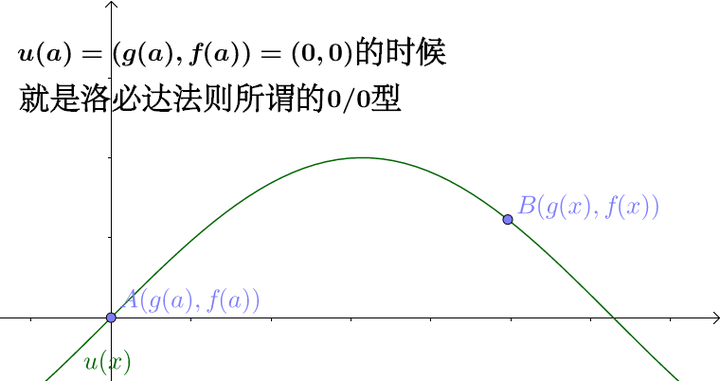
可见,洛必达法则对 型可以生效。
1.3 型
在欧式几何中,两条线的斜率要相等,只有两种情况,重合或者平行。
这就是 型为什么适用于洛必达法则的原因,我们来一起推导一下。
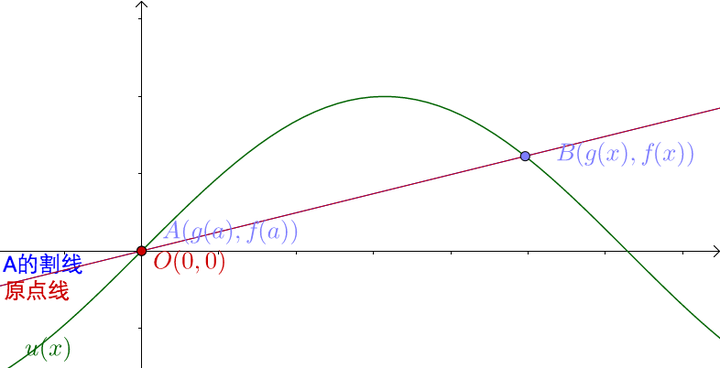
首先 要换一下,必须得有
点:
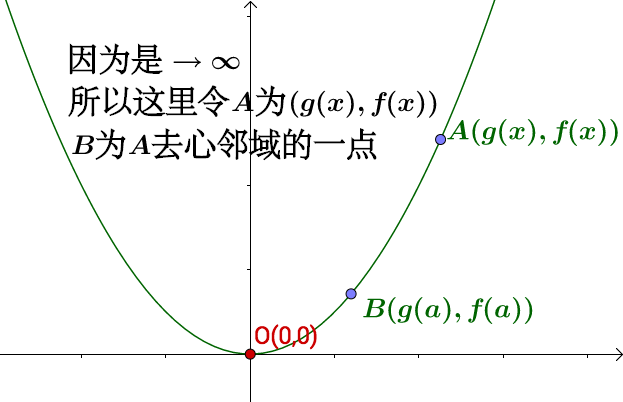
画出割线和原点线:
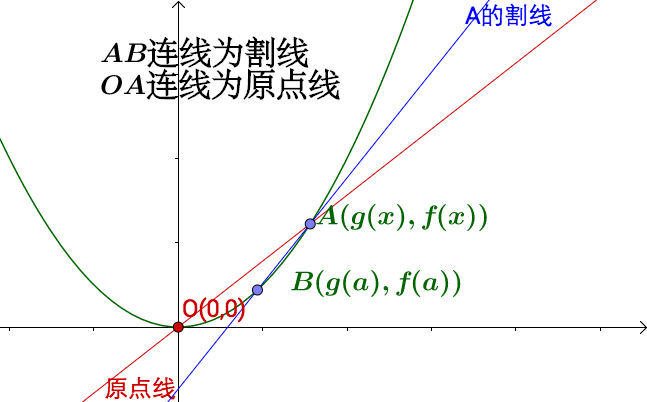
当 时,割线和原点线趋向于平行:
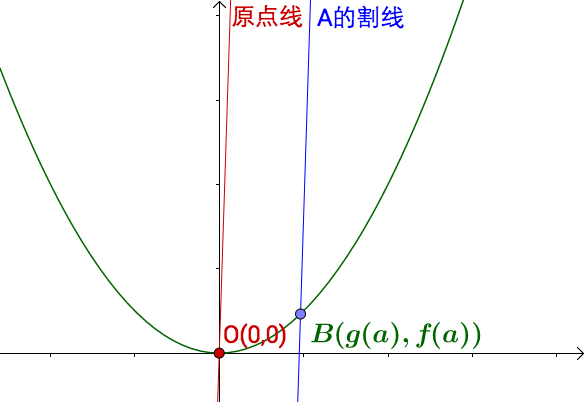
顺便说一下,这里比较诡异的地方是,割线和原点线一直交于 点,但是当
时居然两者可以平行。其实我们可以说两条平行线交于无穷远点,至于无穷远点能否到达又是另外的问题了。
你也可以动手试试
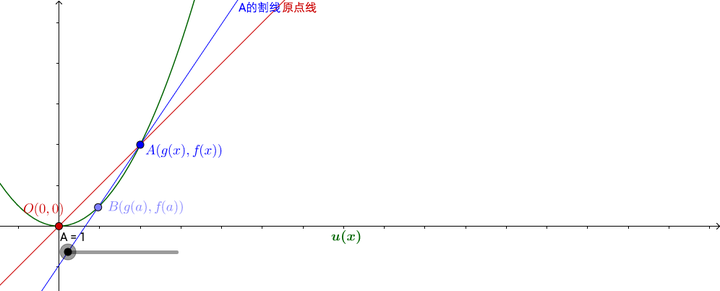
此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。
同样说明一下, 意味着是
型。
根据 型的推论的思路,洛必达法则对于
型也生效。
1.4 结论
所以洛必达法则生效的原因是:
-
型:割线和原点线重合
-
型:割线和原点线平行
2 扩展洛必达法则
这里就是要回答洛必达法则对于别的类型是否生效的问题。
2.1 洛必达法则总是有效的函数
令 ,
,可以用两种办法求极限:
-
约分:
-
洛必达法则:
根据第二种解法,意味着这两个函数总是适用洛必达法则。
我们构造 ,画出图像:

2.2 洛必达法则的扩展
所以,只要原点线和割线斜率相等,就可以运用洛必达法则,对洛必达法则的扩展让我们把它称为马同学法则吧:)
不过就实际应用来说,还是 型和
型最实用,但是好歹让马同学发明了一个马同学法则,希望可以像洛必达法则一样名垂千古。
3 最后
我想,洛必达先生真的是因为这场交易不朽了。
评论:
the N:
所以洛必达至今未死,每一个学高数的人都在为他续命 (773 赞)
李翔宇 回复 the N:
猝不及防 (71 赞)
猫咪没睡醒 回复 the N:
一尺之锤 (30 赞)
藤原妹红 回复 the N:
还有因为江苏理数高考 (16 赞)
锁清秋 回复 the N:
那句话应该是取自《生命的清单》,大卫·伊格曼,原句描写得更准确些 (6 赞)
郝晓斌 回复 the N:
最近新出的寻梦环游记故事逻辑就是他的第三次死亡原理。 (4 赞)
千江有水 回复 the N:
可是要了不懂高数的人的命눈_눈
(开个玩笑) (4 赞)
濯缨 回复 the N:
现在高考也要涉及了。
猫咪没睡醒:
为前三句话点赞 (116 赞)
一只蝙蝠侠 回复 猫咪没睡醒:
这个是中国大学MOOC公开课的原话,基本上就是照搬的 (8 赞)
熊大 回复 猫咪没睡醒:
该评论已删除 (5 赞)
usk d:
我擦,原来是买的 (82 赞)
Houdini.Z 回复 usk d:
屌爷也来学数学啊
麦克雷霆滚滚滚滚 回复 usk d:
DIO!!!!
麦克雷霆滚滚滚滚 回复 usk d:
欧拉欧拉欧拉欧拉欧拉欧拉欧拉!
被盗无解绑请拉黑:
伯努利真的没必要后悔……每个学流体力学的同学都在为他续命 (63 赞)
一只菜鸡 回复 被盗无解绑请拉黑:
伯努利具体来说是一个大数学世家。洛必达法则提出者是约翰伯努利,而流体力学中伯努利原理命名则源自是老约翰的儿子 丹尼尔伯努利。 (13 赞)
被盗无解绑请拉黑 回复 一只菜鸡:
你一说我就想起来确实是,当初课上是这么说的。这就是靠家族续命了 (4 赞)
吃货小谢 回复 被盗无解绑请拉黑:
每个学数学和统计学的也在给他续命啊!说真的我觉得Bernoulli要有名的多,他其实没亏,用一点自己不需要的名气换钱~ (6 赞)
一身缺点 回复 被盗无解绑请拉黑:
不是同一个伯努利吧……
如果您说的是流体力学里的“伯努利方程”的话,那个是丹尼尔·伯努利,我印象里是18世纪初才出生的人;
而“洛必达法则”的那个伯努利,好像是约翰·伯努利;
他们俩是一个家族的人,具体关系我不记得了。 (1 赞)
马同学 回复 一身缺点:
祖传老中医
独上寒江 回复 一身缺点:
我记得是个大家族,去维基看了一下:
雅各布·伯努利(也做詹姆斯或雅各,1654–1705),在概率方面的贡献突出,以伯努利分布而闻名。
约翰·伯努利(1667–1748),雅各布的弟弟,以最速降线而闻名,教授过欧拉。
小尼古拉·伯努利(1695–1726),约翰的大儿子
丹尼尔·伯努利(1700–1782),约翰的小儿子,在流体力学方面贡献突出,以伯努利定律而闻名。
大尼古拉·伯努利(1687–1759),雅各布和约翰的侄子。 (8 赞)
爱吃猫的鱼丶 回复 被盗无解绑请拉黑:
流体力学是他的儿子小伯努利搞出来的 (1 赞)
接受采访 回复 被盗无解绑请拉黑:
不是一人
乌尔比诺:
该评论已删除 (21 赞)
amec 回复 乌尔比诺:
利 (5 赞)
李翔宇 回复 amec:
国 (5 赞)
zhuqizhen 回复 李翔宇:
家 (3 赞)
梁Chuck 回复 zhuqizhen:
生 (3 赞)
周涛 回复 amec:
国
周涛 回复 amec:
国
阿攘 回复 梁Chuck:
死
王赟 Maigo:
无穷比无穷型解释得好像有问题……最后应该是A点趋于无穷的时候,切线和原点线斜率趋于相等吧。而且u曲线不必通过原点。 (6 赞)
马同学 回复 王赟 Maigo:
你好。这个问题我考虑过,切线、割线、原点线都会在无穷远点平行,但这么处理一方面是统一模型,一方面是切线在图上画不出来,因为它的x坐标也是无穷远。u曲线确实没有必要过原点,只需要有无穷点就可以了。
王赟 Maigo 回复 马同学:
是怎么统一的呢?洛必达法则的一边是f'(x) / g'(x),这就是切线的斜率,你怎么就把切线给绕过去了呢?
马同学 回复 王赟 Maigo:
该评论已删除
王赟 Maigo 回复 马同学:
割线有好多条,切线是割线的极限,不是随便拿一条割线就跟切线平行的。 (1 赞)
马同学 回复 王赟 Maigo:
A趋于无穷的时候割线、切线、原点线都平行。进一步,割线的极限就是切线,而洛必达法则是对极限生效的,所以并非绕开切线,而是有个割线和原点线平行之后,两边取极限。
王赟 Maigo 回复 马同学:
割线是由A,B两点决定的。A点趋于(无穷,无穷)没问题,你的B点是怎么取的? (1 赞)
马同学 回复 王赟 Maigo:
你说的对,但是在无穷远点的切线和割线都平行,或者说交于无穷远点的线都平行或重合。所以B点可以随便取 (1 赞)
王赟 Maigo 回复 马同学:
我顺着切线趋近于原点线的思路,并没有想出来……所以对于无穷/无穷型,还是分子分母各取倒数,化成0/0型比较有说服力。你对0/0型的解释还是很有启发性的! (1 赞)
Silence:
非常感谢。不过这些是如何构想出来的? (6 赞)
马同学 回复 Silence:
数学是个游戏,只要你喜欢,就可以好好去玩。怎么构想出来的?也就是玩出来的。 (31 赞)
Silence 回复 马同学:
谢谢你的回复,看了你的很多回答,感到很有帮助。也感谢你能抽出时间服务大家! (6 赞)
马同学 回复 Silence:
谢谢支持,成人便是成己。我也是在学习。看书学习和把知识讲述出来,效果完全是天壤之别。 (9 赞)
Lei Renee 回复 马同学:
答主一定智商很高 (1 赞)
马同学 回复 Lei Renee:
谬赞了,不过是有几分呆气罢了。
许木木 回复 马同学:
这让我想起了一本书,是讲游戏与学习之间的关系。然后最强大脑中美对决片段,美国少年说过类似的话。
beta:
u(x)是二元函数,不能用u'(x)表示那条曲线的斜率吧。 (6 赞)
马同学 回复 beta:
是可以的 (1 赞)
Dedicatus545 回复 beta:
u(x)更像参数函数吧 (2 赞)
李心 回复 beta:
我也有同样的问题
大阿昊 回复 beta:
应该用u’(x。)
莫小北:
从他老师那买来的 (8 赞)
王大可:
岂 (6 赞)
王二 回复 王大可:
因 (5 赞)
落子无悔 回复 王二:
祸 (1 赞)