变分法简介Part 1.（Calculus of Variations）

有限元分析（FEA）, 固体力学, 应用数学

1. 泛函数 (Functionals)

简而言之，泛函数是函数的函数，即它的输入是函数，输出是实数。而这个输出值取决于一个或多个函数（输入）在一整个路径上的积分而非像一般函数一样取决于离散的变量。这样说可能还是比较抽象，不过坚持看到下文的 Example 1 就可以更好理解了。

通常在变分法中，泛函数是一个积分，记做 。

其中我们想要通过选择被积函数 来最大化或最小化泛函数 的值。同时我们称 为拉格朗日函数(Lagrange function)。 可以是函数 和 各阶导数的函数(以下 均简写成 )。为了说明方便，我们先姑且设 是 和 的函数，所以我们可以进一步将泛函数 写成：

积分里面我用分号;将 和前面的 隔开代表 和 是 的函数。一般 和 的函数关系是已知的，所以想要最大或最小化泛函数，实际上是通过选择适当的函数 。

为了透彻理解这个概念，我们可以来看一个简单的例子。

_ _Example 1.__

一个最简单直观的例子是求两个固定点之间的最短路径。当然大家都知道两点之间直线最短，这里可以用变分法做出解释。

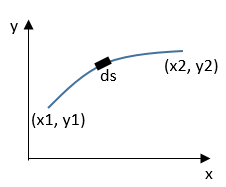
如上图所示路径是一任意路径，我们取区中一小段微元 ，可以容易计算微元断的长度为：

,即：

积分得到总的路径长度为：

这个例子中， 是泛函数， 是拉格朗日函数 ，我们想要找一个函数 使得泛函数 的值最小。这次Part 1.的任务就是为解决这个问题做准备。Part 2.中我们会用变分法证明这个 确实是直线的方程。

2. 泛函数的极值

这里重申下，泛函数 在区间 上的值取决于积分路径的选择，即取决于函数 的选择。我们有理由假设存在一个这样的 ，可以使得泛函数 取到极值。而在这个 附近的任意路径我们记做 。另外，我们假设 两阶可微。通过引入一个微小量 和一个任意可微函数 ，我们可以用 表示 :

这样做的好处是对于一个给定的 ，我们可以通过改变 的值来得到无穷多的路径，同时对于任何 ，当 的时候， 和 重合。

图像直观表示如下图：

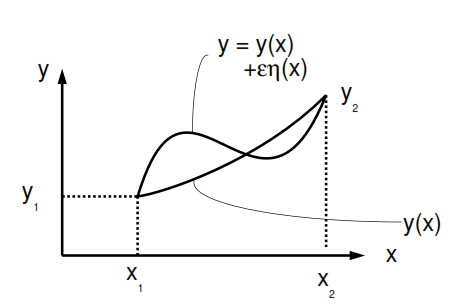
由于在边界条件的限制， 。这样就能保证 可以通过两个固定端点。

这时我们可以说， 所对应的泛函数 的值是泛函数 的极值。我们可以进一步用 表示 ：

虽然 未知，但是根据之前的合理假设， 是一个存在的确定函数。所以根据上式，如果给定一个特定的 ， 的变化只取决于 的变化。所以我们现在可以把 看做是 的函数。用泰勒展开公式将 在 处展开得到：

很明显，当 时， ,带入上式可得到：

这里我们记 ，并称之为一阶变分。同理二阶变分为 。

（这里插一句变分和微分的区别。变分在上图的直观解释是 和 在竖直方向上的距离，称之为 ，所以这个差是在同一个x上计算的。而微分则是由于x的微小变动引起的y的变动。）

然后我们可以类比求函数极值时的做法。求函数极值时，我们会令函数的一阶导数为零。这里同样，为了求泛函数 的极值，我们令一阶变分 。现在我们计算化简 :

因为 , 不难得到： , ,另外我们有
又因为当 时， ,将这些式子带入原式可以得到：

终于到最后一步啦，分部积分一下得到：

另 就可以解得最小化泛函数的y啦。我们注意到 有两个部分。对于第一个积分部分，由于 是任意的，所以要想使这个部分等于零，需要保证 ：

( )

这就是传说中的欧拉-拉格朗日方程(E-L equation)。

而第二部分等于零则是边界条件。

在Part 2.， 我们会以用这次介绍的内容和上述方程解决两点之间直线最短的问题为开头，继续介绍变分法。

---------------------------------------------------------------------------------------------------------------------------

注[1]:

假设 和 是给定的常数， 是一个特定的在 上连续的函数，那么如果对于任意连续可微的函数 都成立 ，则 ( )。

（任意函数和一个非零的特定函数的乘积仍是任意函数，由于无法保证任意函数的积分是零，所以这个特定函数必须在这个区间上恒等于零使得乘积为零，这样可以保证积分为零。）

知乎用户: 没来得及看，先赞一个。这个领域写的人少 (13 赞)

夏筠峥: 最后一步分部积分的时候，dv=?y' -> v=?y, 这部不是很能明白，为什么这里变分可以当做微分 (1 赞)

Dr.Stein -> 夏筠峥: 这里没有把变分当做微分，变分一直没有动，只是用分部积分把微分转移了，评论不好打公式，有需要我可以手写拍照私信发你具体过程 (2 赞)

夏筠峥 -> Dr.Stein:

我是按照公式∫udv=uv-∫vdu，理解的，如果我没有理解错的话，这里的一个δy'当成了dy'去去进行分部积分了
（如果您能发私信也可以，我觉得在这里讨论可以让相关读者都看到，然后搜狗输入法可以打出来各种符号，比如拼音积分就有积分符号，拼音delta就有变分符号） (17 赞)

Dr.Stein -> 夏筠峥: 我现在才明白你上一条问的是什么意思...就像你上次写的，这个例子中的v相当于δy。所以dv相当于δy'dx。相信你应该理解d(f(x))=f'(x)dx。你这次写的那个分部积分的公式没有错，但是如果想更容易理解，把它写成∫uv'dx=uv-∫vu'dx。这样直接将v=δy带入就可以了。 (10 赞)

成浩然 -> 夏筠峥: 可以证明变分的导数和导数的变分是等价的，这里作者并没有详细写出 (9 赞)

高斌 -> 成浩然: 变分的导数d(derta)=d(y2-y1)=d(y2)-d(y1)=derta(y') (4 赞)

风雨兼程 -> Dr.Stein: 谢谢答主，我这个分部积分一直没搞懂。感觉答主，现在懂了。

电猫哥electricat -> Dr.Stein: 豁然开朗。。。以前每次看到这个分部积分，都感觉莫名其妙，别的书上也没有讲解。这次终于搞明白了，感谢答主！ (1 赞)

新世纪码农战士 -> 成浩然: 一般教材上都没有讲变分的含义讲的特别清楚，更不要说变分的导数和导数的变分了。 (1 赞)

知乎用户bbk2I4:

文中有几个笔误，epsilon->0时，F'->F而非0；另外在推导E-
L公式的时候，完全不需要在外侧在乘以epsilon，完全画蛇添足给读者以误解。泛函在epsilon=0时取得极值，则泛函对epsilon的导数在epsilon=0处等于0即可。在最后导出E-
L公式时，可以对第二项加以说明（给定的任意函数n(x)在边界点x1,x2处相等均等于0），所以第一项等于0，在根据'变分法基本引理‘’推导出E-L=0。根据E-
L可以得到泊松方程。 (8 赞)

狒宝宝的小呆毛 -> 知乎用户bbk2I4: 确实，少乘epsilon后推导简洁了一些

liebealt: 是不是应该是F～趋近于F？ (7 赞)

知乎用户: 清晰~ (3 赞)

Dr.Stein -> TyLIU: 多谢捧场:) (3 赞)

舞步恋曲 -> Dr.Stein: 请教个问题，最简泛函总是说F函数的三个独立变量x，y，y一撇。请问下这个y一撇是y的一阶导数的意思吗？如果是，那它们肯定不属于相互独立的变量了。可是如果y一撇不是y的一阶导数，那为何不写成x，y，y1表示三个变量呢？这样更容易避免和y一阶导数相冲突。这个问题困扰了我很多年了！

人畜无害灰灰猫 -> 舞步恋曲:

y'是一阶导数的意思，关于是不是独立变量可以复习下在多元微积分复合函数下的求导，关于偏导数复合函数的定义
是否存在矛盾？ 知乎上也有这个问题的讨论。

高斌: 吴迪光《变分法》 也不错，比老大中那本好懂些，另外钱伟长先生写的《变分法与有限元》超级多的例子和解答 (5 赞)

快使用双截棍巴拉: 可以推荐下这方面的书吗 (3 赞)

知乎用户n55fm4 -> 快使用双截棍巴拉: 老大中 变分法基础 (8 赞)

快使用双截棍巴拉 -> 知乎用户n55fm4: thanks (2 赞)

夏筠峥:

您讲的很清楚，尤其是很基本的概念有涉及到，我一直没明白变分具体含义是什么，在这里终于解了很多疑惑。有个可能比较基本的问题：
“然后我们可以类比求函数极值时的做法。求函数极值时，我们会令函数的一阶导数为零。”后面的第二个方程式的步骤不是很懂（没有学过偏微分）；
能解释一下拉格朗日方程的物理意义么？而不是纯表达式的推导。 (2 赞)

Dr.Stein -> 夏筠峥:

你好，第二个方程式用到了链式法则(chain
rule)。如果y是a和b的函数，a和b都是x的函数，那么dy/dx=(dy/da)(da/dx)+(dy/db)(db/dx)，形式上看有点类似分数的约分。维百上有例子，看一下应该就理解了。
欧拉拉格朗日方程从数学上的意义来说，就是方程的解是可以让对应原泛函数取得极值的函数。如果赋予F, y,
x不同的物理意义，方程也会有不同的物理意义。我比较熟悉的一个应用是在力学上。https://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E5%8A%9B%E5%AD%A6
可以参看这个维百链接，物理意义是广义牛顿第二定律。 (7 赞)

夏筠峥 -> Dr.Stein:

我感觉我理解的chain rule 是 dy/dx = dy/dz*dz/dx,但是这里是关于dy和dy'两次chain
rule并相加，我感觉相加这里不是很能理解，是对任意的两个variable都可以这样进行chain
rule么，比如y和y’这里是有一定关系的，也可以这样分开求导再相加么。
我查了拉格朗日乘数的推导方式，有用到gradient平行的概念（constrain function和objective
function在极值地方gradient平行），所以我想问的是这个欧拉-拉格朗日方程(E-L equation)是否也能有相关physical
meaning （几何学上的意义）。抱歉可能我问题表述的不是很清楚，还有谢谢您的及时回复！

Dr.Stein -> 夏筠峥:

维百chain
rule里有多元复合函数求导法则https://zh.wikipedia.org/wiki/%E9%93%BE%E5%BC%8F%E6%B3%95%E5%88%99
举个例子，f(x)=x+x^2. 我们可以选择子函数为g(x)=x, h(x)=x^2,
则f=g+h。f'=(df/dg)g'+(df/dh)h'=1+2x。我们也可以选择子函数为g(x)=x, I(x)=(1+x)
,则f=gI。f'=(df/dg)g'+(df/dI)I'=1+x2。是同样的结果，所以子函数的选择不是唯一的，但是要保证所选的子函数能完整的表示出原函数。
不好意思，E-L equation的几何意义我不清楚，帮你at下学理的人试试，@学习ing (1 赞)

KIRA: 写的很清楚，请问F~是怎么得到的？是和F(y~,y'~,x)是同一个函数吗 (1 赞)

十九 -> KIRA: 是一个对应法则，应该是忘记加~了

鱼苔半削: 请问一下，我们书上的拉格朗日-欧拉方程右边是广义力（而不是零），请问这个方程成立是有条件限制的吗？ (1 赞)

致知 -> 鱼苔半削: 保守系 (1 赞)

from: https://api.zhihu.com/articles/20718489