写给物理学家的简明群论(Group Theory in a Nutshell for Physicists by A. Zee)

群论, 物理学, 李代数

【本渣在学习过程中若干处推导笔记已经制作LaTeX排版，生成的pdf文件可在此浏览/下载】。

花了四个半月时间终于死磕完了2022年的第一本书。刚开始看的时候还是春暖花开、万象更新；最后一页合上的时候已是立秋将至。

本书是美籍华裔理论物理学家Anthony Zee（中文名徐一鸿）所著的教材Group Theory for Physicist in a Nutshell. 众所周知，"in a nutshell" 是英语中用来表达浓缩、精华、体积小到可以放进果核里的袖珍书的意思。如果你相信了就输了。这其实是A. Zee和他的出版商（普林斯顿人民出版社）的约定，用来修饰他在该出版社发行的一系列理论物理教材。之前已经出版的是享有盛誉的两本教材Einstein Gravity in a Nutshell （G-Nut)和Quantum Field Theory in a Nutshell (QFT-Nut)。这是他的果核系列第三弹。

可以毫不夸张的说这是迄今为止我看过的最难的一本教材——从四月份开始，我几乎把所有醒着的、非工作的时间都花在这本书的理解和推导上。「塞进果核」绝对只是一个不切实际的描述，全书六百多页、三四斤重，你找个果核试试。

对称性是贯穿整个现代物理学的重要工具，也是全书的主线。本书主要描述了李群（Lie Group）和李代数（Lie Algebra）及其在物理学中的应用。看完之后，对于原来很多科普读物中的关于量子力学、相对论、量子场论、粒子物理和大统一理论的种种语焉不详的描述和比喻都建立了明确的数学既视感，相对完整地串联起了其中的逻辑链条。

自学的过程极其痛苦——消耗草稿纸若干沓，钢笔水半瓶、积累推导笔记LaTeX 3000+行（pdf 35页），octave代码3400+行，golang 700+行，白头发x根，掉头发xx根。但最终完成的那一刻所体会到的认知层次提升带来的无限快感无法描述，之前的痛苦都是值得的。

读者如果对线性代数、微积分有所掌握即可阅读本书，数学前置要求不高。对于物理方面掌握基本的量子力学概念即可，书中涉及的更高级的物理概念（如拉格朗日量密度、量子场等）会有一些背景简介，基本可以做到自给自足。

作者属于话痨型教授，整个果核系列教材都试图营造一种轻松幽默的氛围，穿插一些虚拟人物来从不同角度进行阐述。比如Dr. Feeling会从「直觉」的角度描述一个命题，往往具有更深层的洞见；而Confusio则会时不时提出一些在初学者中常见的迷惑问题；还有一个Jargon Guy会把刚才用日常语言描述的概念定义出一个数学术语。每一章后面或者当页的注脚还会介绍一些名人趣事。不过因为读者在阅读正文的时候并不知道这些注解是无关紧要的故事还是必要的技术性解释，往往打断文气去查阅，结果翻过去一看只是一则八卦，多了不少上下文切换的消耗。

很多地方作者点到为止，留下一些空白由读者来填充。也许是我太驽钝了，这些空白经常会给我造成几天的停滞，很痛苦的搞通了之后的确加深了理解。作为初学者，后知后觉的了解到作者用同样的字体SU(2)代表李群和李代数并不是标准做法——通常李代数使用不同的字体 代表。如果作者也采用这一通用做法，也许我对李群和李代数的混淆也会早些澄清。

本书共分九章。

正式章节开始之前有一个线性代数的回顾性章节，涉及到的都是线性代数的最基本的常识。其中用ε符号表达的NxN矩阵行列式的通用公式是后面经常用到的，并且是一般大学线性代数里不常涉及到的，值得注意。

• 第一章：从对称性引入「群」的基本概念和定理，从离散群过渡到连续群，再到无限小生成元（generator）和李代数的概念。
• 第二章：定义群的矩阵表示，多次默念Character is function of Class这句「经文」，舒尔引理（Schur's Lemma）和正交关系，如何构建一个有限群的特征标表（Character Table）。
• 第三章：对量子力学、哈密尔顿量和拉格朗日量做一个简要回顾，并举例说明如何通过对称性和群论来找到谐振系统的特征模式。
• 第四章：重点章节，十分详尽地不厌其烦地从各个角度把旋转群及其代数SO(N)盘了个底掉。
  • 其中引入了重要的「张量」的概念，以及如何利用张量构建SO(N)的高维矩阵表示。不得不说，当得知三维旋转群有五维、七维不可约矩阵表示的时候，我的内心是崩溃的。
  • 从SO(N)过渡到SU(N)，解释由于复数共轭的关系引入张量「上标」和「下标」的区别。
  • 这里面反复做的游戏就是如何把张量重新线性组合从而将「可约表示」分解为「不可约表示」（Irreducible Representations）的直和。而之所以如此强调「不可约表示」是因为它是整个现代粒子物理和大统一理论的基本语言，一定要吃透（见下文第九章内容）。
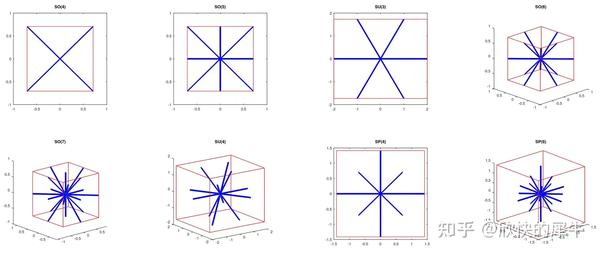
  • SU(2)是SO(3)的双重覆盖（Double covering group)，连续李群的测度、积分、流形，几个常见李群的流形拓扑结构。（代数和几何在这里连接在一起，也让我的逻辑链条着实又完整了一环）。
  • 
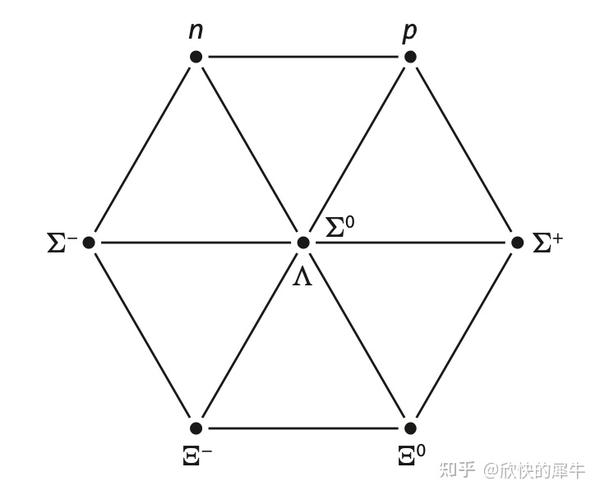
• 第五章：主要介绍之前的SU(2)和SU(3)是如何在最近几十年应用于粒子物理领域。原来意义上的对称性诸如SO(3)是指物理系统的时空对称性，而粒子物理中存在一个巨大的内部空间对称性符合SU(2)和SU(3)。「粒子是不可约表示」成为中心思想。Gell-Mann矩阵和夸克模型（Eightfold way of SU(3)，见上图）。虽然单靠群论无法获得物理系统的精确解，但是通过群及其体现出来的对称性可以给到解空间的限制条件。
  • 
• 第六章：李代数的根系（Root system）、权（Weight）和李代数的完全分类。李代数的Dynkin图表示，所有的李代数可以划分为有限的几类。
• 第七章：很庞杂也很难的一章：
  • 首先将视野放回SO群，通过Clifford Algebra构建出2^n维「旋量」（Spinor）表示。
  • 摆脱以往紧致李群（Compact Lie Group）的限制，开始讨论洛伦兹群及其阐述的相对论不变性。洛伦兹群SO(3,1)是旋转群SO(4)的解析延拓（Analytic Continuation）。闵可夫斯基空间是欧几里得空间的广义扩展。这几章加强了之前在电磁学中关于电场和磁场混合构成洛伦兹协变张量的思想。
  • 洛伦兹代数通过添加「平移变换」扩展为庞加莱代数。
  • 通过Spinor表示构建出的拉格朗日量符合Weyl方程，这是通过群论（加物理直觉的组合）可以直接得到的方程。而Weyl方程因不符合宇称守恒而被狄拉克方程所取代，但后来宇称守恒被打破才发现Weyl方程是更基础的描述语言。
  • 通过Weyl方程推导出狄拉克方程的一章非常赞，从简化的静止坐标系通过洛伦兹不变性得到任意坐标系的狄拉克方程，赞赞赞！
  • 狄拉克方程的共轭解对应反物质，反物质实际上是Spinor的「赝实」Pseudoreal表示（多妙的翻译）。
  • 从狄拉克方程再鼓捣出一个拉格朗日量得到了Majarana方程，可以描述单一手性、无电荷、有质量的粒子，为中微子度身定做（狄拉克方程无法描述单一手性粒子）。
• 第八章：李代数可以缩减和扩展。从洛伦兹代数扩展为共形代数（Conformal Algebra），指数增长的宇宙膨胀可以通过陪集流形（Coset Manifold）SO(4,1)/SO(3,1) 来解释。
• 第九章：全书点睛之笔，从群论的角度来阐述规范场论和大统一理论的核心思想：
  • 费米子是李代数的「不可约表示」，规范玻色子是李代数的生成元（generator）。
  • 玻色-费米耦合按照李代数生成元的定义进行，玻色子彼此之间的交互通过伴随表示（Adjoint Representation）定义。
  • SU(3)定义强相互作用，SU(2)定义弱相互作用，SU(3)⊗SU(2)⊗U(1)联合起来描述强+弱+电磁作用，得到统一！
  • 更近一步，从审美角度，从SU(3)⊗SU(2)⊗U(1)寻找单一李代数来进行「大统一」，找到SU(5)，粒子表示为5⊕10。更大的代数意味着更多可能的粒子反应，由此预言质子衰变。
  • 再进一步试图将粒子的5⊕10表示变成更大的不可约表示，从SU(5)理论到SO(10)理论的扩展！

真的很难想象靠着这样一本书可以从最初等的对称性一直攀缘到大统一理论的基本原理。这个过程凝聚着无数天才科学家的奇思妙想，但每个人都有一个坚定的信仰，就是自然所依靠运行的法则必定是美的。这是一个很难科学定义的标准，只能说是科学家们的一厢情愿。然而，正像作者在书中无数次慨叹过的"Nature is kind to humans"，大自然所体现出来的法则和其背后的数学原理无时无刻不在为人类加持着这一信仰。

不变的执着: 您好，感谢您的分享，请问我点进github之后，点哪个按钮才能下载pdf呢？

欣快的犀牛 -> 不变的执着: 你好，直接克隆整个代码库到本地即可。或者点“view code”一个个下载也行[大笑]

知乎用户: 这本书我看过2遍，可以说非常不适合自学。它的风格是你看完后感觉非常爽，但是缺乏很多formal的定义和例题/习题推导，会让你感觉事后倍感空虚。Zee书往往只有鲜明的物理图像而数学细节没有扎实的锻炼，最后都是这种效果。他的场论也有这个缺点，所以才没成为多数人的场论首选教材。

from: https://api.zhihu.com/articles/548760884