
title: 李群是什么——几何与代数的结合
permalink: https://zhuanlan.zhihu.com/p/662576340
author: 斯宾王
author_id: 79a8daad1fdb575ebd245d61fe6a5ea0
column: 代数学习笔记
column_id: c_1500047808242061312
voteup: 313 赞同
created: 2024-01-02T18:03:38
updated: 2024-01-02T18:03:38
fetched: 2024-06-26T13:37:16
count: 约 45713 字
version:
tags: [群论, 微分几何, 李群与李代数, 斯宾王, 代数学习笔记]
url: https://zhuanlan.zhihu.com/p/662576340

李群是什么——几何与代数的结合

from 专栏代数学习笔记

话题:

群论, 微分几何, 李群与李代数, 斯宾王, 代数学习笔记

正文:

李群（Lie group）是一个群，同时也是一个光滑流形（smooth manifold）。一个流形在局部和一个欧几里得空间（Euclidean space）类似，而一个群是一个是一个集合和一个二元运算（binary operation）组成的抽象机构，其中二元运算满足一些特定运算规律。将这个几何结构和这个代数结构结合起来，我们可以得到一个连续群（continuous group），其中点的相乘和取逆是连续的。如果点的相乘和取逆还是光滑的，那么我们就得到一个李群。在介绍李群的概念之前，我们首先要引入光滑流形的概念。

1 光滑流形

1.1 欧几里得空间中的光滑曲面

首先，我们要给出导数（derivative）和偏导数（partial derivative）的定义。

定义 1.1 令为一个开集，并令 . 对于一个函数，若存在一个线性映射（linear map），使得则称在处是可导的（differentiable）. 线性映射叫作在处的导数，写作 . 对于和，在处关于的偏导数被定义为这时此极限存在.

我们需要利用偏导数对“光滑”进行定义。

定义 1.2 令为一个开集，并令 . 对于一个函数，若其所有长度小于等于的偏导数都是连续函数，则称 . 若对于所有，都有，则称是光滑的，写作 .

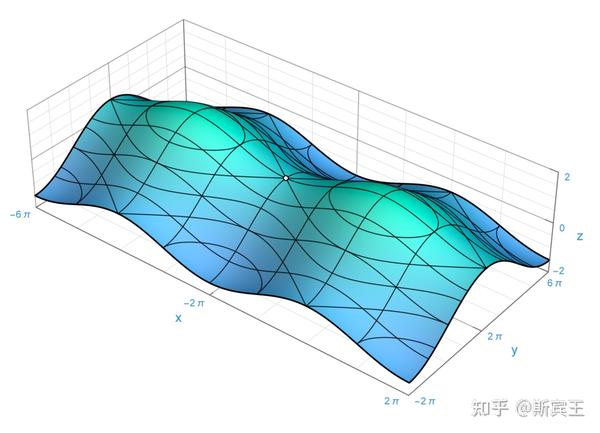一个光滑流形就是一个对光滑曲面（smooth surface）的一般化。一种最基础的光滑曲面就是一个光滑函数的图像。也就是说，若是一个光滑函数，则它的图像是一个光滑曲面。考虑相关函数，它由给出。根据定义，是和之间的一个双射（bijection）。事实上，它是一个同胚（homeomorphism）。集合是的一个拓扑子空间（topological subspace），而且是一个从到的连续双射，它的逆也是连续的。因此，曲面和开集在拓扑意义上是相同的。不是所有曲面在整体都是一个函数的图像。

一个三维空间中的曲面

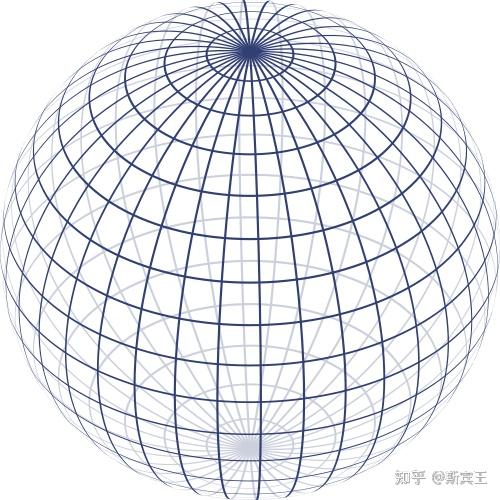例 1.3（球面） 令为一个 -单位球面. 它不是一个将任一变量用其他个变量表示的函数图像，因为对于任意满足的标量，坐标线经过上的两点. 事实上，是函数在高度上的水平集（level set）. 由于对于任意都不为，所以它对于任意都是满秩的（of full rank）. 因此，对于任意，我们都可以找到某些坐标使得 . 根据隐函数定理（implicit function theorem），存在一个光滑的局部函数，使得在附近，是的图像. 因此，尽管在整体不是一个光滑函数的图像，它在局部仍是一个光滑函数的图像.

一个三维球面

我们现在给出光滑曲面的定义。

定义 1.4 令为正整数. 一个在中的光滑 -维曲面是一个满足如下性质的集合：对于任意，都有一个开集和一个光滑函数，以及某些对坐标的分割和，这里，使得对于和，当且仅当 . 也就是说，一个在中的光滑 -维曲面是一个在局部是个变量作为其他个变量的函数的图像的一个的子集.

接下来，我们给出正则值（regular value）的概念。

定义 1.5 令为一个光滑函数. 对于，若对于任何水平集中的点，导数都有满秩，则称是的一个正则值.

与正则值相联的水平集是一个光滑曲面。

命题 1.6 若为一个光滑函数，且是的一个正则值，则水平集是一个在中的光滑 -维曲面.

证明在矩阵中选取个枢轴列（pivotal columns），那么由这些列组成的子矩阵是可逆的（invertible）. 根据隐函数定理，水平集在局部是这个变量作为其他个变量的函数的图像.

由正交矩阵构成的正交群（orthogonal group）是一个光滑曲面的例子。

例 1.7（正交群） 正交群由满足的实矩阵组成，这里的列构成了的一个标准正交基底（orthonormal basis）. 由于，，所以里的行也构成了的一个标准正交基底. 在矩阵乘法下是一个群. 注意，若，且，则，所以包含了的所有线性等距（linear isometry）. 事实上，它是的所有线性等距的群.

根据定义，是水平集，这里，且是一个光滑函数，这里是一个由实矩阵构成的 -维向量空间（vector space）. 事实上，我们可以将的陪域（codomain）视作由自伴（self-adjoint）矩阵，即对称矩阵构成的集合，因为 . 的维度是 . 现在，我们计算的导数. 对于任意，是一个由给出的线性映射. 对于，若是一个对称矩阵，取，有因此，是满射的（surjective），即满秩的. 那么，是的一个正则值. 根据命题1.6，是一个在中的光滑曲面，其维度是 .

1.2 拓扑流形

一个光滑流形就是一个对光滑曲面的一般化。事实上，每个 -维光滑流形都是中的某个光滑曲面，这里。在介绍光滑流形之前，我们需要引入拓扑流形（topological manifold）的概念。

定义 1.8 一个 -维流形是一个局部欧几里得的、第二可数的（second-countable）豪斯多夫空间（Hausdorff space）. 具体来说，是

局部欧几里得的：对于，存在一个的开邻域（neighborhood），它和中的一个开集是同胚的. 令为中这样的一个开集，并令为一个同胚，那么叫作临近的一个坐标卡（coordinate chart）.
第二可数的：存在一个中的开集的可数族，使得中的任一开集都是中的集合的并集.
豪斯多夫的：对于两个不同的点，存在两个开集，使得，，且 .

第二可数性条件可以排除一些奇怪的拓扑空间，它们“太大”，以至于不能成为流形。豪斯多夫条件可以排除一些病态的拓扑空间，比如有两个原点的实直线。流形的定义的核心是，它要在局部是欧几里得的。下面的命题指出，光滑曲面是流形。

克莱因瓶是一个流形

命题 1.9 若是中的一个 -维光滑曲面，则是一个 -维流形.

证明由于是第二可数的且豪斯多夫的，作为的一个子集，也是第二可数的且豪斯多夫的. 根据定义，对于任意，存在坐标分割，其中，，和一个开集，以及一个光滑函数，使得图像在靠近处和重合. 函数是到其像上的一个同胚. 那么，是在中的一个的开邻域，同胚为 .

一个 -球面是一个 -维流形。

例 1.10（球面） 由于一个 -单位球面是一个光滑曲面，根据命题1.9，它是一个 -维流形. 对于，定义开半空间为并定义为北半球和南半球. 不难验证，是函数的图像，这里是光滑函数，其中是一个 -单位球（ball）. 任意点被包含在至少一个半球中. 因此，靠近中一点的坐标卡是，其中同胚由给出. 它的逆是，这里被放置在第个坐标中.

在下面的例子中，流形不是一个欧几里得空间的子集。

例 1.11（实射影空间） 实射影空间（real projective space）被定义为的所有 -维子空间的集合，即中的元素是在中经过原点的直线. 实射影空间通过商映射（quotient map）被定义为一个拓扑空间. 这意味着在中是开集当且仅当在中是开集. 它也可以被视作具有等价性关系的 -球面的商空间（quotient space）. 此外，是第二可数的且豪斯多夫的.

对于，令为满足的点的集合，并令 . 那么，就是不和平面平行的的 -维子空间的集合. 由于是开集，是开集. 由于没有和所有坐标平面都平行的的 -维子空间，中的每一点都被包含在至少一个中.

定义为此映射是良定的，因为对于任意标量，有 . 由于是连续的，是连续的. 事实上，它是一个同胚，它的逆是连续的. 因此，是局部欧几里得的，所以是一个 -维流形.

三维欧几里得空间中的实射影平面

最后一个例子是积流形（product manifold）。

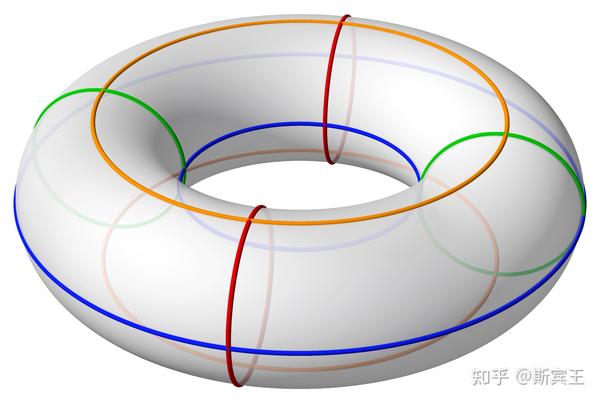例 1.12（积流形） 令为维度分别是的流形，那么是一个维度是的流形. 有限或可数多个第二可数豪斯多夫空间的积是一个第二可数豪斯多夫空间. 对于局部欧几里得性质，若，在每个附近选择一个坐标卡，则是附近的一个坐标卡. 特别地，一个 -环面是个圆（circle）的积，它是一个 -维流形.

一个三维环面

1.3 光滑流形

我们希望一个光滑流形的坐标卡中的同胚是一个光滑函数，但是一般来讲这没有意义。由于一个流形是一个抽象的拓扑空间，我们不知道如何定义一个函数的光滑性。现在，我们先要给出一个光滑函数的定义。我们将采取局部定义：给定和附近的一个卡，复合函数是光滑的。附近会有不止一个卡，而我们对光滑性的定义不应取决于对坐标卡的选择。我们需要一个无矛盾性条件来确保定义的良定性。

定义 1.13 令为一个流形，并令和为两个卡，这里 . 从到的转移映射（transition map）是复合映射这里和是的两个开子集，而是它们之间的一个同胚. 若转移映射是一个微分同胚（diffeomorphism），即一个逆映射为可导映射的可导双射，则这两个卡被称作光滑相容的（smoothly compatible）. 一个定义域覆盖全部的卡的族叫作的一个图册（atlas）. 若中所有的卡都是光滑相容的，则称是一个光滑图册.

例 1.14（接例 1.10） 在的情况下，考虑两个卡和，这里是圆在第一象限的部分. 由于，，那么从到的转移映射是这是一个单位区间上的光滑映射. 事实上，它是一个微分同胚. 类似地，我们可以证明中的转移映射都是微分同胚，所以它是一个上的光滑图册.

例 1.15（接例 1.11） 考虑上的图册 . 若，则是一个从到的光滑映射. 事实上，它是一个微分同胚. 因此，是上的一个光滑图册.

例 1.16（接例 1.12） 给定上的光滑图册，它们的积是上的一个光滑图册.

我们想要用光滑图册定义光滑流形，但有两个原因导致我们还不能这样做。第一，一个流形有可能有多个光滑图册，且它们互相之间不是光滑相容的。这样，不同的光滑图册对于同一个流形会给出不同的光滑流形的定义。第二，两个不同的光滑图册可能给出一个相同的光滑函数类，这时我们不希望这两个不同的流形-图册对给定义出不同的光滑流形。现在，我们正式给出光滑流形的定义。

定义 1.17 令为一个流形. 若的一个光滑图册不是其他光滑图册的真子集，则称是完全的（complete）或最大的（maximal）. 也就是说，若任何卡和中的所有卡都是光滑相容的，则称是完全的. 上的一个完全的光滑图册叫作上的一个光滑结构（smooth structure）. 一个光滑流形是一个对，其中是一个流形，是上的一个光滑结构.

此定义的一个缺点是：一个完全的光滑图册非常大，故不容易描述。下面的结论对这个问题进行了解决。

引理 1.18 令为一个流形，并令为上的一个光滑图册. 那么，在上存在唯一的一个光滑结构使得，这里叫作由决定的光滑结构.

证明定义为和中所有的卡都光滑相容的所有卡的集合. 由于是一个光滑图册，，且是一个图册. 我们需要证明三点：

是一个光滑图册，即其中的所有卡都是光滑相容的.
是一个光滑结构，即它是一个完全的光滑图册.
是唯一的包含的光滑结构.

为了证明第一点，令和为中的两个卡，这里 . 我们需要证明是一个微分同胚. 由于我们要考虑所有卡对，包括这两个卡反过来的情况，所以我们只需证明在上是光滑的. 令，并令 . 由于是一个图册，它包含某个卡，使得 . 根据定义，和都与是光滑相容的，故和在各自定义域上都是光滑的. 那么，在的一个邻域中，是光滑的. 由于是任意的，在上是光滑的. 因此，是一个光滑图册.

第二点容易证明. 由于，若是一个和中所有的卡都光滑相容的卡，它就和中所有的卡光滑相容. 根据定义， .

为了证明第三点，令为任一包含的光滑结构. 由于是一个光滑图册，其中每个卡都和中所有的卡光滑相容. 根据定义， . 由于是完全的，且中所有的卡都是光滑相容的， .

下面的例子介绍了欧几里得空间作为一个光滑流形，其上的光滑结构。

例1.19（欧几里得空间） 欧几里得空间有一个标准的光滑结构，它由单坐标卡决定. 然而，还有其他不同的光滑结构. 例如，当时，考虑卡，这里，它是一个从到的同胚. 根据引理1.18，上存在一个包含这个卡的光滑结构. 它不是标准光滑结构，否则和应该是光滑相容的. 然而，是映射，它不是光滑的.

下面是其他光滑流形的例子。

例 1.20（可逆矩阵群） 令为一个光滑流形，它有完全的光滑图册 . 若是一个开集，则也是一个光滑流形，它的光滑结构由决定. 这是因为，由于是完全的，它的被包含的卡包括一个对的覆盖，所以是一个图册. 特别地，的每个开子集都是一个光滑流形.

可逆矩阵群是一个李群. 由于它可以被描述. 由于是连续的，且是一个开集，是的一个开子集. 因此，是一个光滑流形. 事实上，是的一个开稠密（dense）子集. 为了证明这一点，令为一个矩阵，并令为它的特征多项式（characteristic polynomial）. 这个多项式有个复根，它们是的特征值（eigenvalue）. 令 . 对于，是可逆的，故在中是稠密的.

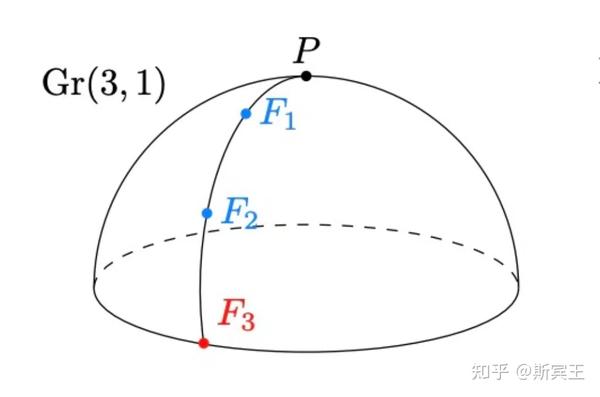例1.21（格拉斯曼流形） 格拉斯曼流形（Grassmannian manifold）是实射影空间的一般化. 对于，令为的 -维子空间的集合. 因此，实射影空间是的一个特例，即 . 同构在上定义一个标准光滑结构，可以将其视作一个光滑流形.

格拉斯曼流形Gr(3,1)

2 子流形

为了进一步阐释光滑流形的概念，我们要对子流形（submanifold）进行介绍。考虑一个线性映射。为了计算两个子空间和的维度（dimension），我们只需知道的秩（rank）。根据定义，。根据线性代数基本定理（fundamental theorem of linear algebra），。

令为两个流形之间的一个光滑映射。我们想要理解集合，以及对于所有，集合。由于是光滑的，它应该可以被它的微分（differential）很好地建模。此微分在每一点都是一个线性映射，这里是的切空间（tangent space）。切空间和微分的具体定义如下。给定，点对的切空间被定义为。

定义 2.1 令为一个光滑流形，并令 . 在处的求导空间（space of derivations）是一个由线性算子（linear operator）构成的空间，其中满足
若，则映射是一个向量空间（vector space）之间的同构（isomorphism）。事实上，一个光滑流形的切空间被定义为在处的求导空间。接下来，我们给出欧几里得空间之间的光滑映射的微分的定义。

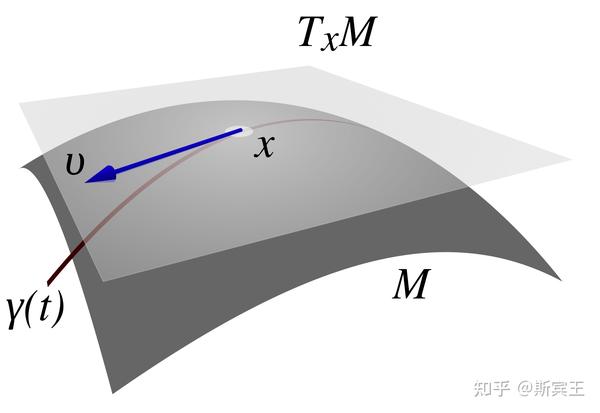切空间

定义 2.2 若为一个光滑映射，则在处的微分被定义为
可以证明，微分映射可被给出。我们可以根据此结论给出光滑流形之间的光滑映射的微分的定义。

定义 2.3 令为光滑流形，并令为一个光滑映射. 对于，微分由给出.

注意，若，则满足因此，，故是良定的。

下面的例子告诉我们，如果我们想要的像（image）和水平集（level set）有好的表现，我们需要不随变化。

例 2.4 令映射为 . 那么，不是一个流形，且水平集对于是空集. 对于，水平集是圆，是 -维流形. 对于，水平集是一个 -维流形. 导数是一个线性映射. 对于，它的秩是；对于，它的秩是 .

2.1 常秩映射

令为流形之间的一个光滑映射。在每个点，微分是一个线性映射。它的秩是它的像的维度。若对于所有点，的维度都是一个常值整数，则称有常秩，写作。根据线性代数的结论，。若和上界相等，则称在处是满秩的（full rank）；若这对于所有点都成立，则称是满秩的。

对于一个线性映射，若它的秩和陪域的维度相等，则称它是满射的；若它的秩和定义域的维度相等，则称它是单射的。这两种情况对常秩光滑映射非常重要。

定义 2.5 令为一个常秩光滑映射. 若，则称是一个浸入（immersion），这时对于所有都是单射的. 若，则称是一个浸没（submersion），这时对于所有都是满射的.

事实上，这两个条件在局部也是有意义的（一个邻域上的浸入或浸没），这时它们是开条件。

引理 2.6 令为一个常值光滑映射，并令 . 若是单射的，则存在一个的邻域使得是一个浸入. 若是满射的，则存在一个的邻域使得是一个浸没.

证明对于一个附近的卡（chart）和一个附近的卡，有坐标表示这时可被雅可比矩阵（Jacobian matrix）表示，这里 . 令为的秩. 若是单射的，则，故中有个线性独立的（linearly independent）行. 通过对坐标进行重新排序，我们可以假设的上子矩阵是可逆的. 可逆性是一个开条件，且在卡中的分量函数是连续的，所以这个子矩阵在的一个邻域中是可逆的. 那么，，故在上是一个浸入. 类似地，我们也可以证明是一个局部浸没.

下面是一些浸入和浸没的例子。

例 2.7（1）（射影映射） 若是光滑流形，则射影映射（projection map）是浸没. 特别地，映射是一个从到的浸没.

（2）（光滑曲线） 若在中且是一个光滑曲线，则是一个浸入当且仅当，这里
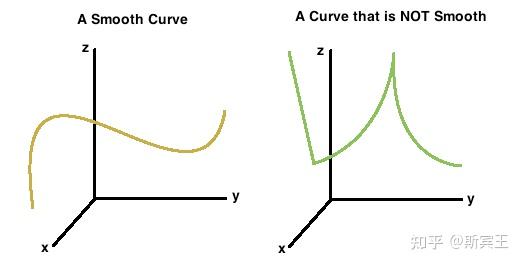光滑曲线和非光滑曲线

（3）（束射影） 束射影（bundle projection）总是一个浸没.

若一个映射既是一个浸入又是一个浸没，它不一定是一个微分同胚，但它一定是一个局部微分同胚（local diffeomorphism），这就是流形的反函数定理（inverse function theorem）所说的内容。

定理 2.8（流形的反函数定理） 令为一个光滑映射，并令 . 若是可逆的，则存在连通邻域和，使得是一个微分同胚.

证明由于是可逆的，和的维度相等，所以和的维度相等. 选择在处的卡和在处的卡 . 在这些坐标中，令，并令 . 根据假设，是可逆的. 根据普通的反函数定理，存在连通邻域和，使得是一个微分同胚. 取和，证毕.

一个既是浸入又是浸没的映射（其微分在每一点都是可逆的）叫作一个局部微分同胚。下面的结论在某种意义上是反函数定理的反向陈述。

引理 2.9 令为一个常值光滑映射. 假设对于所有点，都存在一个的邻域，使得是一个到其像上的微分同胚. 那么，既是一个浸入又是一个浸没.

下面是局部微分同胚的一些性质。

命题 2.10 局部微分同胚的性质包括：

（1）局部微分同胚的复合是局部微分同胚；

（2）局部微分同胚的一个有限笛卡尔积（Cartesian product）是一个局部微分同胚；

（3）局部微分同胚是开映射；

（4）一个局部微分同胚在一个开集上的限制是一个局部微分同胚；

（5）微分同胚是局部微分同胚；

（6）一个双射局部微分同胚是一个微分同胚.

对于常秩映射的最重要的局部定理是秩定理（rank theorem）。

定理 2.11（秩定理） 令为光滑流形，这里且，并令为一个有常秩的光滑映射. 对于每个点，都有在处的卡和在处的卡，这里，使得有坐标表示
由于这是一个局部定理，它是一个关于欧几里得空间的开子流形之间的光滑映射的陈述。对它的证明和对普通隐函数定理（implicit function theorem）的证明类似。

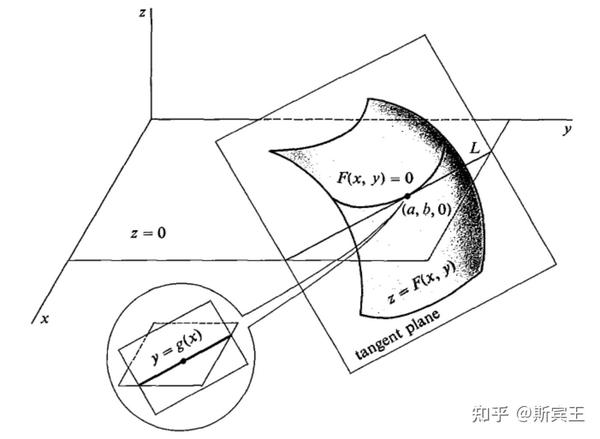隐函数定理

特别地，此定理有两个特殊情况：

若是一个浸入，则，且 .
若是一个浸没，则，且 .

这些表示的最重要的性质是：它们是线性函数。

推论 2.12 令为连通的，并令为一个光滑映射. 那么，下面的陈述是等价的：

（1）有常秩序.

（2）对于每个点，都有在处和在处的卡，使得在这些局部坐标中，是线性的.

证明秩序定理表明 . 假设（2）成立. 由于任意线性映射都有常秩，且在一点的坐标表示的导数的秩和微分的秩相等，在每个卡上都有常秩. 根据连通性，得到有常秩.

下面是秩定理的全局版本。

定理 2.13（全局秩定理） 令为光滑流形，这里且，并令为一个有常秩的光滑映射. 那么，

（1）若是单射的，则它是一个浸入；

（2）若是满射的，则它是一个浸没；

（3）若是双射的，则它是一个微分同胚.

证明对于（1），假设不是一个浸入，即 . 固定 . 根据秩定理，我们可以选取在处的卡和在处的卡，这里，使得在这些坐标中 . 特别地，对于足够小的，，这里在之前有个 . 这样，就不是一个单射，因而也不是.

对于（2），假设不是一个浸没，即 . 根据秩定理，在每个点，我们可以选取在处的卡和在处的卡，这里，使得在这些坐标中 . 通过在必要时缩小坐标邻域，我们可以假设是紧的，且 . 那么，是的一个紧子集. 这是的一个闭子集，且它自身没有开子集，所以在中是无处稠密的（nowhere dense），即 . 从卡中选取的一个可数覆盖 . 那么，对于每个，是闭的和在中无处稠密的. 因此，是一个无处稠密的集合的可数并集. 根据贝尔类型定理（Baire category theorem），在中是稠密的，所以，即不是一个满射.

对于（3），由于是双射的，根据（1）和（2），既是一个浸入又是一个浸没，因而是一个局部微分同胚. 根据命题2.10（6），是一个微分同胚.

2.2 浸入与嵌入

一个单射浸入是一个流形版本的单射线性映射，而且构成了定义子流形的框架。然而，下面两个例子表明，这个概念有一些问题。

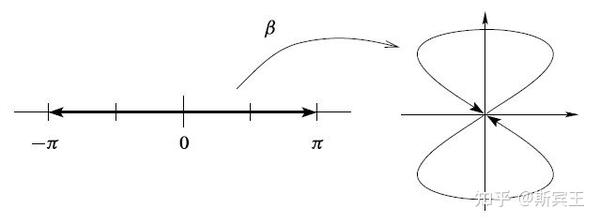例 2.14 令为曲线这是对一个双纽线（lemniscate）的参数化. 它是的解集. 根据公式，我们可以验证，是单射的. 它还是一个浸入，因为，其中第二个坐标在定义域中只在为，而在这两点第一个坐标为，因而 . 然而，的像是双纽线，它不是一个流形. 原点没有局部欧几里得的邻域. 此外，若我们将的像赋予子空间拓扑，则不是一个同胚，因为像是紧的（compact），而定义域不是. 因此，是一个单射浸入，但不是一个拓扑嵌入（在子空间拓扑中到其像上的同胚）.

一个不是拓扑嵌入的单射浸入

例 2.15 令为环面，并定义曲线为这里是一个无理数. 此映射是单射的，也是一个浸入，两个坐标都不在任意为 . 然而，像在中是稠密的（dense），所以不是一个拓扑嵌入.

为了避免这种情况，我们将焦点放在是拓扑嵌入的单射浸入。

定义 2.16 令为光滑流形. 对于一个映射，若是一个拓扑嵌入，还是一个浸入，则称是一个光滑嵌入.

一个光滑的拓扑嵌入也不一定是一个光滑嵌入。

例 2.17 令为映射 . 它是一个像为的单射映射，也是一个到其像上的同胚. 它还是一个光滑映射. 然而，由于，它不是一个到其像上的微分同胚，因而不是一个浸入.

下面是一些光滑嵌入的例子。

例 2.18（1） 若是一个光滑流形，且是一个开集，那么包含（inclusion）是一个光滑嵌入.

（2） 令为光滑流形，并令为其中的点. 对于每个，若映射被定义为则是一个光滑嵌入. 特别地，若取，，，，则的嵌入是一个光滑嵌入.

（3） 若被定义为则是一个光滑嵌入.

有一些条件可以保证一个单射浸入是一个嵌入。

命题 2.19 令为光滑流形，并令为一个单射浸入. 若下面四个条件中的任意一个成立，则是一个光滑嵌入：

（1）是一个开映射或闭映射；

（2）是一个恰当映射（proper map），即一个紧集在下的前像（preimage）是紧的；

（3）是紧的；

（4） .

证明首先，注意 . 若是紧的，则中的任意闭集在连续映射下的前像是紧的. 若是一个局部紧豪斯多夫空间（locally compact Hausdorff space）间的恰当映射，则它是一个闭映射. 那么，我们只需证明（1）可以推出是一个嵌入. 由于一个连续的且单射的开映射或闭映射总是一个嵌入，我们证明了（1），（2），（3）可以推出是一个嵌入.

现在，我们证明（4）可以推出是一个嵌入. 由于是一个浸入，在任意处都是单射的. 由于的定义域和陪域的维度相等，是一个双射，所以是一个单射的局部微分同胚. 根据命题2.10（3），是一个开映射. 由于一个连续的且单射的开映射是一个嵌入，我们证明了（4）可以推出是一个嵌入.

例 2.20（包含映射） 令为包含映射（inclusion map）. 此映射是光滑的，还是一个浸入，因而是一个单射浸入. 由于是紧的，根据命题2.19（3），是一个光滑嵌入.

例2.14和例2.15是两个单射浸入不是光滑嵌入的例子，但在这些例子中，这些映射是局部光滑嵌入，即定义域中的每一点都有一邻域使得映射在其上是一个光滑嵌入。

定理 2.21 令为光滑流形，并令为一个光滑映射. 那么，是一个浸入当且仅当中的每一点都有一邻域使得是一个光滑嵌入.

证明假设每一点都有这样一个邻域. 那么，对于任意，是满秩的，所以是一个浸入. 假设是一个浸入，并令 . 根据秩定理，存在一个坐标卡，使得在局部坐标中，有的形式. 那么，是一个单射. 选取一个开子集使得是紧的且 . 那么，是一个紧集上的单射连续映射. 根据命题2.19（3），是一个光滑嵌入. 因此，是一个光滑嵌入.

2.3 子流形

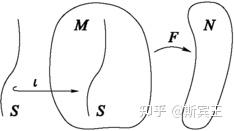一个流形的一个嵌入子流形（embedded submanifold）是一个在子集拓扑中的拓扑流形，它有一个光滑结构（smooth structure），使得包含映射是一个光滑嵌入。嵌入子流形有时也被称作正则子流形（regular submanifold）。若是的一个嵌入子流形，则称为一个周围流形（ambient manifold）。的余维度（codimension）是。根据定义，一个嵌入子流形是一个光滑嵌入（到嵌入子流形的周围流形的包含映射）的像。反向的陈述仍成立。

嵌入子流形

命题 2.22 令为一个流形之间的光滑嵌入，并令 . 那么，是一个在子空间拓扑中的拓扑流形，且上存在一个唯一的光滑结构，使得是一个嵌入子流形，且上一个到上的微分同胚.

证明由于是一个光滑嵌入，它是一个拓扑嵌入，故它是一个从到的同胚. 那么，是一个在子空间拓扑中的拓扑流形. 对于任意上的卡，定义上的卡的形式为 . -平移映射和 -平移映射相同，所以它们构成一个图册. 此光滑结构使成为一个微分同胚，它由在局部坐标中的单位映射给出，且这样的光滑结构显然是唯一的. 包含映射由给出. 由于它是一个光滑嵌入和一个微分同胚的复合，它是一个光滑嵌入，所以是一个嵌入子流形.

因此，一个嵌入子流形正是某光滑嵌入的像。光滑嵌入也叫作（全局）参数化（parametrization）：我们通过某些其他内在流形对进行参数化。最简单的嵌入子流形是开子集，它们是仅有的余维度为的嵌入子流形。

命题 2.23 一个子集是一个余维度为的嵌入子流形当且仅当在中是开的.

证明假设是开的. 在局部坐标中，包含映射由单位映射给出，所以它是一个单射浸入. 由于它还是一个拓扑嵌入，是一个嵌入子流形. 由于和的维度相等，的余维度是 .

假设是一个余维度是的嵌入子流形. 那么，包含映射是一个浸入. 由于，且在每个处都是单射的，它在每个处也是满射的. 因此，是一个局部微分同胚. 根据命题2.10（3），是一个开映射. 因此，在中是开的.

下面是一些嵌入子流形的例子。

例 2.24 令为光滑流形. 对于任意，是一个嵌入子流形. 是的像. 是一个光滑嵌入.

例 2.25（图像） 令为光滑流形，并令为一个开集. 令为一个光滑映射，则图像是一个嵌入子流形. 它的维度是，余维度是 . ，这里是映射，它是一个光滑映射. 若是射影映射，则 . 根据链式法则，有由于这个复合映射是单射的，是单射的，所以是i 一个浸入. 它还是一个拓扑嵌入，它的逆是 . 因此，是一个和微分同胚的嵌入子流形.

特别地，的任意仿射子空间（affine subspace）都是一个嵌入子流形，因为它是一个仿射函数的图像。最简单的例子是常规的嵌入，它由给出。事实上，这是对任意余维度为的嵌入子流形的局部模型。

令为一个光滑 -流形，并令为中的一个局部卡。一个的 -切片（ -slice）是一个子集，它满足这里常数。对于一个子集，若对于所有，都有一个在处的卡使得是一个 -切片，则称满足局部 -切片条件。

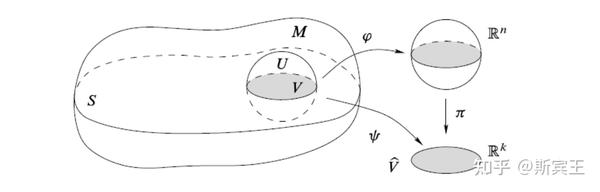一个满足k-切片条件的子集S

定理 2.26（切片定理） 令为一个光滑流形，并令 . 若为一个 -维嵌入子流形，则它满足局部 -切片条件. 若为一个满足局部 -切片条件的子集，则它是一个在子空间拓扑中的 -维拓扑流形，且有一个唯一的光滑结构使得它称成为一个嵌入子流形.

证明若是一个嵌入子流形，则包含映射是一个浸入. 根据秩定理，对于每个，都有在处的卡和在处的卡，使得在局部坐标中 . 通过在必要时缩小邻域，我们可以假设，这样就满足局部 -切片条件.

若为一个满足局部 -切片条件的子集，则我们可以用局部切片卡构造一个的图册，并将其与从到的射影复合.

最有用的一种嵌入子流形是可被视作水平集的那种。若是一个函数，且，则的 -水平集是。可以证明，的任意闭子集都是某光滑函数的一个水平集。因此，我们需要对进行严格的限制，以确保水平集是嵌入子流形。一个简单的条件是有常秩。

命题 2.27 令为一个有常秩的光滑函数. 那么，对于任意点，水平集是一个余维度为的嵌入子流形.

证明令，并固定 . 根据秩定理，有在处的卡和在处的卡，使得，这里 . 那么，在这些坐标中，，这里是常数，故是切片因此，满足局部 -切片条件. 根据切片定理（slice theorem），是一个维度为的嵌入子流形，因而它的余维度是 .

推论 2.28 若为一个浸没，则的每个水平集都是一个在中的余维度为的嵌入子流形.

在满秩的特殊情况中，没有必要在每处都是一个浸没. 它在水平的一个邻域中是一个浸没就足够了，这样的水平叫作正则值（regular value）。

定义 2.29 令为一个光滑函数. 对于一个点，若是满射的，则称是一个正则点（regular point），否则称为一个临界点（critical point）. 若，则中的所有点都是的临界点. 对于一个点，若每个点都是一个正则点，则称是一个正则值，否则称是一个临界值（critical value）. 若是一个正则值，则称水平集是一个正则水平集（regular level set）.

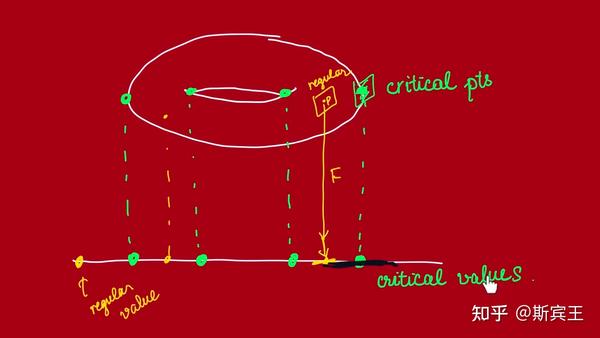
推论 2.30 一个光滑函数的每个正则水平集都是一个在中的余维度为的嵌入子流形.

证明根据引理2.6，满足为一个满射的点的集合是开的，且 . 因此，是一个浸没. 根据推论2.28，证毕.

例 2.31（球面） 球面是的一个余维度为的嵌入子流形. 根据定义，，这里是映射 . 此映射的微分是 . 这在以外的每处都是满射的. 由于，是的一个正则值，所以是一个正则水平集. 根据推论2.30，它是一个余维度为的嵌入子流形.

事实上，虽然不是每一个正则水平集都是一个嵌入子流形，但是它在局部一定是。

3 李群

现在，我们可以引入李群（Lie group）的概念了。简单来说，李群是一个群，同时也是一个光滑流形。

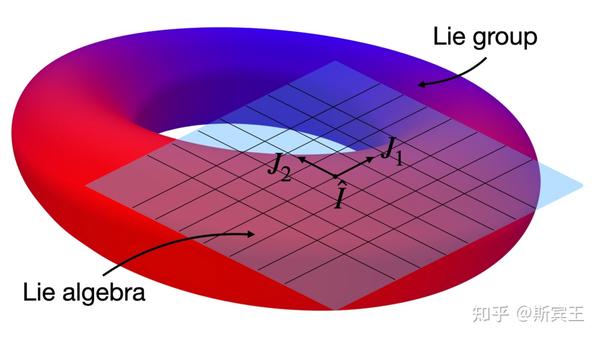定义 3.1 一个李群是一个光滑流形，它同时是一个群，且群运算是光滑映射和 . 我们将的单位元素（identity element）写作 .

李群和李代数

乘法映射界定了两个重要的的微分同胚（diffeomorphism）的族，它们是左平移（left-translation）和右平移（right-translation）映射，这里：这些都是光滑映射。令为映射，它显然是光滑的，故是光滑的。类似地，是光滑的。由于是双射，且它们的逆是光滑的，所以对于所有的都是微分同胚。事实上，乘法的光滑性本身就足够定义李群。

引理 3.2 若是一个光滑流形，它的乘法映射是光滑的，则是一个李群.

证明令为映射 . 根据假设，是光滑的. 是一个双射，它的逆是 . 我们将要证明，是一个局部微分同胚. 由于是一个双射，它是一个微分同胚，故它的逆是光滑的. 因此，映射是光滑的，故映射是光滑的.

为了证明是一个局部微分同胚，我们要计算的微分. 由于，我们有令为光滑曲线，这里，，， . 根据定义，对于任意，根据链式法则，得到根据定义，因此，我们知道是微分同胚，所以和是同构. 假设，则，且 . 那么，，又因为是一个同构， . 因此，是单射的. 由于定义域和陪域的维度相等，都是，是一个线性同构. 根据反函数定理（inverse function theorem），是一个局部微分同胚.

3.1 例子

第一个李群的例子是可逆矩阵群（group of invertible matrices）。

例 3.3（一般线性群） 令为域上的可逆矩阵的一般线性群（general linear group）. 当，它是上（维度为）或上（维度为）的矩阵的向量空间的开子集. 因此，根据例1.20，它是一个维度为或的光滑流形. 由于矩阵乘积是一个光滑映射，和都是李群.

一个李群的子群也是一个李群.

引理 3.4 令为一个李群，并令为一个子群，同时也是一个嵌入子流形（embedded submanifold）. 那么，也是一个李群.

证明根据定义，包含映射（inclusion map）是一个光滑嵌入，所以是一个光滑流形. 由于是一个子群，它的乘积映射是的乘积映射在上的限制，即 . 这是光滑映射的复合，所以是一个光滑映射.

满足上述引理的条件的子群叫作一个（嵌入）李子群（Lie subgroup）。下面我们给出很多李群的例子，它们大多都是和的李子群。

例 3.5 （1）（实数和复数的乘法群） 和是实数和复数的乘法群.

（2）（行列式为正的可逆矩阵群） 的子群由行列式（determinant）的可逆矩阵构成. 由于，且，所以它是一个子群. 由于的连续性，它是一个开子集，故它是一个余维度（codimension）为的嵌入子流形. 因此，是一个李群.

（3）（特殊线性群） 特殊线性群（special linear group）和分别是和的行列式为的子群. 我们要证明它是一个李子群. 由于它是光滑映射的水平集，我们只需证明它是一个正则水平集（regular level set），即所有点都是一个正则点（regular point），即是满射的. 对于任意和，有为了证明此公式，注意到由于的光滑性，有如果是一个可对角化（diagonalizable）矩阵，即，这里是一个对角矩阵，那么由于可对角化矩阵的集合是稠密的（dense），且是连续的，所以对于任意矩阵，都有 . 那么，求导，得出对于，，故 . 这个线性映射显然是满射的，因为对于任意复数， . 那么，是光滑映射的一个正则水平集，因而是的一个嵌入子流形. 因此，是一个维度是的李群，是一个维度是的李群.

（4）（正交群和酉群） 正交群（orthogonal group）和酉群（unitary group）分别是和的 -线性和 -线性等距（isometry）. 特别地，它们分别是光滑映射和的水平集. 将值域视作由自伴（self-adjoint）矩阵构成的集合，我们得到，和都是正则水平集. 由于矩阵乘积的光滑性，和都是李群. 由于的定义函数的陪域（codpmain）的维度是， . 另一方面，的维度是，因为所有的上对角项都是独立的复坐标，即共有个坐标，且对角线上有个独立的实坐标. 因此， .

（5）（特殊正交群和特殊酉群） 若，则，故 . 事实上，有两个连通（connected）分量，由给出，它们是开子集. 由于的同态（homomorphism）性质，满足的分量是一个子群，它叫作特殊正交群（special orthogonal group），写作 . 作为一个开子群，和的维度相等.

复数的情况是不同的. 对于，，所以 . 类似于的情况，由于到圆上的映射是满秩的，子群特殊酉群（special unitary group）是一个余维度为的嵌入子流形. 因此，是一个维度为的李群.

（6）（辛群） 通过采用一个不一样的内积（inner product），我们可以对的构造进行一般化. 由于任意上的内积都有的形式，这里是一个正定（positive definite）矩阵，我们可以定义为满足的矩阵的集合. 它也是一个李群. 事实上，它是在映射的像，这给出了一个李群同态.

若不是正定的，则我们得到的不是一个流形. 然而，我们可以选取一个半正定（positive semi-definite）反对称（antisymmetric）矩阵（）. 我们可以选取一个标准的例子，它是辛群（symplectic group）是满足的矩阵的群. 类似地，我们也可以定义 . 辛群也是李群. 可以证明，若，则 .

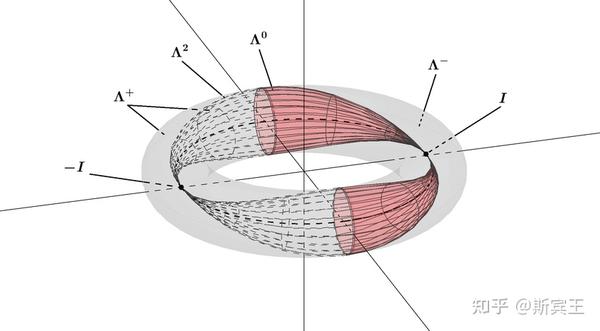Sp(1)的表示

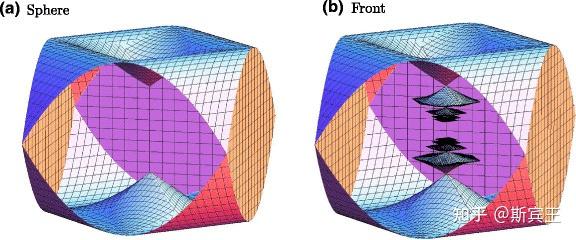（7）（海森堡群） 海森堡群（Heisenberg group）是的一个子群，它由形如的矩阵构成，这里是一个严格上三角（upper-triangular）矩阵. 它是一个流形，因为它和是同构的. 由于矩阵乘积是光滑的，它是一个李群. 有时海森堡群单指，它和量子力学（quantum mechanics）联系紧密.

海森堡群里的单位球面和单位球面的前面

（8）（欧几里得群） 欧几里得群（Euclidean group）是保持欧几里得距离（Euclidean distance）的的双射构成的群. 那么， . 由于平移映射，但它的表示矩阵（representing matrix）不在中，所以 . 事实上，中的每个元素都可以被唯一地写作，这里是一个平移映射，是一个正交映射. 我们可以将视作形如的的子群. 它是一个和同构的流形，它的维度是 .

多个李群的积也是一个李群。

引理 3.6 若为李群，则也是一个群.

例如，由于是一个李群，环面也是一个李群。

3.2 李群同态

定义 3.7 令为李群. 一个李群同态（Lie group homomorphism）是一个光滑映射，同时是一个群同态. 一个李群同构（Lie group isomorphism）是一个李群同态，同时是一个微分同胚，所以它的逆也是一个李群同构. 如果存在一个从到的李群同构，则称这两个群作为李群是同构的. 一个从到自身的李群同构叫作一个李群自同构（Lie group automorphism）.

映射是一个微分同胚，但它不是一个群同态. 因此，尽管这两个群作为流形是微分同胚的，但它们作为李群不是同构的。下面是一些李群同态的例子。

例 3.8（1）（包含映射） 若是一个嵌入李子群，则包含映射是一个李群同态.

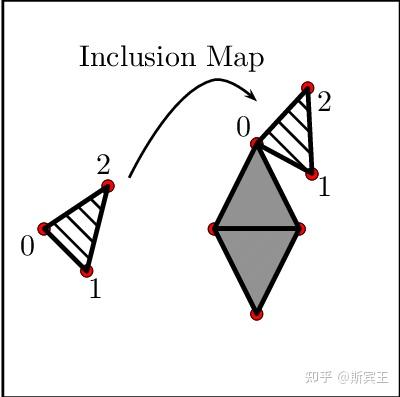包含映射

（2）（指数映射） 指数映射（exponential map）或是一个李群同态. 它是一个群之间的同态，而且是光滑的，所以是一个李群同态. 它是单射的，但不是满射的，因为它的像是 . 事实上，是一个李群同构，因为它的逆也是光滑的. 在的情况中，指数映射是满射的而不是单射的，它的核（kernel）是 .

从北极看地球的指数映射

（3）（从实数域到单位圆的映射） 映射是一个满射的李群同态. 它的核是 . 类似地，映射是一个核为的李群同态.

（4）（行列式） 行列式是一个李群同态，这里 . 若，则它不会是一个同构.

（5）（内自同构） 令为一个李群，并令 . 的内自同构（inner automorphism）是映射 . 它们是群同构，所以是李群自同构. 注意，若一个子群满足，则称是正规的（normal）.

李群同态是最好的一类光滑映射，因为它们是常秩的.

定理 3.9 每个李群同态都有常秩.

证明令为李群，并令为一个李群同态. 令，并令和分别为和的单位元素. 由于是一个同态，有即 . 等式两边同时在单位元素处取微分，根据链式法则，得到由于和是微分同胚，它们的在任意点的微分都是同构，所以和的秩相同. 由于是任取的，是常秩的.

此结论的一个推论指出，李群同态和李群同构的关系与群同态和群同构的关系是一样的：它们都只需要一个双射条件。

推论 3.10 一个李群同态是一个李群同构当且仅当它是一个双射.

证明 “仅当“的方向是同构的定义. 对于“当”的方向，根据全局秩定理（global rank theorem），由于李群同态是常秩的，若它是一个双射，则它是一个微分同胚，因而是一个李群同构.

3.3 李子群

引理3.4指出，若一个李群的子群是一个嵌入子流形，则是一个李群. 最简单的例子是一个开子群. 然而，若想要一个开子流形成为一个子群，则有很严格的限制。

引理 3.11 若为一个李群的开子群，则是一个嵌入李子群. 此外，是闭的，因而是的连通分量的一个并集.

证明任意开流形都是嵌入的，所以根据引理3.4可以得到第一个结论. 对于任意，左陪集（left coset）是开的，因为它是一个开集在一个微分同胚下的像. 任意群的陪集都是不交的，所以是除了之外所有陪集的并集. 那么，是开集的并集，因而是一个开集，所以是闭的. 因此，是闭开的（clopen），因而是连通分量的一个并集.

事实上，一个李群的所有分量都是微分同胚的。下面的结论和包含的分量有关。

命题 3.12 令为一个李群，并令为的一个邻域. 那么，

（1）由生成的的子群是开的；

（2）若是连通的，则由生成的子群是连通的；

（3）若是连通的，则生成 .

证明（1）令为单位元素的一个邻域，并令为它生成的一个子群. 令为中等于中个元素的积的元素的集合，故 . 由于是一个开集在一个微分同胚下的像，是一个开集. 那么，是开的. 对于，由于且是一个微分同胚，根据归纳法，对于任意，都是开的. 因此，是开的.

（2）假设是连通的，因而也是连通的. 由于是两个交于的连通集合的并集，是连通的. 再一次应用归纳法，得到对于任意，都是连通的. 由于所有的交于，是连通的.

（3）根据引理3.11，由于是连通的，且，所以 .

包含单位元素的的连通分量叫作单位分量，写作。上述命题的第二条说，的任意连通领域生成的单位分量。事实上，我们可以说更多。

推论 3.13 令为一个李群，并令为的单位分量. 那么，是的一个正规子群，而且是唯一的连通开子群. 的每个连通分量都和是微分同胚的.

一个生成李群的好方法是通过一个李群同态的核与像。

命题 3.14 令为李群，并令为一个李群同态. 那么，是一个嵌入李子群，它的余维度是的秩.

证明此结论通过命题2.27和定理3.9得到. 由于李群同态有常秩， -水平集是一个余维度为的子流形. 一个群同态的核是一个群，所以是一个嵌入李子群.

命题 3.15 令为李群，并令为一个单射的李群同态. 那么，像有一个唯一的光滑结构，使得是一的个（不一定是嵌入）李子群，且是一个李群同构.

证明由于有常秩，且是单射的，根据全局秩定理，它是一个单射的浸入（immersion）. 根据定理2.21，是一个局部光滑嵌入（embedding），这定义了上的拓扑和光滑结构，因为是单射的. 此光滑结构显然是唯一的光滑结构，使得是一个到其像上的微分同胚. 由于是一个浸入，是一个浸入子流形. 一个群在一个同态下的像是一个群，且从继承的群乘积是光滑的. 因此，是一个李群. 根据推论3.10，由于是一个双射的李群同态，它是一个李群同构.

下面是一些李子群的例子。

例 3.16（1）（特殊线性群、特殊正交群和特殊酉群） 由于，这里，且是一个李群同态，根据命题3.14，是一个嵌入李子群. 类似地，和也是嵌入李子群.

（2）（一般线性群） 考虑映射，它把每个复项替换为一个矩阵 . 不难验证，是一个单射的李群同态，所以我们可以将视作的一个李子群. 此外，此映射的像是一个嵌入子流形.

（3）（环面） 定义为，这里是一个无理数. 那么，是一个单射的李群同态，所以它的像是一个浸入李子群. 由于此像是稠密的，它不是一个嵌入李子群. 此像的闭包（closure）是，这是一个嵌入李子群. 一般来说，若是一个李子群，它的闭包是一个嵌入李子群.

参考文献

[1] HALL, B. C. Lie groups, Lie algebras, and representations, vol. 222 of Graduate Texts in Mathematics. Springer-Verlag, New York, 2003. An elementary introduction.

[3] LEE, J. M. Introduction to Smooth Manifolds, Second ed., vol. 218 of Graduate Texts in Mathematics. Springer, New York, 2013.