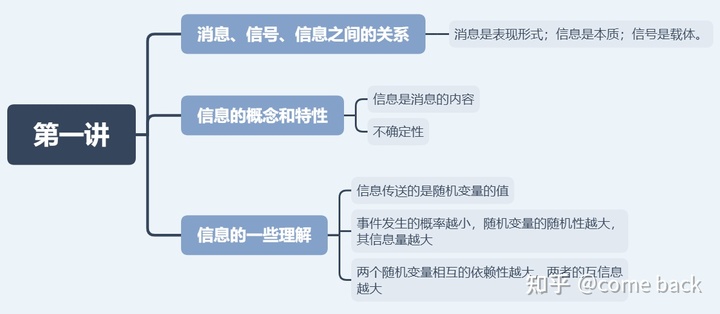
title: 《信息论与编码》课程笔记 2 自信息量的相关概念 - 知乎
category: default
tags:
- zhuanlan.zhihu.com
created_at: 2021-05-24 08:46:29
original_url: https://zhuanlan.zhihu.com/p/355627825《信息论与编码》课程笔记 2 自信息量的相关概念 - 知乎
前情提要:
一、概率论知识复习
1.条件概率:
事件B作为条件,事件A发生的条件概率为事件AB的联合概率除以事件B的概率
同理有:
2.联合概率公式:
由上边条件概率公式可以推得事件AB的联合概率:
3.全概率公式:
4.贝叶斯公式:
先将条件概率公式写出,分母用联合概率公式展开,分子用全概率公式展开。
二、离散无记忆信源与自信息
1.离散无记忆信源的数学模型:
一个离散无记忆信源包含n个可能出现的消息组成的集合
离散信源的数学模型可以表示为:
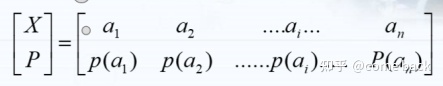
注意 :大写字母
2.自信息量的概念(描述随机事件的信息量(不确定性))
一个信源(随机事件)发出某一符号,产生某一确定的结果以后所带来的信息量称为自信息量,表示为
附:对数函数的底一般取2,底不同,自信息量的单位不同。底数为2时,自信息量的单位称为比特(bit),以e为底时,自信息量的单位称为奈特(nat)。具体如下:
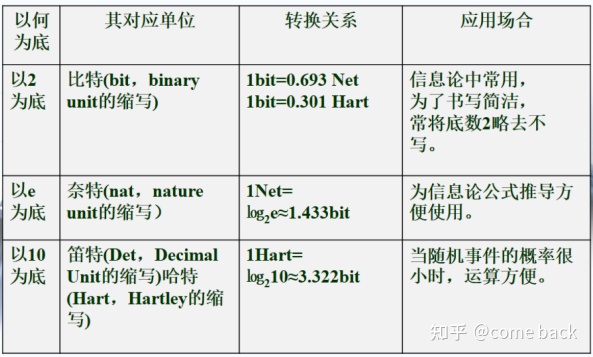
3.自信息量的意义:
随机事件
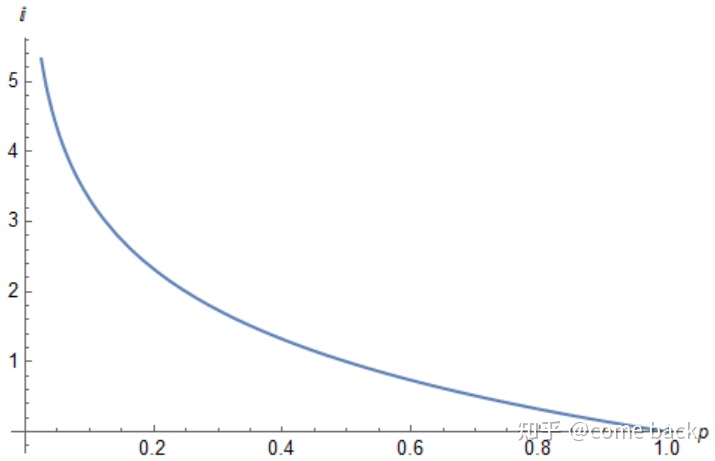
4.自信息量
- 当事件
- 当事件
- 可加性 (有条件):对于 两个相互独立的事件
、 - 非负性 :由于
- 自信息量
三、其他自信息量及其之间的关系
1.两个随机事件离散信源的数学模型:
两个随机变量
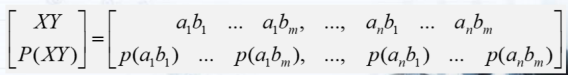
2.联合自信息量的概念:
顾名思义, 两个随机事件联合事件的自信息量就是联合自信息量 。表示为
特殊性质:如上文提到的自信息量的可加性, 当两个随机事件
3.条件自信息量的概念:
顾名思义,一个条件概率对应的自信息量即为条件自信息量。表示为
4.自信息量、联合自信息量、条件自信息量之间的关系:
由以上公式,有
即满足
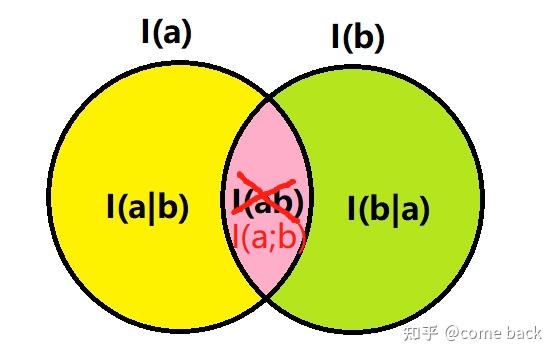
可以参照下图进行理解和记忆:(中间粉色区域为互信息,第4篇中有讲到)
欢迎在评论区交流问题~
编辑于 04-22
文章被以下专栏收录 信息论学习笔记 记录信息论知识
原网址: 访问
创建时间: 2021-05-24 08:46:29
目录: default
标签: zhuanlan.zhihu.com