物理学中的群论 · 入门篇 第〇章：概述

单看“群论”这俩字，很多初学者就被吓到了：群是个啥，有啥用，物理人为啥要学这么难的数学？然后就有了畏难情绪；或者随手翻开一本群论教材的目录，映入眼帘的是一堆陌生而奇怪的名词：群表示论？李群？李代数？这是物理人能学懂的东西吗？跟物理有什么关系？我相信很多普通的初学者都有过类似的感受.

但实际上，任何概念在第一次看到的时候都会显得陌生而困难，即使它可能很简单；所以在本系列文章中，我尽量避免一开始先引入令人困惑的名词（有些名词甚至容易让人望文生义），而是 首先从熟悉的角度或是某个亟待解决的问题引入概念 ，最后再点名概念的名字，这样更加容易让初学者接受. 若是此前偶然见过这些名词但不理解其内涵，此时你会有豁然开朗之感.

至于群论在物理学中的重要意义，这里只能针对初学者做简要的介绍. 群论是描写对称性的数学语言 ，所以凡是物理学中与对称性有关的部分，都离不开群论. 比如你可能知道对称性与守恒律的关系，实际上动量、角动量一类的基本守恒量，其准确定义就离不开群论，尤其是量子力学中对自旋的理解，如果不用群论的语言就会很迷糊； 对称性是系统在特定变换下的不变性 ，那么所有物理学分支中与对称性有关的部分都需要群论来描述，比如狭义相对论中的 协变性，场论中的规范不变性，晶体中的离散平移对称性等等. 本系列文章会具体地介绍这些物理的对称性，作为群论的重要应用.

既然群可以用来描述特定变换下的对称性，那我们不妨先来考察一下 变换 是什么东西.

举个例子：考虑一个圆，单纯几何的圆，并以圆心为原点建立一个坐标系. 再考察在这个平面内以原点为中心的转动，这里有两种理解方式：坐标系不动，圆转动；圆不动，坐标系转动. 这两种处理方式完全等价，习惯上采用坐标系不动的观点. 易知圆做任何转动变换后仍是本身，所以对于圆这个系统，转动变换是一个 对称变换 ，也说圆具有（二维）旋转 对称性.

变换的描述：规定一个转动的正方向后，任何一个转动 可由一个参数旋转角 来唯一地标记（ ），每一个这样的转动 就是一个变换，此外还可以定义转动变换的 合成 ：首先做转动 ，再做转动 ，这样的连续的两次转动等价于另一个转动 ，定义转动合成的记号“ ”，满足 ，则易知这个转动合成“运算”有下列性质：

1. 对于任意转动 ，它们的合成转动 也是一个转动；（看起来是废话）
2. 对于任意转动 ，满足 ；
3. 存在一个转动 ，其转动角为 ，对应于不做转动，称为单位元；
4. 对于任意转动 ，存在一个转动 满足 ，记作 ，称为 的逆.

实际上，不仅仅是转动变换，许多对称变换的合成都满足上述性质（比如空间平移变换、三维转动变换等等）；既然这是这些变换的公共性质，我们不妨 直接研究这些性质本身 ，看看这些基本性质能得到哪些进一步的结果，那么这些结果对于所有满足上述性质的对称变换就都适用. 于是，数学家把满足这些基本性质的东西定义为一种数学对象，称为 群 ，研究群的数学分支就是群论. 这样，群论的所有结论都可以直接应用到对称性于对称变换的研究中，为物理上的研究减轻了负担.

由上述讨论，我们可以自然地引出群的标准 定义 （实际上就是将上述性质抽象化）: 若对于一个集合 ，其中有一个运算“ ”，满足下列性质：（集合的记号 是Group的缩写，小写 表示元素，下标 表示任意，非常自然而合理）

1. 封闭性 ：对于任意 ，有 ；
2. 结合律 ：对于任意 ，有 ；
3. 单位元 ：存在 ，使得对于任意 ，有 ;
4. 逆元 ：对于任意 ，存在 ，使得 .

则称集合 为一个群，其中运算“ ”称为 群乘法 ，习惯上常常省去不写，直接将群乘法记作 .

其实群只是一个很普通的概念，有很多不能视为变换的东西也满足上述群的定义，因此也是群；来看一些简单的例子，大家可以自行验证是否符合群的定义：

1. 非零实数集 乘法群 ：群乘法就是实数的乘法；验证：任意两个非零实数的积还是实数；实数乘法满足结合律；单位元是 ；任意非零实数 的逆元是 ；
2. 实数集 加法群 ：群乘法就是实数的加法；验证：任意两个实数的和还是实数；实数加法满足结合律；单位元是 ；任意实数 的逆元是 ；
3. 集合 ：群乘法就是实数的乘法，单位元就是 ；
4. 整数集 加法群 ：群乘法就是整数的加法，单位元是 ；
5. 非奇异矩阵群 ：集合为所有非奇异矩阵，群乘法就是矩阵乘法，单位元就是单位矩阵；由于矩阵非奇异，所以都存在逆矩阵作为乘法逆元；
6. 一维平移变换群 ：集合为所有一维空间中的平移变换，群乘法是两次平移变换的合成，单位元就是不做平移；
7. 三维转动变换群 ：集合为所有三维空间中的转动变换，群乘法是两次转动变换的合成，单位元就是不做转动；
8. 魔方转动群 2：首先定义魔方的状态是所有棱块与角块的一种可能排列，魔方转动群的群元是任意一种状态到另一种状态所需的操作序列（对于一定的初末态，可能不唯一）；验证：任意做两个操作序列，魔方还是魔方（废话）；魔方转动操作满足结合律；不对魔方做操作即为单位元；将任意操作逆序复原，即得原操作的逆元；

由上述例子可知，群并不是什么神秘的东西，很多东西都是群，这也正说明了群论应用的广泛性.

群论，顾名思义就是 研究群的性质 的数学分支，具体而言就是研究上述四条公理能够推导出什么结论，如果再附加一些其它的定义/公理又能够得到什么结论. 得到这些结论之后，只要我们能判断某个集合是一个群，就能直接套用这些结论了.

既然群的定义如此简洁，满足群定义的集合非常多，我们不妨按照一些基本性质，对群分类进行研究，以减轻研究负担：

• 群首先是个集合，按照群元素的个数，首先可以分为 有限群 与无限群，无限群又可分为离散群（即“可列无穷”）与连续群；其次，就像数学分析中研究的“光滑”函数一样，“光滑”的连续群也有很重要的地位，我们把这种群称为 群（李群） （就像物理人不那么需要关心光滑函数的严格定义一样，我们也不用关心 群的严格定义，初学的时候你就把它等同于连续群就行）. 而至少对于物理学而言，两类最重要的群就是有限群与 群. 实际上，两类群的性质既有联系，也有很大的差异. 举例 说明三种群的差异：有限群——例如上文中3、8；离散群——例如上文中4； 群——例如上文中1、2、5、6、7；
• 群除了是一个集合，其中还定义了一个运算——群乘法，因此还可以根据群乘法的性质分类. 若对于任意群元 ，群乘法满足 交换律 ，则称该群为交换群或 阿贝尔群 ；否则为非阿贝尔群. 例如上述例子中，1、2、3、4、6都是阿贝尔群，5、7、8是非阿贝尔群.

既然我们要研究群的性质，那有什么性质可以研究呢？观察群的定义可以知道，群的性质主要体现在 群乘法 的性质，所以群乘法相似的群，其性质也差不多，无需重复研究，又可以减轻研究负担（“数学是偷懒的艺术”——沃兹基硕德）：

• 观察例子中的2和6，我们发现一维平移变换可以与实数一一对应，即任意一个平移变换都可以用向右平移的距离来描述，并且满足：向右平移 变换与向右平移 变换的合成等价于向右平移 变换，也就是说，平移的合成运算于实数加法的规则严格一一对应；所以在群的意义上，2、6两个群完全等价，我们称这两个群之间为 同构 关系. 更一般地，同构可以定义为： 对于群 与群 ，若存在双射（一一映射） ，使得两个群的群乘法满足 ，则称群 与群 同构. 两个同构的群在群的意义上完全等价，因此所有群方面的性质都完全一致，所以在群论里一般只研究一类互相同构的群中的一个代表；
• 观察例子中的1和3，两个群群元数量不同，不可能构造一一映射；但是可以构造 满射 ，其中正实数均映射为 ，负实数映射为 . 易知此时仍然满足 ，与同构的差别仅仅在于从双射变为满射，可以粗略地理解为“没那么同构的同构”，数学上将这种关系定义为 同态 ，记作群 同态于 群 . 易知同构关系是一种特殊的同态关系. 非同构的同态由于无需双射，所以其中的“小”群只能反映另一个“大”群的 部分性质 ，而有一部分信息无法反映. 这里用一个（随手画的）示意图来描述同构关系：其中群 仅有三个群元，群 可以分为三部分，群 中的每个部分于群 中的群元一一对应，则 两个群为同态关系. 所以群 将群 中一部分群元的信息“压缩”成了一个群元，只能反映部分性质，同一部分内群元的差异被抹去. 注意 ：同构关系是一种等价关系3，但同态不是.

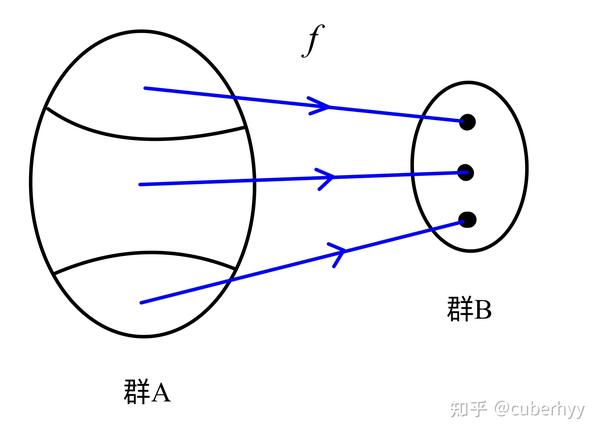
群的同态关系

• 除了同态以外，还有另一种反映群的部分性质的方法. 既然群乘法对于群的性质而言十分重要，我们不能改动它；而要反映一个集合的部分性质，我们自然地会想到要研究它的子集. 那么结合以上两点，我们可以研究一种特殊的子集，在这个子集中，原群的群乘法所满足的公理依然成立；换句话说，这个子集也是一个群，并且与大集合拥有相同的群乘法. 我们把这种特殊的子集叫做 子群. 子群的性质即可反映群的部分性质.

定义了群的同构与同态之后，群的性质的研究就大大减负了，但是我们还是觉得群乘法运算太过于抽象，既不便与直观理解，也不便与群乘法运算，如果能用一个 直观 的东西来描述群与群乘法就好了！还真有：

• 我们刚刚引入了群的同构与同态，并且知道了对于一个待研究的群，如果能找到一个既便于描述又便于做群乘法的“好”群与其同构（同态），那么我们就可以用这个“好“群来完全（部分）地描述待研究群的性质！
• 幸运的是，数学家发现有一类群可以很好的满足上述条件，那就是 非奇异矩阵群 ，这也是我要在例子中提到它的原因；矩阵群形式非常具体，就只是一些数表，矩阵群的乘法法则也就是矩阵乘法，非常方便计算4.
• 所以，我们只需要找到一个矩阵群，它与待研究群同构/同态，就可以直观地理解群元素与群乘法了！我们把这样的矩阵群叫做待研究群的 表示 ，某个群元对应的矩阵称为该群元的表示矩阵，研究表示矩阵的群论分支就是 群表示论.

群表示论几乎是群论中 最重要 的内容，尤其是对于群论的物理应用而言；例如粒子的自旋就与某个 群的表示有关，后续文章中会详细介绍. 同一个群会有很多个不同的表示，群表示论的研究重点之一就是研究这些表示的性质，例如：有多少表示？表示如何分类？不同的表示有何特点？ 群表示的性质也侧面反映出群本身的性质.

• 表示的分类：既然表示矩阵群可以与待研究群同构/同态，我们把同构的表示称为 忠实表示 ，它反映了群的所有形式；同态但不同构的表示称为非忠实表示，它只能反映群的部分性质.
• 表示的 维数 ：表示矩阵的阶数即表示的维数.

根据上述讨论，我们提炼出物理学专用群论的两组关键词： 有限群 / 群 ； 群的性质 / 群表示的性质. 所以排列组合一下，本系列文章数学部分的内容就大体分为以下四个部分：

• 有限群的基本性质；
• 有限群的表示；
• 群的基本性质；
• 群的表示.

在这些内容的基础上，会介绍对应的物理应用（放心不会很难，太难的我也不会啊）. 同时，考虑到物理上的应用，除了介绍群的公共性质以外，还会重点介绍几个在物理中有广泛应用的群及其表示.

最后，大致列一下我读过的教材与讲义，供初学者参考（ 点击书名可进入下载链接，需要 ）：

1. A. Zee, Group theory in a nutshell for physicists，经典教材，深入浅出，语言轻松幽默，非常适合作为入门的第一本书； -- file: Group theory in a nutshell
2. 李新征， 群论及其在物理学中的应用导论，北大物院群论I课程讲义，偏向口语化，可读性强，并且都是最基础的内容，难度不大；
3. Wu-ki Tung, Group Theory in Physics，经典教材，内容充实，体系清晰，但个人觉得有一点难懂；
4. 马中骐， 物理学中的群论：李代数篇 /物理学中的群论（第2版） ，很好的中文教材，但略难，部分章节可能不太适合作为入门的第一本书；这两本书在内容上有大量重复，入门读者建议选择前者，本系列标题就是化用了李代数篇的标题；
5. Nathan Carter, Visual Group Theory，比较小众的入门书籍，可以用来图一乐，有大量制作精良的图片，如果时间充裕就值得一看，缺点是基本只囊括了一部分有限群的基础知识，连群表示都没有提到（所以说是图一乐）. -- file: Visual Group Theory 最后一页有个凯莱图, 不全不止这几页

值得一提的是，前四本正经书的作者都是中国人/华人，这并非我刻意为之，而是经典教材确实就是这么几本. 除了经典教材以外，知乎上还有一些非常优秀的notes与回答，这里大致罗列一些我看过的：

1. @東雲正樹 ，東雲正樹：群论 (Group Theory) 终极速成 / 物理系零基础火箭级 notes， 老师的经典系列文章，知识点丰富，水平很高. 但也许是“火箭级“的缘故，似乎不太适合一般初学者（比如我，但是高智商大佬除外）； -- 群论 (Group Theory) - 终极速成-物理系零基础火箭级-notes
   3
2. 如何直观地理解群论？这个问题里的回答质量很高，很适合初学者阅读，以获得对群论的直观了解. 但各位大佬从各个不同的角度切入，相对来说不那么系统、完整； #check

似乎主要就看过这俩（当然里面内容很多），另外还有一些文章我没细看，就不列出来了.