title: 物理学中的群论 · 入门篇 第三章:转动变换群
permalink: https://zhuanlan.zhihu.com/p/677643396
author: Frank Hua
author_id: fb6f6991d7cf973c43e94f6319554b6d
column: 物理学中的群论 · 入门篇
column_id: c_1532040361488310273
voteup: 156 赞同
created: 2024-01-14T10:07:51
updated: 2024-01-21T15:30:49
fetched: 2024-05-17T21:09:05
count: 约 9973 字
version:
tags: [物理学, 数学, 量子物理, Frank-Hua, 物理学中的群论-·-入门篇]
url: https://zhuanlan.zhihu.com/p/677643396
物理学中的群论 · 入门篇 第三章:转动变换群
from 专栏 物理学中的群论 · 入门篇
话题:
物理学, 数学, 量子物理, Frank-Hua, 物理学中的群论-·-入门篇
正文:

物理人学群论,归根结底还是为了物理服务的,而群论在物理学中最主要的应用之一就是关于 时空对称性 的讨论:包括空间平移对称性、空间转动对称性、空间反演对称性、时间平移对称性与时间反演对称性等等。每一种对称性都对应一种时空变换,而每一种变换都可以构成一种群,其中空间反演变换和时间反演变换都可以由前几章的有限群描述,但是空间平移变换、空间转动变换以及时间平移变换都是 连续变换 ,需要新的理论。
因此从这一章开始讨论可描述连续变换的「连续」群,其中包含无穷多个连续的群元。但正如物理人学高数的时候默认「函数」就是「光滑函数」一样1,我们只关心一种「性质良好」的连续群—— Lie群 。正如物理人不关心光滑函数的定义一样,在初学阶段也没有必要纠结Lie群的具体定义2,只需要通过一些具体例子来感受就好3。甚至为了进一步简化,我们将局限于讨论 矩阵Lie群 ——也就是群元均为
〇、代数知识补充
这里讨论的矩阵都默认为
1. 矩阵的幂与矩阵指数
类似于实数的幂运算,可以定义 矩阵的幂运算 :
2. Levi-Civita记号
类似于Kronecker delta
3. Lie代数
一般语境下「代数」一词指的就是一个数学分支「代数学」,但实际上「代数」也指一种特定的代数结构。这里我们关注一种特殊的代数:
- Lie代数 。设有一个复数域
- 对于任意
- 对于任意
- 对于任意
但这个定义有点抽象,那不如举一个物理人熟悉的例子:
- 例 : 三维欧式空间
在矩阵Lie群的相关讨论中,Lie代数一般都是以矩阵为元素的矢量空间。由于矩阵自带一个矩阵乘法运算,我们可以自然地由矩阵乘法构造出一个运算
4. BCH公式
Baker–Campbell–Hausdorff公式 (简称BCH公式):对于任意同阶矩阵
其中
一、二维转动群
首先考虑最简单的一种转动群—— 二维转动群 ,其由二维平面
考虑二维平面中任意一个矢量[8]
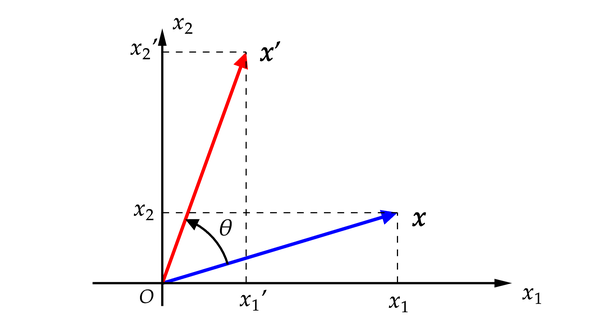
二维平面中的转动变换
由图中几何关系,不难证明
- 对于矩阵乘法运算,任意给定两个转动矩阵
- 由矩阵乘法的性质,
- 对于
- 对于任意转动矩阵
由以上四条性质不难看出, 若将矩阵乘法作为群乘法,则所有二维转动矩阵构成一个群 。利用转动变换不改变矢量长度的性质,可得
另外,通过将
即两个转动的合成等价于转动角之和的一个转动。
二、三维转动变换
现在讨论相对复杂的情形——由三维空间
1. 三维转动变换的几何
相较于二维平面中的转动,三维空间中的转动更为复杂,我们用 轴角参数化 来标记特定的转动:首先选取一个单位矢量
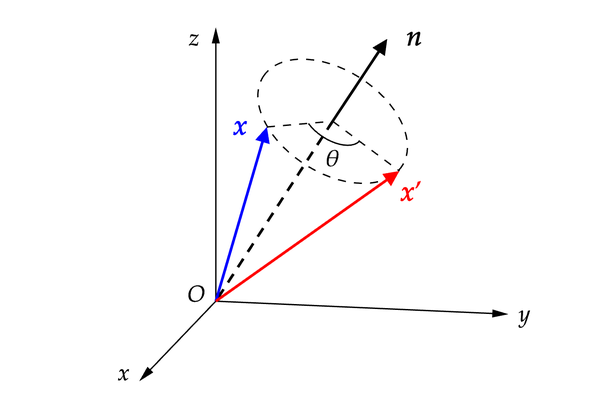
三维空间转动的轴角参数化
所以转动后矢量可以表示为
与二维转动相同,所有三维转动矩阵的集合也构成一个群,其单位元为单位矩阵
2. 三维转动群及其Lie代数
从
即
三、Lie群与Lie代数关系的推广
前两部分主要讨论了二维转动群
这里不加证明地给出,对于任意一个
最后补充一下矩阵Lie群的严格定义[14]:首先将所有
- 给定
不难验证,本文定义的
[4]: 参考:
[5]: 这一条看着很复杂,其实就是Lie括号对两个输入都是线性的,而且这个性质在量子力学中计算各种对易关系的时候可以直接用
[6]: 这一条看着很重要,但其实物理里面用不上
[7]: 本文均使用Einstein求和约定
[8]: 上标T表示转置,即将矢量视为列向量
[9]: orthogonal
[10]: special
[11]: 这是哥特体的小写英文字母,专门用于表示Lie代数,LaTeX代码为\mathfrak
[12]: 推导很简单,具体可参考:
[13]: 参考:
[14]: 没什么用,主要是说明一下这玩意存在一个可以理解的严格定义
[15]: Hall, Brian C., and Brian C. Hall. Lie groups, Lie algebras, and representations. Springer New York, 2013.
评论:
梁以: 是不是这么理解:三维旋转可以用3乘3矩阵表示,旋转的复合就是矩阵按顺序相乘。但矩阵很复杂,乘法也不好算。我们可以把矩阵变成成几个简单矩阵组合的指数形式,把乘法变成对易计算,在某些情况下计算会简单一些。直接算乘法就是李群,指数形式就是李代数。感觉有点像傅里叶变换里时域和频域的关系🤔
Frank Hua -> 梁以: 基本可以这么理解👍 不过从物理的角度,介绍Lie代数的主要目的还是引出量子力学中的角动量,这部分内容后面的文章会写[调皮] (1 赞)
梁以 -> Frank Hua: 很期待[可怜] (1 赞)
fhw -> Frank Hua: 博主,有木有PDF版本😝
Frank Hua -> fhw: 可能全部写完之后会整理一份吧 敬请期待[调皮] (1 赞)
fhw -> Frank Hua: 已经关注您了👍😝
Frank Hua: 时隔一年多,终于更了被催更最多的一篇( (3 赞)
流年: 写得很好 (1 赞)
fhw -> 流年: 全靠知乎博主友友,了解这些高端数学物理知识了
椒盐: 终于更了🧡 (1 赞)
一文: 请教一下,电磁学中有群论的应用吗
知乎用户: 感谢作者👍
Guan: 是手机版本的显示问题吗,公式不清晰😱