ScienceTechs

如何通俗易懂地讲解什么是 PCA（主成分分析）？ - 论智 的回答

问题描述

博主没学过数理统计，最近看 paper 经常遇到，但是网上的讲解太专业看不懂，谁能通俗易懂的讲解一下，主成分分析作用是什么？原理是什么？怎么做？成分或者因素怎么选？

话题:

统计学, 数理统计学, Principal-Component-Analysis, 概率论与数理统计, 论智

回答:

推荐CrossValidated的人气答主（top 0.11%）amoeba对PCA的解释，目前我见到的最通俗易懂的解释，循序渐进，由浅入深：

amoeba设想了一个大家庭聚餐的场景，大家突然对PCA是怎么回事很感兴趣，于是你逐一向家庭成员解释，首先是曾祖母，接着是祖母，接着是母亲，然后是配偶，最后是女儿，每个人都比上一个人内行一点。

曾祖母：我听说你正研究P……C……A。我想知道它是什么……

你： 呃，这只是一种总结某些数据的方法。看，桌子那边有一些红酒瓶。我们可以通过色泽、酒精度、年份等描述每瓶红酒。这样可以根据酒窖中每瓶红酒的不同特性编制一张完整的列表。但是其中很多属性是相关的，因此会出现一些冗余。因此我们可以通过更少的特性总结每瓶酒！这正是PCA做的。

红酒色泽。图片来源：winefolly.com

祖母：很有趣！所以这PCA检查哪些特性是冗余的，然后丢弃它们？

你： 问得好，奶奶！不，PCA并没有选择一些特性然后丢弃其余。相反，它创建一些 新 特性，结果这些新特性能够很好地总结我们的红酒列表。当然，这些新特性是由旧特性构建的；例如，一个新特性可能通过计算年份减去酸度或其它类似的组合得出（我们称之为 线性组合 ）。

事实上，PCA寻找最佳的可能特性，那些可能总结红酒列表的特性中最好的那些（在所有可能的线性组合中）。因此它才这么有用。

母亲：嗯，听起来不错，但我不确定我理解它了。你说的“总结”红酒列表的新PCA特性具体指什么？

你： 对于这个问题，我猜我可以给出两个不同的答案。第一个答案是你寻找一些在所有红酒中很不相同的属性（特性）。事实上，想象你得到了一个对于大多数红酒而言都一样的特性。那不会很有用的，对不对？红酒和红酒很不一样，而你的新属性让它们看起来都差不多了！这肯定是一个错误的总结。相反，PCA寻找能尽可能体现红酒差异的属性。

第二个答案是你寻找一些属性，这些属性允许你预测，或者说“重建”原本的红酒特性。同样，想象你得出了一个和原本的特性没什么关系的属性；如果你仅仅使用这一新属性，你不可能重建原本的特性！这又将是一个不好的总结。所以PCA寻找能够尽可能好地重建原本特性的属性。

令人惊讶的是，结果这两个目标是等效的，所以PCA可以一箭双雕。

配偶：但是，亲爱的，这两个PCA的“目标”听起来可不一样，为什么它们会是等效的？

你： 嗯。也许我应该画一点东西（你拿了一张纸巾，然后开始涂鸦）。让我们挑选两个红酒特性，也许是颜色浓淡和酒精含量——我不知道它们是否相关，但是让我们想象它们是相关的。不同红酒的散点图可能是这样的：

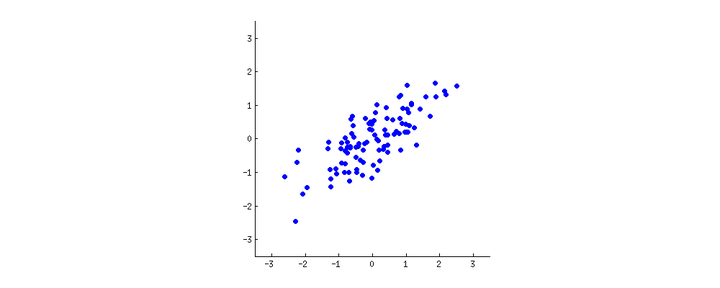
这一片“红酒云”中的每个点代表一种特定的红酒。你可以看到，两种属性（x轴和y轴）是相关的。在这片红酒云的中央画一条直线，将所有点投影到这条直线上，我们可以构建一个新属性。这一新属性将由w1x+w2y的线性组合定义，每条线对应w1和w2的特定值。

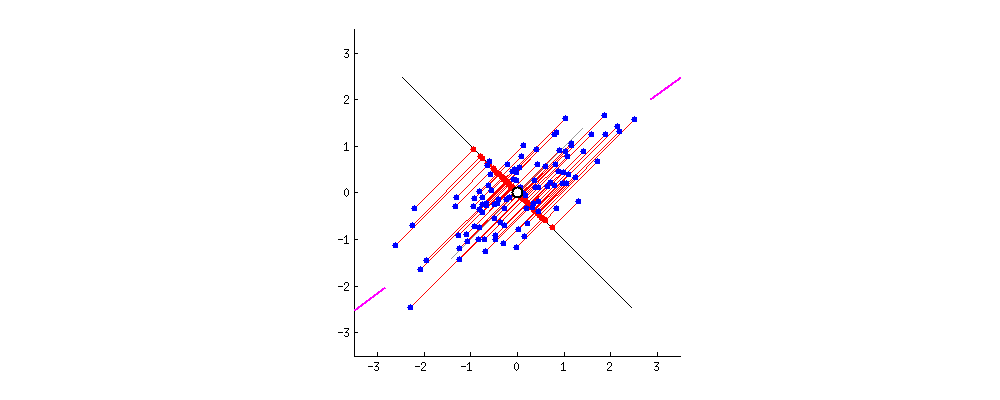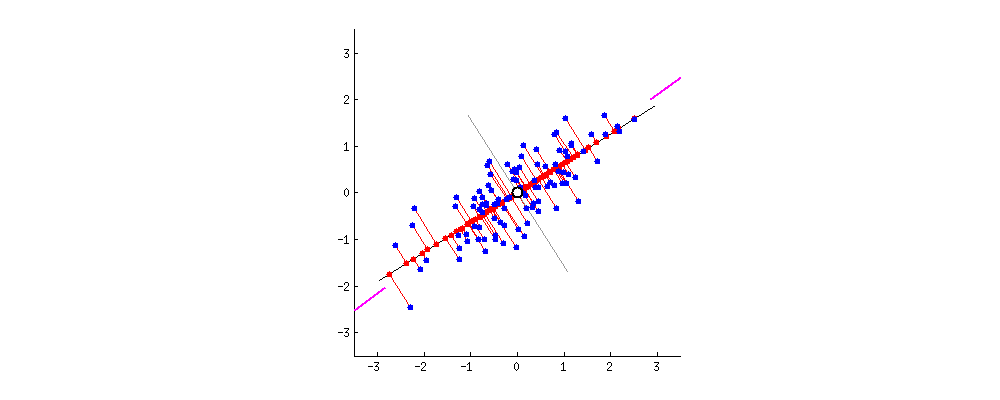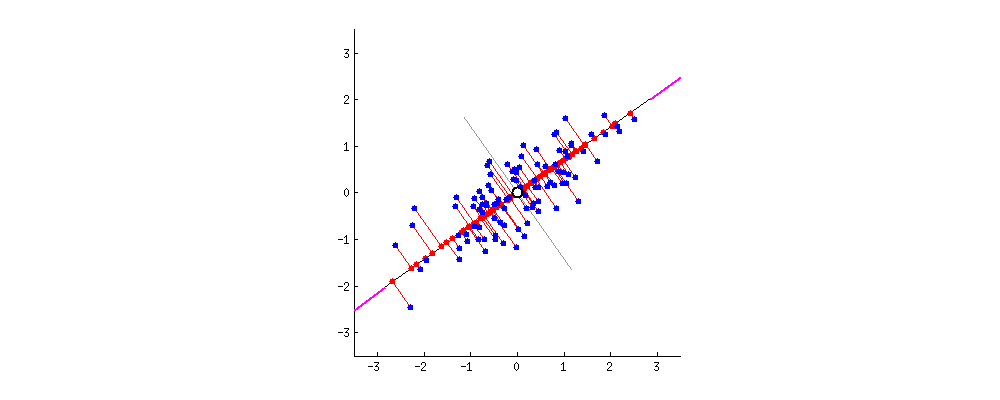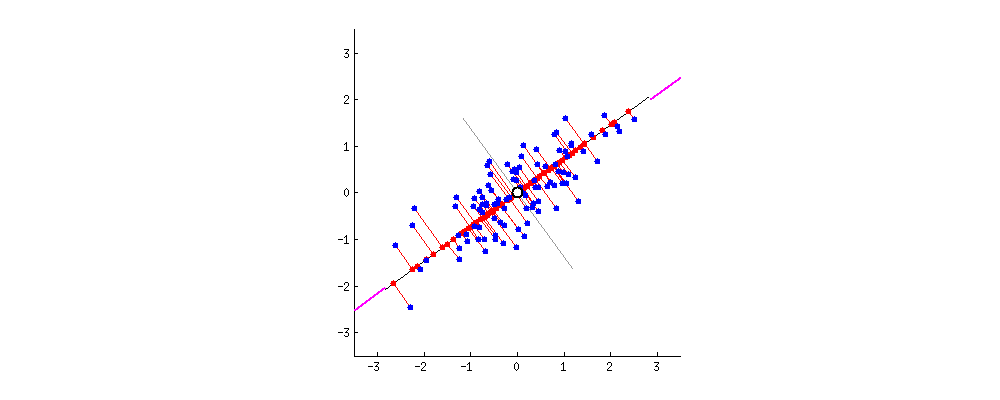
现在，看好了——下面是不同的直线上的投影会是怎么样的（红点是蓝点的投影）：

正如我之前所说的，PCA会根据两种不同的“最佳”的标准找到“最佳”的直线。首先，这条线上的差异应该最大化。注意观察当直线旋转的时候，红点是如何“散布”（我们称之为“方差”）的；你能看到它们何时最大化了吗？其次，如果我们基于新特性（红点的位置）重建原本的两个特性（蓝点的位置），连接红线的长度将给出重建误差。注意观察当直线旋转的时候，红线的长度是如何改变的；你能看到它们的总长度何时最小化了吗？

如果你凝视上面的动画有一会儿的话，你会注意到“最大方差”和“最小误差”将同时达到，也就是当直线指向我在红酒云两侧标出的品红色短线时。这一直线对应于PCA将构建的新红酒属性。

顺便说下，PCA代表“主成分分析”（principal component analysis），而这个新属性称为“第一主成分”。同时，我们通常不说“属性”（property）或“特性”（characteristic），而说“特征”（feature）或“变量”（variable）。

女儿：挺不错的，爸爸！我想我知道为什么这两个目标产生一样的结果：本质上这是因为勾股定理，不是吗？不管怎么说，我听说PCA多少和本征向量、本征值有点关系；图中它们在哪里呢？

你： 有才！从数学上说，我们通过每个红点到红酒云中心的均方根距离来衡量红点的散布；正如你所知的，这叫做 方差 。另一方面，整体的重建误差通过相应的红线的均方根距离来衡量。然而由于红线和黑线间的角度永远是90度，两个量之和等于红酒云中心与每个蓝点的均方根距离；这正是勾股定理。当然，这些均方跟距离不依赖于黑线的朝向，因此方差越高，误差就越低（因为两者之和是常数）。这里有一个以上含糊论证的准确版本。

顺便，你可以把黑线想象成硬质杆，然后把红线想象成弹簧。弹簧的势能和它的长度平方成正比（物理学上这称为胡克定律），所以杆将调整自己的朝向以最小化这些平方距离的总和。我做了一个关于它大概是什么样的模拟，加上了一点摩擦力。

关于本征向量和本征值。你知道协方差矩阵吧；在我的例子中它是一个2x2的矩阵

这意味着x变量的方差是1.07，而y变量的方差是0.64，它们之间的协方差是0.63。由于这是一个对称正方矩阵，给定它的本征向量，选用一个新的直角坐标系可以使其对角化（凑巧的是，这称为 谱定理 ）。对角上的值就是对应的本征值。在这个新坐标系中，协方差矩阵是对角化的，看起来大概是这样：

这意味着，现在点之间的相关性为零。很明显，投影的方差将由特征值的加权平均决定（我这里只描写了直觉）。因此，选择第一组坐标轴上的投影将达到最大可能方差（1.52）。由此得出，第一主成分的方向由协方差矩阵的第一个本征向量指定。（更多细节）

你也可以在旋转的图像上观察到这一点，图像上有一条与黑色直线正交的灰色直线；它们一起组成了一个旋转坐标系。试着留意在这一旋转坐标系中，何时蓝点变得不相关。答案仍然是黑色直线指向品红色的短线的时候。现在我可以告诉你我如何找到这两根短线的：它们标记了协方差矩阵的第一个本征向量的方向，在这个例子中是(0.81, 0.58)。

最后，附上生成上文中动画的

本文由原作者amoeba以cc by-sa 3.0 with attribution required许可授权论智编译，如需转载，请按许可条款规范转载。

　　

评论:

自由: 哦，看在上帝的份上，我想我应该给你个赞 (54 赞)

Toby三三 -> 自由: 哈哈哈哈哈哈这个腔接的好

mooo -> 自由: 哈哈哈哈啊哈哈哈哈哈哈哈哈哈哈啊哈哈

沪郢Iris -> 自由: 老译制腔了

西贝先森: 弹簧这个理论是真的强 (30 赞)

Jovin: 这是我目前看到的最通俗易懂的PCA解析了，感谢！ (12 赞)

阳光陈靖文:

女儿：爸爸画在纸巾上的线动起来了！我爸爸是神仙！

😳 (4 赞)

大满: 文中动画的matlab代码无法下载了。请问可以从哪里再次下载到？ (3 赞)

拾穗乃智: 牛逼 (3 赞)

知乎用户: 🐂 (2 赞)

燕小麦: cool (2 赞)

小轩子: 太强了大佬，动画怎么做的哇 (1 赞)

知乎用户: 666 (1 赞)

Interactive Graph
Table Of Contents
如何通俗易懂地讲解什么是 PCA（主成分分析）？ - 论智 的回答
问题描述
话题:
回答:
评论: