听说一切物体在时空中的速度都是光速c？| 狭相支线

相对论, 狭义相对论, 光速

相信很多人都听过这样一句逼格很高的话： 在相对论里，一切物体在时空中的速度都是光速c 。

有些人还会把“ 在时空中 ”这个定语给省略掉，就留下一句“ 一切物体都以光速运行 ”，把读者的三观震碎。然后不加一句解释就飘然离去，留下读者在那里一脸懵逼。

这个事情呢，说简单也简单，说麻烦也麻烦。但是，鉴于它超高的B格，长尾君决定好好跟大家说道说道，让你们以后可以在心仪的女生面前，在朋友的聚会里“高谈阔论”，享受知识带来的乐趣~

当然，这个问题对我们深入理解 狭义相对论 ，从牛顿力学的时空观转向相对论的时空观也大有好处。

你们觉得这个问题反常，是因为我们平常理解的 速度 都是建立在“ 空间 ”的概念上的。

什么是速度？速度就是位移除以时间。在单位时间内，我在 3维空间 里移动了多少，速度就是多少，这是我们的常规理解。

在这种理解下，每个物体的速度当然是可变的，可大可小，可快可慢。而且，我们还知道，在相对论里，任何有质量的物体，它的速度都不会超过光速。

所以，在这种语境下，我们就会觉得“一切物体的速度都是光速”非常反常，甚至非常扯淡了。即便他说了是在相对论里，你也搞不懂为什么相对论里会这样说。

要理解这句话，关键就在那个定语“ 在时空 ”里。当我们在说 “一切物体的速度都是光速c” 时，我们说的这个速度是指在 时空中 的速度，而不是我们一贯理解的在 空间中 的速度。

“ 空间 ”和“ 时空 ”，一字之差，意思却天差地别。这一字之差，也是 牛顿力学 和 相对论力学 之间的关键差别。

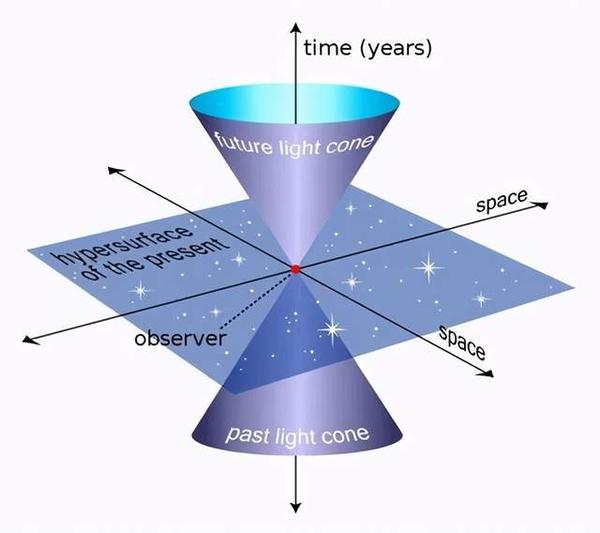
我记得我在各种场合（公众号的文章里，微信群里等）说这个说了好多次： 狭义相对论的背景是4维闵氏时空，它最基本的东西是事件。一个事件包含3个空间坐标和1个时间坐标，时间和空间在相对论这里地位平等了 。

我们之前理解的速度，都是定义在 3维空间 里的速度。一个物体从3维空间中的一个点（具有 3个空间坐标 ）移动到另一个点，我们用这个位移除以时间得到的速度。

那么，到了相对论，最基本的东西是 4维时空 ，而不再是 3维空间 。如果我们想要仿照上面的方法，在 4维时空 里定义速度，我们要怎么定义呢？

类似的，我们当然也希望， 从4维时空的一个点移动到另一个点的“时空位移”除以某种时间，得到4维时空中的速度 ，对不对？

因此，要搞定4维时空里的速度，我们就需要先搞定4维时空中的“ 位移 ”和“ 时间 ”，我们来分别看一看。

4维时空中的位移（以后就简称 4维位移 吧）好办，我在《闵氏几何是什么？它是如何统一时空并极大简化狭义相对论的？》不是教大家画过 时空图 么？就是仿照3维空间里的坐标系，我们在3维空间坐标系里再加一个时间轴，组成了一个4维的坐标系，这样画的图就是 时空图 。

这样，4维坐标系里的每一个点就有4个坐标，例如 事件点p1（x1,y1,z1,t1) 时空图里的每一个点就代表一个事件。同样，如果还有一个 事件点p2(x2,y2,z2,t2) ，那么，我们把 事件点p1 从时空图里移动到 事件点p2 的位置移动定义为 4维位移 ，这就非常合理了吧。

也就是说， 3维空间 里的 位移 ，就是我们从3维空间的一个点移动到另一个点（比如从家移动到学校）。那么， 4维时空 里的 位移 ，就是我们 从4维时空的一个事件点移动到另一个事件点 。

因为事件是有4个坐标的（3个空间坐标，1个时间坐标），因此，如果我一直坐在家里没动。那么，从3维空间来看，我的坐标点没有变化（因为x,y,z都没变），但是，从4维时空来看，我 7点在家 这个事件点跟我 8点在家 这个事件点就是两个不同的时空点了。

7点在家 的时候，你的 时空点 可能是（0,0,0,7）， 8点在家 的时候就是（0,0,0,8）了。 你的空间坐标没变，但是时间坐标变了，因此在4维时空图里，这依然是两个不同的点，因此它们之间依然有位移 。懂了么？

也就是说，即便我一直呆在家里没动，从 3维空间 的角度来看，我确实没动（因为空间坐标没变），因此 速度为0 。但是，从 4维时空 的角度来看，即便我一直坐在家里，我依然在运动（因为虽然空间坐标没变，但是时间坐标在变），因此 速度不为0 。

这个4维时空下的速度，就是我们标题里说的 4维速度 ，就是那个“ 一切物体都以光速运动 ”的速度。

相信看到这里，你应该有点感觉了。

如果你能理解我即便呆在家里没动，我依然有4维速度，那问题就解决了一半。因为剩下来的工作，无非就是 证明这个速度就是光速c，而且对所有物体都成立 。

到了这里，我请大家闭上眼睛，想象自己在 4维时空 里遨游。想象你自己的每一个瞬间，每一个动作，都在 4维时空 里穿梭，你不仅在 空间 中穿梭，也在 时间 中穿梭，在时空里飞舞。

因为时间长河永远向前奔涌，时间永远在向前流动。因此，即便你一动也不动，呆在那里傻坐着，你也被时间长河裹挟着飞速移动。

逝者如斯夫，不舍昼夜。

如果你不想在时间长河里傻坐着，你也想运动运动，学习刘翔、博尔特飞奔一波，开飞船去宇宙深处活动一下。于是，你的空间坐标就发生了改变，你就有了 空间上的速度 。

那么，空间上的这个速度会给你带来什么改变呢？

有一个但凡接触过相对论都知道的结论： 钟慢效应 。

也就是说，当你在空间上有了速度的时候，你的时间开始变慢，而且速度越快，时间减慢得越快。说得更通俗一点就是， 当你在空间上有速度的时候，你在时间上的速度就会相应减慢，你在空间上的速度越快，你在时间里的速度就越慢 。

就好像你骑着一匹赤兔马在 时空 里飞奔，由于赤兔马的最大耐力和速度是有限的。因此，当你向空间方向飞奔时，你在时间方向上的速度就慢了下来；当你朝时间方向上飞奔的时候，你在空间上的速度自然就慢了下来。

当你在 空间 里的速度达到 最小 ，也就是 静止不动 时，赤兔马所有的体力都在时间方向上冲刺，这时候时间流逝得是 最快的 。当你空空间里的速度接近最大（光速c)，你在时间里的流逝几近停滞，这就是钟慢效应的极致。

而赤兔马在时空中的速度，就是光速c，你可以按比例把它分配到时间和空间中，但是它们的“总和”保持不变 。简单来说，这就是 狭义相对论 。

如果你以后习惯了在 4维时空中 思考问题，而不再一直死守 3维空间 ，那你会觉得狭义相对论的一切东西都非常的简单自然。

相反，如果你一直试图死守在 3维 空间理解 4维 的相对论，那么，这就好像你试图通过盯着 2维 墙壁上的影子，来理解外面的 3维 世界一样。不是不可以，但是会非常非常的困难，属于纯粹给自己找不痛快。

因此，我们接下来要开始尝试在4维时空里重新理解相对论，理解相对论力学。

我们要在4维时空里重新定义 4维位移 （两个时空点之间的位置变化），重新定义4维速度、4维加速度、4维力、4维动量……

站在这样的角度，我们才能用最自然的角度来欣赏相对论力学。在这样的角度里，我们标题说的“所有物体在时空里的速度（也就是4维速度）都是光速c”就会变得理所当然。

因为你只要把4维速度的形式写出来了，你就会发现任何 4维速度的模的平方 都是 c² ，所以就有标题的结论就不足为奇了。

最后，我再补充说明一点。

我在上面定义 4维速度 时，跟大家说了 4维位移 （4维时空图里两个事件点的位置移动），这个好理解。但是我一直没有说对应的 时间 是怎么定义的。

毕竟，速度速度嘛，位移除以时间才叫速度。

我们在牛顿力学，在3维空间里定义速度都比较简单，因为牛顿力学里有绝对时间，我们直接用3维空间点的位置移动（3维位移）除以绝对时间（就是我们过去理解的时间）就可以得到速度。

但是，相对论里时间是相对的，并没有绝对时间了。那么，我们在4维时空里，要用4维位移去除以哪个时间呢？因为时间是相对的，那么，除以哪个参考系的时间似乎都不太合适。

比如，我7点从家里出发，8点到学校，你要用这两个事件点组成的4维位移除以哪个时间呢？家里的时间？学校的时间？路上的时间？

显然都不合适！

但是，有一个时间是比较特殊的，对我而言是唯一的，那就是： 我自己随身携带的时钟指示的时间 。

我从家里出门时往兜里放一块表，这块表一直跟我保持 相对静止 ，它指示的时间自然与众不同。这种 跟物体一直保持相对静止 的时钟指示的时间，叫 固有时 。

这个话题我就不在这里展开了，感兴趣的可以去看看我的9篇主线文章的闵氏几何篇，后面也会详细再说的。

最后，一句话回答 为什么说一切物体在时空中的速度都是光速c ？

答： 因为一切物体的4维速度的模的平方刚好等于光速c的平方 。

相关文章：《闵氏几何是什么？它如何统一时空并极大简化了狭义相对论？ 》

黄斌:

所以钟慢效应的原因是，物体总速度为恒量c的情况下，因为在空间中有了分量，所以导致时间上的分量减小?
这个视角挺有意思。就是不知道在现有理论上是否成立。工科生只能表示不明觉厉[流泪] (9 赞)

伏地魔 -> 黄斌: 涉及狭义相对论的课里都有讲吧 (2 赞)

黄斌 -> 黄斌: 工程人只学了大学物理(1?)[捂脸]而且也就一个洛伦兹变换、以及张量的初步概念，不记得还从这种矢量的角度来阐述光速和时空的关系。

黄斌 -> 黄斌: 对了，张量是广相里的。

放弃了思考 -> 黄斌: 这个可以证明的，数学技巧并不高

黄斌 -> 放弃了思考: 数学方面无非是矢量在时间维度的分量罢了。关键是这个理论在物理层面是否站得住，这个才是比较有意思的地方。

不死宅男: 懂了，难怪死肥宅死得快 (4 赞)

知乎用户: 解释得好清楚，其实把公式当最下面应该更好 (3 赞)

Mark: 冥想是否可以实现时光慢放？

葬爱教皇 -> Mark: 不可以。当你坐着不动冥想的时候在时间分量上跑得是最快的。

Mark -> 葬爱教皇: 可是为什么感觉很久了，看时间只过去一分钟而已？

啦啦啦 -> Mark: [惊喜]可能是你想拉稀 (1 赞)

Jinbiao Yang: 有点奇怪，如果空间速度是光速，时间速度就是1？这个时间的量纲是什么？

Jinbiao Yang -> 黄斌: 那1自然单位的时间的意义是什么？ (1 赞)

黄斌 -> Jinbiao Yang: 搞了半天理解错了你的意思，亏得还认认真真的解释了半天[捂脸]见笑见笑

啊啊 -> Jinbiao Yang: 自然单位制，光速是1。

wei jiang:

这个没意义，因为你对模的定义，希尔伯特空间，柯西公式，计算的前提都是光速是C 恒定不变， 这就像假定光速为C， 设时间T=S/C ， 然后在证明
C=S/T一样，自证逻辑自洽而已 (2 赞)

高原猎鹰: 最好把“四维”先解释清楚，否则其他的各种解释都是没有意义的。 (2 赞)

知乎用户: 这就是“概念偷换”带来的懵逼效应。四维速度恒为c，如果理解为三维空间速度的话那就真会懵。如果从闵可夫斯基时空图上来看这个问题就很好理解，速度不同的物体，它自身的参考系的空间轴和时间轴夹角在静止参考系中就不是九十度，而是一个锐角。四速度的一部分给时间轴分去了（时间轴上的投影值），另一部分就是在空间轴的投影值。两个投影值就是四速度在空间和时间轴上的分量，共同组成四速度。 (1 赞)

知乎用户 -> 知乎用户: 伽利略变换下的情况是，无论物体速度如何，空间轴会倾斜，但时间轴永不倾斜。伽利略变换中也有四速度，但这个四速度并不是恒定的量，原因就是时间轴不协调倾斜，四速度的时间分量永远是同一个值。

失得勿恤: 对的，就是 ，即四维速度的大小恒为c (1 赞)

龚宇晨:

如果计算四维速度，除的是固有时，那么默认了参考系是动系。
除的应该是观察者参考系的固有时

from: https://api.zhihu.com/articles/304192254