自学抽代的小女孩请各位大神多多赐教，不胜感激。
定义我是知道的，但是感觉理解不透。所以想向大家请教~
另外，陪集可以理解成等价类吗，它对于群的划分是怎样的呢？商集如果我没记错是所有等价类的集合，那么商群的作用是什么，为什么要通过正规子集来刻画呢？
谢谢大家~不胜感激

数学, 抽象代数, 现代数学, 群论

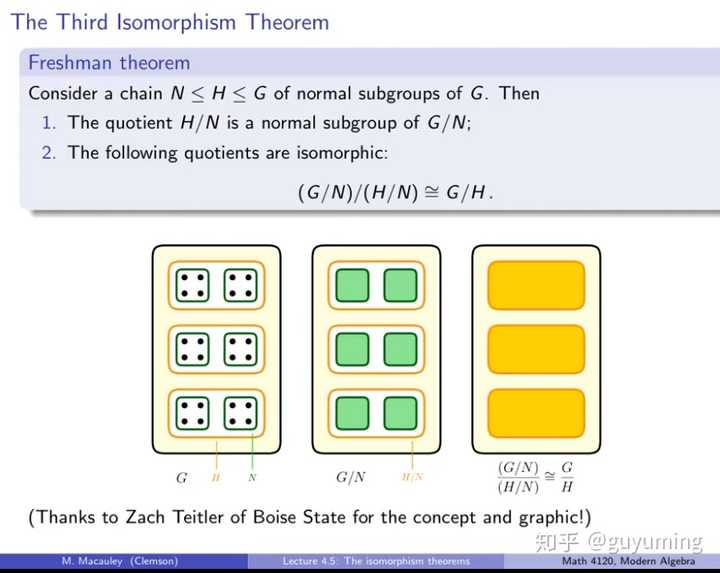
这个图其实和本问题高赞回答里面那个“一所高中分班级”的比喻有些接近的。

我个人目前对群论的体会是：图里的那些个最小单位的黑点点，不要理解为不可分的“实体”，而是“实体间的映射”或“置换”。所以这图表达的也就是子群，商群关系，却并不能体现群成员之间关系。

关于陪集和正规子群，我再从 Visual Group Theory 里截两个图：

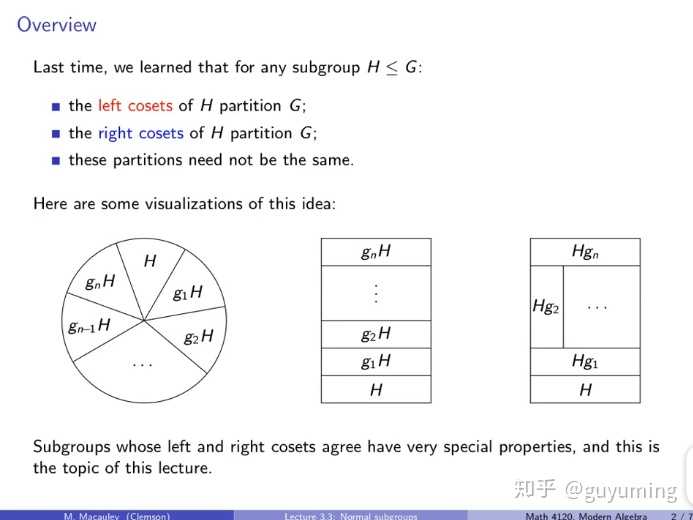
最后，索性多截两张图，来解释下前面提到的“群成员是映射”的理解：群成员是下图三角形顶点通过旋转或翻转产生的置换，也就是说群成员是初始三个顶点位置到变化后三个顶点位置的映射。

若给群成员从1到n编上号，又可以得到对称群Sn的一个子群：

关于置换，我是看懂这篇文章后才觉得自己明白的：近世代数理论基础10：变换群·置换群 。倒不是说别的文章不行，如同一顿饭吃饱了不能只归功于最后一口。 -- 近世代数 - 文集 - 简书 总计43章

再回到“群成员是映射”，我目前学到的例子里啥对称旋转翻转啊，这种映射都是空间点一一映射，也就是至少都可以理解成“函数”。结合Cayley diagram 可视化，是不是可以理解为群描述的就是定义域，值域相同的一组一一映射（也就是Generator）复合的结果及关系呢？

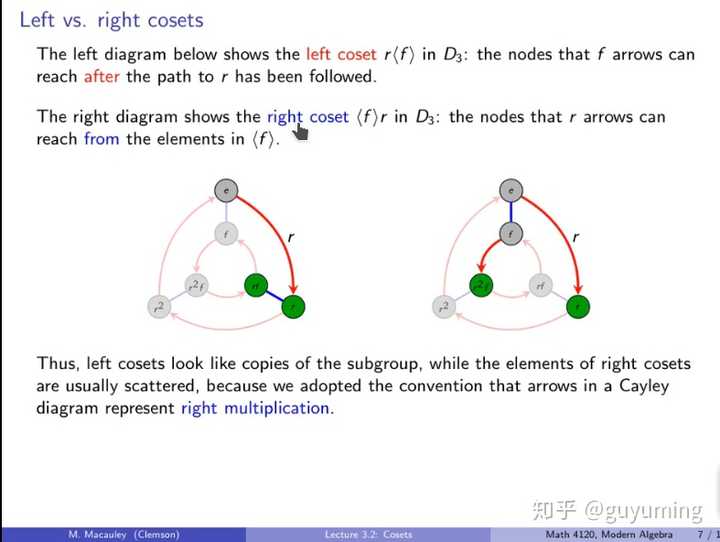
再贴两个 Visual Group Theory 里面关于左右陪集里面的比较吧。我找到两次比较，第一次出现在Cosets定义那一节，第二次出现在讲Quotients时的回顾。事实上，我一开始听 Visual Group Theory，一直觉得右陪集比左陪集容易理解，虽然从结果上说，左陪集就像子集的拷贝，容易看出，但如何根据Cayley Diagram 里面的点和箭头得到左陪集，我一直觉得脑子有些不够用。后来，看到第二次对左右陪集的对比，觉得第二次对左陪集的描述容易理解些：

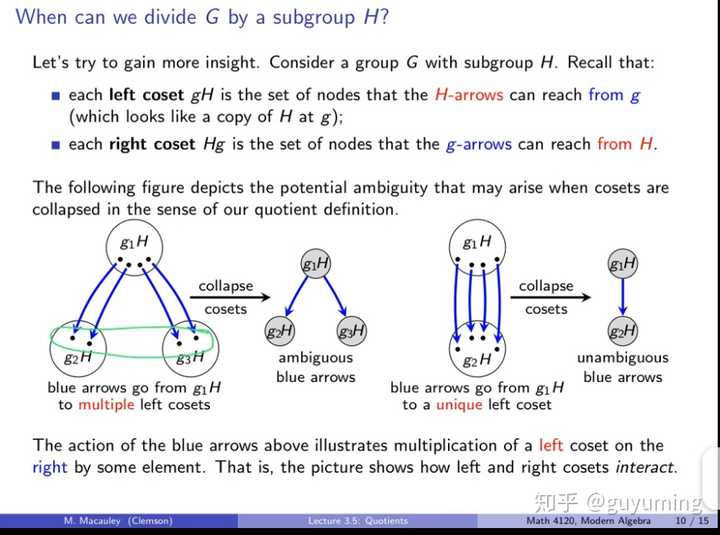
推荐阅读 为何从一元五次方程开始就没有由有限次加、减、乘、除、开方运算构成的求根公式了？ 里 “如何把门把手分层——如何把域扩张（在不破坏伽罗瓦对应的情况下）分为若干步。”那一部分，就是那个班级同学换礼物的比喻。

我一开始看匡世珉这个回答是云里雾里，后来看了好久VisualGroupTheory，搞清了一些基本定义后再看，觉得有些明白了（不排除自以为明白了，其实只是混了脸熟）。

看 visual group theory 的时候，一直不明白为啥要研究 轨道，稳定子 啥的，刚看了 如何使用GAP复原魔方？ 才有恍然大悟的感觉。

沐夏小天: 同样的困惑，为何研究轨道和稳定子呢？

from: https://api.zhihu.com/appview/api/v4/answers/1493354027