如何直观地理解群论?
问题描述
大部分同学在学习代数学时,都会被一大堆的概念搞得晕头转向。
几年前,我刚开始看线性代数时也是这样,完全不明白为什么要定义这些奇怪的东西。直到后来看到《如何直观理解矩阵和线性代数?》、《理解矩阵(一)》等文章,才豁然开朗。我非常认同《理解矩阵(一)》文中强调数学直观性的观点。
那么,应该如何直观地理解群论?群论中一些主要的概念究竟是为什么、怎么样引入的?
【参考问答】
话题:
数学, 抽象代数, 离散数学, 群论, 多项式方程, PeiLingX
回答:
最近正好学习群论有些微小的心得,对一些基础的定义和抽象概念有了一些直观理解:
群的定义、子群、陪集、正规子群、商群、直积群、同构、同态等……
虽然这些理解只涉及了群论的很小一部分,也没办法回答这些概念如何被引入,但我相信,通过构造一些几何意义比较明显的例子来说明,对于理解它们还是有些帮助的。
注:本回答内容都是一些粗浅而不严谨的个人体会和类比,各位大神若路过还请多多指正。
0) 构造三个例子
我们在这里给出三个群来作为例子,后面将通过它们之间的一些关系来理解前面提到的那些抽象概念。
群
于是群元记为:
代表着将复平面上的向量旋转
群乘法自然就是复数乘法:
群
群元直接记为实数
(
代表着将复平面上的向量变为原来的
群乘法为普通乘法:
(
群
群元可以表示成除原点外的任意复数:
(
代表着将复平面上的向量伸缩
群乘法为复数乘法:
(
( 可以证明它们各自构成一个群 )
下面就用这三个例子以及它们之间的关系,来分别理解本文开头提到的一些定义和概念。
1) 群定义的几何直观
群定义即著名的“封结妖逆”四字诀,我们来对它们一一进行直观理解。
- 封闭性 :两个群元相乘后仍然是群元
直观理解:
我们可以认为一个群代表了“某一类”变换,这些变换的叠加( 群乘法 )也属于“同一类”。
比如例子中的群中,某个群元 代表将复平面上的向量旋转 角度,群元 代表将复平面上的向量旋转 角度,而它们的乘法 也是复平面上的旋转变换( 旋转 角度 ),因此
- 结合律 :
直观理解:
结合律可以理解为连续操作的唯一性,还是以群为例:
将向量先旋转角度再旋转 角度,等同于将向量先旋转 角度再旋转 角度,结果都是将向量旋转了 角度,即:
这个条件看起来理所当然,但为了感受它对于群定义有多么必要,我们可以构造一个反例:剪刀石头布
( 这个反例来自于知乎的另一个回答,但是我忘了收藏找不到了,如果原作者看到了请前来认领…… )
如果以 {剪刀, 石头, 布} 构成一个集合,并且按照胜负规则定义所谓的乘法:
剪刀·石头=石头·剪刀=石头;
石头·布=布·石头=布;
布·剪刀=剪刀·布=剪刀
那么我们可以验证这个“乘法”不满足结合律,比如:
石头·(布·剪刀)=石头·剪刀=石头,而:(石头·布)·剪刀=布·剪刀=剪刀
这样的乘法本身就是“畸形”的,因为它无法定义唯一的“连续操作”。
- 幺元存在性 :
直观理解:
幺元很好理解,就是“什么都不做”的变换。还是以群为例:
先什么都不做( 将向量旋转零度 ),然后再将一个向量旋转角,最终结果也就是将向量旋转了 角,即: ,其中 ,就是群 中的幺元。
幺元存在性就意味着允许群元“什么都不做”,否则构不成群。
- 逆元存在性 :
直观理解:
逆元也很好理解,就是“做了又反悔”的变换。还是以群为例:
先将一个向量旋转角,再将它旋转 角,最终结果向量还在原地,等于什么也没做,即: ,其中群元 就是 的逆元。
逆元存在性意味着允许群元“悔棋”,否则构不成群,只能构成半群,因为每个群元都找不到自己的另一半。
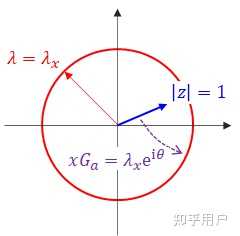
2) 陪集的几何直观
先来看群
显然,
另一方面,如果我们取伸缩系数
而由于
直观理解:
它的几何意义,是将复平面上的单位向量变换到半径为的圆上的任一点的所有变换的集合,我们不妨就将它视为半径为 的圆本身。
如下图中的红色圆:
如果
,则此时 就是单位圆。
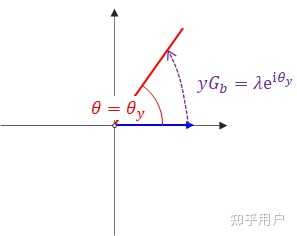
同理,我们可以找出一个右陪集:
由于伸缩变换和旋转变换具有可交换性,因此
另一方面,我们可以看出,
这样,我们也可以同样构造
直观理解:
它的几何意义,是将实轴上的向量变成倾角为的 射线 上的任一点的所有变换的集合,我们也不妨直接将它视为倾角为 的射线本身。
如下图中的红色射线:
如果
,则此时 就是与正实轴重合的射线。
3) 正规子群的几何直观
群论里说,如果
则称
在本文给出的例子中,显然
直观理解:
这个例子的几何意义相对来说比较无聊:
经过共轭变换后仍然是它自身,也就是单位圆先后经过一次 倍和一次 倍的缩放后,还是单位圆; 经过共轭变换后仍然是它自身,也就是正实轴上的射线先后经过一次 角和 的旋转后,又回到了正实轴上。
4) 商群的几何直观
根据商群的定义,如果
这是我学习群论时曾经感到最困惑的概念之一,所幸当我构造出本文这个例子时,发现可以从中窥视商群的一些几何意义。
从定义我们可以看出,商群
回到我们的例子,
那么这个商群的几何意义是什么呢?
直观理解:
根据前面讨论的左陪集的几何意义,我们不妨做这样的类比:
商群在几何上就对应着复平面上所有同心圆之间的旋转加伸缩变换的集合,但由于圆在旋转变换下不变( ),因此实际作用下来只造成伸缩变换( 于是每两个同心圆之间的伸缩变换就对应着 的一个群元及其逆元 ),即:
> 群乘法就是两次伸缩变换的叠加,即: 式
式
另一方面,
直观理解:
根据前面讨论的左陪集的几何意义,我们也可以做出这样的类比:
商群在几何上就对应着复平面上所有从原点出发的射线( 不包含原点 )之间的旋转加伸缩变换的集合,但由于射线在伸缩变换下不变( ),因此实际作用下来只造成旋转变换( 每两条射线之间的旋转变换就对应着 的一个群元及其逆元 ),即:
式
群乘法就是两次旋转变换的叠加,即:
式
5) 直积的几何直观
根据群直积的定义:
我们可以发现,群
而联想到前面讨论的群
直观理解:
根据前面的类比,群是旋转变换、几何上对应着单位圆,群 是伸缩变换,几何上对应着与正实轴重合的射线,于是两者的直积就可以从两个视角去理解:
- 将单位圆进行伸缩,覆盖整个除原点外的复平面( 后文简称“空心复平面” );
- 将正实轴的射线进行旋转,也覆盖整个空心复平面。
无论哪种,最终得到的都是整个空心复平面,这正好也就是群覆盖的区域,所以我们不妨将这个直积理解为“一条线扫完整个复平面”的过程。
另外,我们注意到,积和商是一对互逆的运算,因此直观上我们难免会产生这样的联想:
是否也可以看成 “除以” 后得到的“商”?( 反之亦然 )
但我们前面已经定义了商群,而商群是陪集的集合构成的群,并不是的子群,所以这似乎和直觉矛盾了。
不过没关系,马上我们会看到,和商群 其实是同构的( 毕竟它们的几何意义都是伸缩变换 ),并且,几何上商群 可以理解为空心复平面 “除以”同心圆后剩下的“伸缩”的动作,这和空心复平面 “除以”同心圆 后得到的那条射线 的确是可以对应的。
6) 同态与同构的几何直观
我们先来说同态。
如果用一句话简单概括同态,就是:
同态映射就像是茶壶配茶杯的关系。——辜鸿铭

我们把这句话再说得更具体一点,并且加上群结构,就可以凑出同态的定义来:
假设有
- 所有茶壶构成一个群,记作
- 一把茶壶固定搭配
- 映射
- 映射
那么群
另外,如果茶杯
上面说的例子是离散的,现在我们回到本文开头给出的连续群的例子。
很明显,群
且保留了群乘法:
而这个同态映射的核显然就是
结果我们发现,这个同态核居然就是伸缩群
接下来说说这个同态核的几何意义。
直观理解:
我们发现,群到群 的同态映射 其实等于是将空心复平面上的点全部投影到了单位圆上,这样, 中的长度伸缩的信息就被舍弃了;
而这个同态映射的核的几何意义也就很明显了:它就代表同态映射中丢失的长度伸缩信息。
所以在我们的例子中,同态映射其实相当于一次降维操作,被压缩的那个“维度”,就是同态映射的核。
另一方面,我们在到群 之间也可以构造一个同态映射,此时是旋转的信息被抹去,空心复平面上的点全部降维到正实轴的射线上,而同态核就是降维时丢失的旋转信息 > 这其中的微妙关系实在值得玩味……
接下来我们来说同构。
理解了同态之后,同构映射理解起来就简单多了,只要把同态的一对多变成一对一,同态映射就变成了同构映射。
同态是一夫多妻的旧社会,同构是一夫一妻的新社会。
在我们的例子中,群
这个映射的逆映射也是唯一的:
它们显然也是满射( 各自覆盖了群参数的定义域 ),并且保留了群乘法:
所以这就是一个同构映射。
不过这个映射并不是我们想讨论的重点,接下来我们要来讨论一个更有意思的同构映射,就是前面提到的商群
这个同构映射其实十分显然:
(
( 注意:映射的左边虽然有无穷多个
直观理解:
商群与子群 之间的同构关系意味着,单位圆的缩放可以“降维”成正实轴上的向量的缩放,两种缩放本质上是可以等同的,仅仅是它们的作用对象不同而已。
另一方面,在
这样,我们也就将商群和直积群之间的关系联系起来了。
而这种同构关系其实也可以看成著名的 群同态基本定理 的一个案例:
若
是一个群同态,记 ,则 > ( 表示同构关系 )
数形结合如此完美。
本回答改编自学习笔记:
( 笔记内容与本回答高度重合,不用重复观看 )
评论:
低级群论:
例子不行哦!
比如,同态,
是压缩群的意思,一个群A,30个元素,找一个子群B,5个元素,把原来的群分成6组,又是一个群C(商群),
为什么叫商群?
因为A必然有个子群D,同构于C,
A=B×D。这不就是商吗? (6 🤍)
PeiLingX: 谢谢指点,我再重新想一下🤔 (1 🤍)
abada张宏兵:
爱学习的祖国好少年: 😲可以问一下这篇笔记是配哪本书的呢? (5 🤍)
PeiLingX:
我是几本书同时看的,按我阅读的细致程度排序的话是这样的:
1. 《Group Theory in a Nutshell for Physicists》(徐一鸿);
2. 《物理学中的群论基础》(A. W. Joshi);
3. 《An Introduction to Tensors and Group Theory for Physicists》(N. Jeevanjee);
4. 《Group Theory in Physics》(董无极) (5 🤍)
爱学习的祖国好少年 -> PeiLingX: 😳谢谢 (1 🤍)
嘿嘿 -> PeiLingX: e
沉舟: 请问可以帮忙做群论作业吗 (5 🤍)
好奇量子力学的人: 你想多了🤭🤭🤭 (3 🤍)
户部: 可不可以这么理解,群是一种封结妖逆的变换,是一种变换效果可叠加(封闭性)、变换顺序无所谓(结合律)、可做什么都不变的变换(幺元)、变了也可以变回来(逆元)的变换。 (2 🤍)
知乎用户01IrSp: 👍好通俗易懂
abada张宏兵:
Eagerming: 同态映射核定义处,茶壶和茶杯貌似说法了。即下面这句话的茶杯和茶壶应该对调:“如果茶杯 [公式] 是茶杯群中的幺元,那么它对应的茶壶的集合 [公式] 可以构成茶壶群的一个子群(证明略 ),这个子群被称为同态映射核,记作 [公式]”。个人理解 (1 🤍)
昌哥: 陪集说的真好
willgoon:
这样的乘法本身就是“畸形”的,因为它无法定义唯一的“连续操作”。
请问什么叫做唯一的“连续操作”?
沁姬存希: 夹带私货
蒸汽芥末: 石头剪刀布老演员了[吃瓜],它还可以是满足自反性和反对称性、但不可传递的经典反例