复数的物理意义是什么？ - Heinrich 的回答

在信号与系统 复数信号 物理意义中有问题的详细解说，但由于我是学物理的，所以对其解释不是很明白，希望可以从物理的角度去理解，如果能结合电磁波传播的波动方程解说是最好不过了

数学, 物理学, 复数（数学）

这个必须回答！

复数最直观的理解就是旋转！

4*i*i = -4 就是“4”在数轴上旋转了180度。

那么4*i就是旋转了90度。

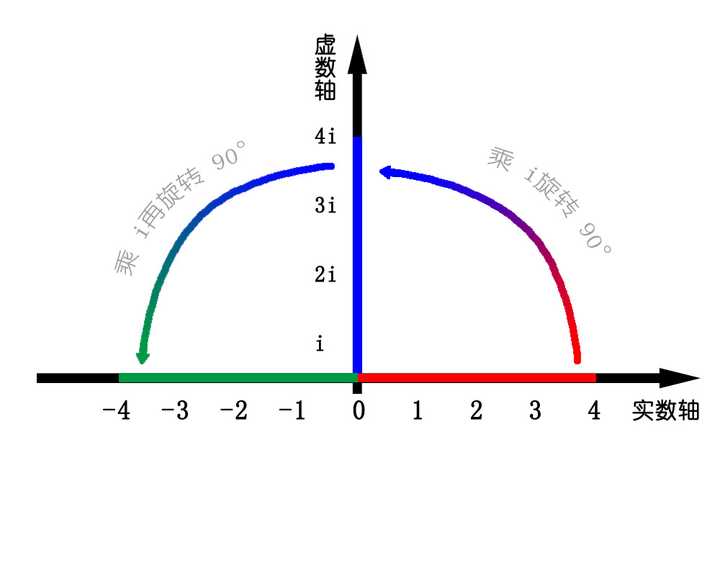
另外，e^t是什么样呢？

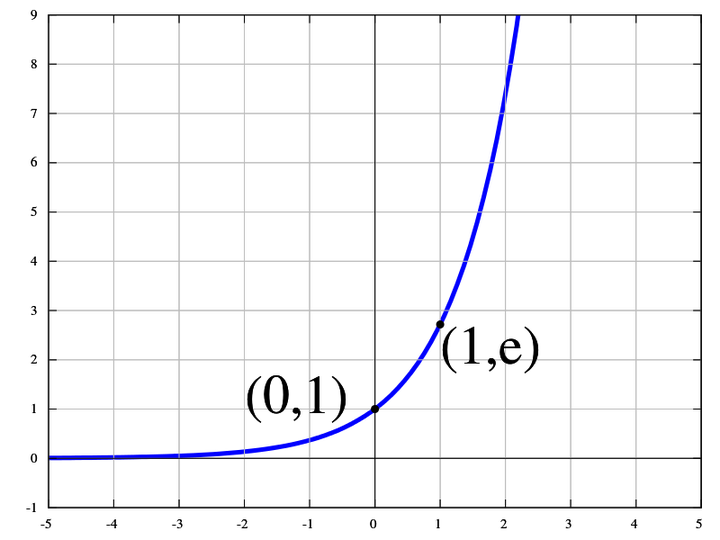
但当你在指数上加上i之后呢？

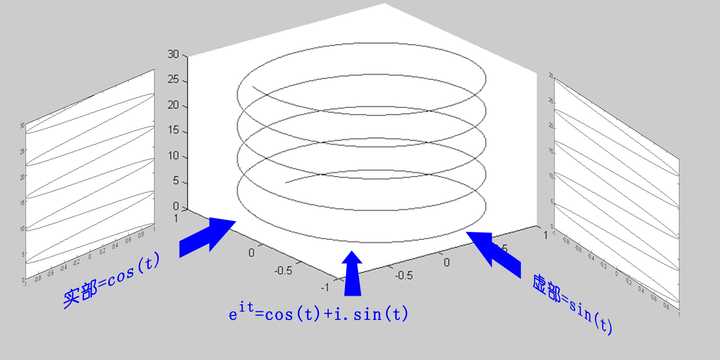
变成了一个螺旋线。是不是和电磁场很像？（想拿欧拉公式去跟女生炫学术的男生注意了：她们，真的，不CARE）

当然，更重要的意义在于复数运算保留了二维信息。

假如我让你计算3+5，虽然你可以轻松的计算出8，但是如果让你分解8你会有无数种分解的方法，3和5原始在各自维度上的信息被覆盖了。

但是计算3+5i的话，你依然可以分解出实部和虚部，就像上图那样。

基于以上两个理由，用复数来描述电场与磁场简直完美到爆棚！

我们即可以让电场强度与复数磁场强度相加而不损失各自的信息，又满足了电场与磁场90度垂直的要求。另外，一旦我们需要让任何一个场旋转90度，只要乘一个“i”就可以了

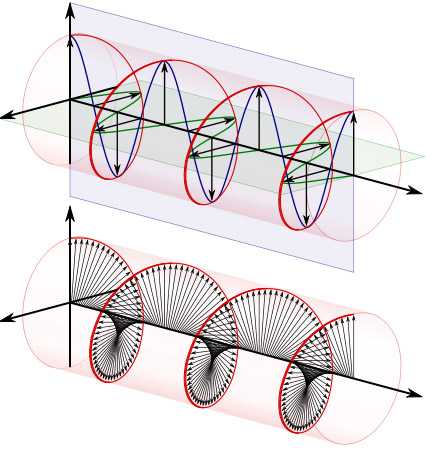
受 @physixfan 答案的提醒，再补充一点。

正弦波在频域可以看作是自然数中的“1”，可以构成其他数字的基础元素。当你需要5的时候，你可以看成是1*5（基础元素的五倍）也看以看成2+3（一个基础元素2倍与基础元素3倍的和）。这些用基础元素构成新元素的运算是线性运算。

但是现在你如何用线性运算吧2sin(wt)变换成4sin(wt+pi/6)呢？

利用欧拉公式，我们可以将任何一个正弦波看作其在实轴上的投影。假如两个不同的正弦波，可以用数学表达为：

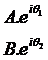
好了，现在如果我想用第一个正弦波利用线性变换为第二个，我们就只需要将A乘对应的系数使其放大至B（本例为乘2），然后将θ1加上一定的角度使其变为θ2（本例为加30度），然后将得到的第二个虚数重新投影回实轴，就完成了在实数中完全无法做到的变换。

这种利用复指数来计算正弦波的方法也对电磁波极其适用，因为电磁波都是正弦波，当我们需要一个电磁波在时间上延迟/提前，或是在空间上前移/后移，只需要乘一个复指数就可以完成对相位的调整了。

（图1图3系自制，转载不注明出处注定一辈子学理工没女朋友）

题主关注我的专栏吧，近期会写科普傅里叶的东西……

知乎用户: 学习了，课堂上老师只教怎么解题，这些根本不讲 (95 赞)

Heinrich -> 杉哥: 偷偷表示这些我们老师也不讲都是课下自己琢磨出来的会不会被说成是装(哔)…… (73 赞)

赵哈哈 -> Heinrich: 太厉害了！👍 (2 赞)

天地间一远行客 -> 杉哥: 高中课堂上曾经讲了，被学生质问，这个高考考吗？不考讲这个干什么？

秋天 -> 杉哥: 因为大多数老师自己也不懂 (8 赞)

蓝孩儿 -> 杉哥: 老师的信息量也有限啊，他们只负责知识灌输和以提分为关注点。至于未来你们如何见解，他才没心思呢[调皮] (1 赞)

冰蓝的水晶 -> 天地间一远行客: 不让讲的学生是否有人教了，然后不想让别人也懂？

天地间一远行客 -> 冰蓝的水晶: 他们不懂，且没有兴趣知道 (1 赞)

知乎用户:

這個好！

我強烈地說，能不能把這個想法更豐滿些，給更多例子，一些更複雜的強有力的例子來說明這件事。

我覺得複數的最大物理內涵，在具有 因果關係的 Lorentzian 場論 和具有溫度信息的Euclidean 場論 這二者的鏈接上。在後者的場論中，
也有類似你上面提及的“螺旋” 週期。 (81 赞)

阿喨 -> 知乎用户: 这2个里是怎么会出现复数的呢？

梁晓东:

看过大神的文章，的确非常值得我们阅读，深入浅出，容易理解，但在实数指数到复数指数的图像转换时候，总是想不明白是怎么变化成螺旋形的，后面通过其他资料算是理解了，这里分享一下：在复数平面，点可以表示成a+bj的形式，j^2=-1，如果用极坐标形式表示则有a

• jb = M (cosθ + j sinθ) ，这里M=根号（a^2+b^2），θ是a+bj在复平面的夹角，θ=arctan（b/a），这样a=M
  cosθ ，b = Msinθ，而有上面的表达式，根据泰勒级数，cosθ + j sinθ=e^(jθ)，所以a + jb
  =Me^(j*θ)，这里结合大神的式子，由于角度是有周期性，t变量的变化其实是θ的变化，所以会有螺旋形曲线出现。希望可以帮助到大家理解，谢谢 (60 赞) 科研儿童 -> 梁晓东: 厉害了兄弟，谢谢你的分享
  

陌归: 看过之后表示数学物理方法白学了……•﹏• (57 赞)

终不似少年游 -> 陌归: 复变函数里有讲啊，复数的模与俯角 (5 赞)

知乎用户: 太感谢了。如果你来写教材，实国人之幸！ (40 赞)

张苏: 写傅立叶的东西 能不能我和您合作 或者我给打个下手 我也很感兴趣啊 (32 赞)

Heinrich -> 张苏: 好啊好啊，私信聊吧，不过今天有点晚，我得睡了，明天详谈吧。（睡觉前就不该手贱刷知乎，回答完这个问题现在都两点半了……） (73 赞)

小豆丁 -> Heinrich: 你的签名让我很伤心啊…

知乎用户: 用力学的概念来说，加和乘法是平移和变形，复数就是增添旋转这个保证完备性的自由度。 (23 赞)

Wade Hisung: 学电气的表示看懂这些毫无压力。非常感谢提供了新的角度。 (17 赞)

St Jason:

假如我让你计算3+5，虽然你可以轻松的计算出8，但是如果让你分解8你会有无数种分解的方法，3和5原始在各自维度上的信息被覆盖了。
但是计算3+5i的话，你依然可以分解出实部和虚部，就像上图那样。

这个比喻我认为不恰当，我认为这样理解，比如值为8的数，可能是8，可能是8i，可能是8exp(3pii)，那么8，仅仅是许多个值为8的数其中一个，所以，复数拓展了数表示方法。
如你所说，复数意义是旋转，那么，在涉及到有旋转，有圆的地方，就用复数表达，角度变了，东西就旋转了，而你想如果没有复数，如何表示旋转？实数+角度，比如正余弦，外加一个幅值，那么，除去正余弦，用数，用数字，用数，怎么表示，那么，复数，俺就来了
所以，即使很多人会运算复数，但不理解，我认为要弄懂里面的哈数，就要弄明白复数的内涵。不需要公式，需要理解
只需要想，角度用数怎么表示呢？来吧，复数，然后再来谈运算 (10 赞)

Feeo -> St Jason: 补充的漂亮，你肯定有女朋友了棒 (2 赞)

深蓝 -> St Jason:

线是一维的，而角是二维的，用数表示角那就只能升一个维度。为了升维就要引入二维平移的i，而升了一个维度不仅增加了一个二维平移，还需要二维旋转，所以i^2=-1.
所以复数的根本是维度的增加。而微分又是升维的，又有了拉普拉斯算子 S=jw. .... 复数和微积分又扯上了关系。。。
数圈关系太复杂，远的近的都貌似能有一腿，哈哈😱😱 (11 赞)

夏红: 亲 作为一个女理工生 最崇拜你这种把复杂的数学知识讲解的很形象的大神，为你打call 你最帅 (7 赞)

from: https://api.zhihu.com/appview/api/v4/answers/26017000