线性代数的角度重新理解行列式 - 知乎

线性代数, 行列式, 朱元, 无专栏

行列式的本质是什么？

曾经在知乎的这个回答里，我尝试用一种通用的学习新知识的角度来告诉大家如何去 开始 理解行列式，但是对于大部分人来说似乎显得不必要，也过于生涩和不切中要害。

事实上，大部分人的问题不是在于第一次看行列式看不懂或不理解它的定义，而是学完了整本线性代数之后不知道行列式的作用和本质是啥：多数教材认为我们中的绝大多数人在毕业之后 对线性代数知识的最多的使用仅仅是用于解线性方程组，所以教材基本都基于如何又快又好的教你解线性方程组（而且主要是方程数量和未知数数量 相等的方程组）来进行设计：先教行列式，再教克莱姆法则解方程组，再教矩阵，再教逆矩阵、矩阵初等变换、高斯消去等方法解方程组（数清楚茴字有多数种写法了么？手算版，矩阵版，可计算机编程求解版～～）～～整个课程主线就是4个大字： 解方程组。 线性代数课程可以做到前半学期甚至整个学期的每一节课程都不偏离这个主旨来给你灌输各种花式解方程组的技巧。

这种扭曲的路线不仅让人容易误解“线性代数”这4个字就是一门讲“线性方程组”的课程，而且稍微有一点外溢的知识扩展立即就容易让人懵逼：相似矩阵？双线性映射？这些东西是做啥的？ 雅可比矩阵？居然还微分？笔者本科毕业2年之内，离这门课程结业已达4年，更不要说中学时代就看过这些书，对这几个概念的懵圈感依然非常强烈，距今依然记得大学自从线性代数这门课开始起，就无法做到对所有课堂知识完全 融会贯通 。间接也影响了笔者后面学习复变函数，信号处理（傅立叶变换是继线性代数之后笔者第二个在大学学堂没完全搞清楚整个数学模型 意义何在的玩意儿 ）等课程内容的积极性：那时候的自己终于选择认输，，原来自己也不是能掌握人类所有知识的那种人啊。

直到后来的科研和工作需要不少抽象代数的知识，逼着自己重新拾起线性代数的很多基础概念。尤其是读研期间有一次导师让我改本科生线性代数课卷子，逼着自己重新回到象牙塔重新苦读，终于好好理解透了很多基本概念定义的来历，对于自身的认知提升和科研能力的培养也起到了巨大的作用。

回到我们的题目：行列式在线性代数这个学科中到底起到什么作用？如果只是解方程中的一个子表达式，为什么教材把它单独拧出来大讲特讲（在我中学看这一部分介绍的时候，我真的不觉得行列式比二次方程求根式中的判别式更重要，虽然二者都是求解方程解的一个重要子表达式，可以用于判决解的存在性、性质、数量）？甚至在很多本科线性代数教材里第一章就如同天(e)神(mo)下(jiang)凡(shi)的引入了 置换和逆序数 这样抽象的概念，就为讲解一个行列式？要知道讲这些内容的时候，绝大多数课程设计甚至连离散数学这样的课程都还没开讲。当年的阴影让我在以后学习抽象代数甚至写paper选择术语的时候依然对“置换” 这个概念非常厌恶。

本文并不尝试回答以上所有的问题（虽然笔者的情绪让自己忍不住吐槽一下过去10多年的认知歧途），这超出了本文的范畴。我推荐阅读本文以下内容的同学尤其是对线性代数课程本身未必是还很熟悉的同学先看看 B站3Blue1Brown 线性代数学习视频

https://www.bilibili.com/video/BV1ys411472E?p=10

来做一个热身。这份视频系列假设你已经学过了线性代数，然后重新用一种偏向几何的角度和顺序讲解我们那些课程中出现的角色，配合现代编程软件很直观的用网格动图描述了空间变换下空间的点和线的线性运动或线性拉伸与旋转、翻转：首先讲线性空间、线性变换，再把这些东西建模而给出矩阵和矩阵乘法的概念。接下来 才 讲行列式。这种先讲矩阵再讲行列式的介绍方法得到了绝大多数观众的好评，普遍认为这让很多概念的理解变得容易了许多：至少把行列式介绍为对单位基向量组进行线性变换的尺度缩放因子，绝对比把它介绍为方程组解的子表达式要形象好多。

然而它的这种讲解顺序里依然没有讲出来这个问题的答案：行列式为什么表达式长成这个怪样子？视频作者简单的用了一系列图示进行了讲解，然而其实依然是不直观的，充斥了各种硬算出来的结果的。并且视频作者不认为这和线性代数视频的核心本质相关

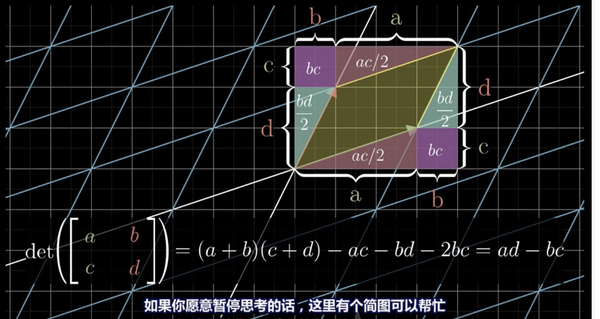
然而笔者认为这个视频序列其实应该把点积和叉积的前半部介绍提前到行列式之前，这样可以比较简单的把行列式的几何意义与代数表示进行结合，而且对于大学课程而言本身也能和高中立体几何课程更紧密的结合。我相信看完本文内容并深入思考的读者未必赞同行列式的展开计算和线性代数的本质无关。

笔者并不尝试在这里讲解多线性映射的概念来引出行列式表达式。相反，笔者希望能够通过自己的语言和组织，来让读者能自己对这个问题背后的更多细节产生兴趣。笔者以上花了很大的篇幅来铺垫这个问题的背景，也旨在唤起读者对很多也许有些遥远的线性代数知识的 兴趣 ，否则没有兴趣的情况下，即使本文也未必是很好理解的。

线性代数课程里有一个非常让人难以理解的事情是：外积，又称叉乘、叉积，这个概念为何只适用于3维向量空间？高维不行么？2维不行么？线性代数不应该是所有知识都类似内积适用于所有维度的么？ 高中我们学过法拉第定律，一看外积的右手定则就猜到2者有关系，混合积又是什么鬼？？感应电磁力做的功？ 外积和混合积的计算方法为啥和行列式那么像 ？

我也不卖关子了：

1. 点乘是一种把一个多维向量映射到一个零维的数的线性映射函数。例如(a, b).(x, y)=ax+by, 我们把这看成一个针对2维向量(x,y)的映射为一个数的函数。
2. 现在我有一个向量(x, y)，我希望把它映射为以它为边的一个以原点为端点的平行四边形的面积（这也是一种把向量映射为数的过程，先忽略单位）。设平行四边形另外一个过原点边为向量(a, b). 请问这个面积映射函数S(x, y)该怎么写呢(可以暂时先忽略符号)？

不假思索的，可以很粗暴的写出来S(x, y)=bx-ay. 也就是行列式 。但是我们希望能够辅助以线性代数的方法来解释这个答案。

我们知道(x, y).(a, b)=ax+by, 和S(x, y)的表达式有些像但并不是。现在我们设法需要找出来S(x, y)是什么内积表达式。毫无疑问 S(x, y)=(x, y).(b, -a)。那么(b, -a) 和(a, b)是什么关系呢？

没有关系我们可以定义它们有关系：我们定义(b, -a) 是(a, b)的 “外积”！！！

我疯了么？不没有，我没有尝试篡夺教材撰写者作为数学定义颁布者的权限。接下来我们会解释这样的定义非常自然。我们引入一个符号O表示 外积 ， 。注意它并不固定只接收一个向量，接下来大家会看到：外积符号O接收一个或多个向量，但只输出一个向量。

我们知道平行四边形的面积计算方式是邻接两边长度的乘积再乘以夹角的正弦. 但是我们的任务是用内积来表达这个面积，而内积明明是乘以夹角余弦的，怎么办？

，是(a, b)的-90度旋转！！（即顺时针转90度，我们假定逆时针旋转为正方向）。设(a, b)和(x, y)的夹角为 , 我们把(a, b)向量旋转-90度得到(b, -a)，(b, -a)和和(x, y)的夹角为 。再利用 咱们就可以用向量内积来表达那个平行四边形面积公式了：以2个向量为边的平行四边形的面积是一个向量的外积 再内积另外一个向量。即 S(x, y)=(x, y).(b, -a)=(x, y). O((a,b))= 。

等等，先外积，再内积，这不就是，是不是有点像传说中的混合积？我们在二维里搞出来了这个。。

让我们迈入三维空间的殿堂：

端点在原点的平行六面体的体积，等于是过原点3个边所在向量构成的行列式的结果。

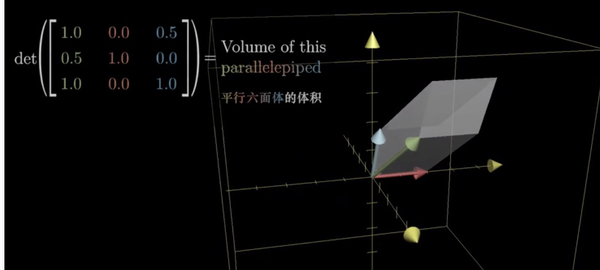
借用3Blue1Brown 在 https://www.bilibili.com/video/BV1ys411472E?p=7 中的图示

我们继续使用上文中的流程：

现在我有一个向量(x, y, z)，我希望把它映射为以它为边的一个以原点为端点的平行六面体的体积（这还是一种把向量映射为数的过程，先忽略单位）。设平行六面体另外2个过边为向量(a, b, c), (d, e, f). 请问这个体积映射函数S(x, y, z)该怎么写呢(可以暂时先忽略符号)？

不假思索的，可以很粗暴的写出来S(x, y, z)= =x(bf-ec)-y(af-dc)+z(ae-bd)。但是我们希望能够辅助以线性代数的方法来解释这个答案。

把S(x, y, z)写为内积表达式S(x, y, z)=(x, y, z).(bf-ec, -(af-dc), ae-bd)。那么(bf-ec, -(af-dc), ae-bd) 和 (a, b, c), (d, e, f)是什么关系呢？

聪慧如你一定发现(bf-ec, -(af-dc), ae-bd)就是写在咱们教科书里的三维变量(a, b, c), (d, e, f)进行外积或 叉积 的结果向量的定义。为了符号的一致性，我们继续”自定义“外积：

O((a, b, c), (d, e, f)) = (bf-ec, -(af-dc), ae-bd).

我们继续玩弄上面的几何方法来对外积进行解释：

平行六面体的体积等于(x,y,z) 的长度乘以(a,b,c), (d,e,f)所围成的平行四边形的面积再乘以 (x,y,z) 和(a,b,c), (d,e,f)所在平面夹角的 正弦。联想到我们上面把正弦变成内积所需要的余弦的方法，利用(x,y,z) 和平面夹角的正弦等于和平面法向量夹角的余弦，我们就只需要证明(bf-ec, -(af-dc), ae-bd) 长度是(a,b,c), (d,e,f)所围成的平行四边形的面积，而方向垂直于(a,b,c), (d,e,f)所在平面（只需证明和它们2个向量都垂直即可）。

这两个待证明点本身就意味着一些很重要的结论：

1. u=k(bf-ec), v=-k(af-dc), w=k(ae-bd) 是方程组au+bv+cw=0, du+ev+fw=0的一组通解

这其实就是(u,v,w) 和(a,b,c), (d,e,f)所在平面垂直的意思。如果(a,b,c), (d,e,f)线性无关（才能围成平行四边形），这组通解也就唯一。

2. (a,b,c), (d,e,f)所围成的平行四边形的面积为
3. u+v+w= ， k=1时，向量(u, v, w)的长度和u+v+w相等，也等于(a,b,c), (d,e,f)所围成的平行四边形的面积。