如何通俗易懂地解释「协方差」与「相关系数」的概念？ - 傅渥成 的回答

其背后的原理为何可以达到衡量「相关性」的效果？

数学, 统计学, 数据分析, 傅渥成

看到这个问题，马上想到我那天回答的另一个问题了。我们在刻画这个世界之间的各种关系的时候，常常会希望度量“距离”：

1. 对于空间中的两个点，我们可以用勾股定理定义平方和作为距离；

2. 对于两个二进制序列，或者两段基因序列，我们可以用汉明距离来度量二者之间的差异，作为“距离”；

3. 那么假如对于两个复杂的量（描述这两个量可能用很多很多的参数），那么这时候怎样度量二者之间的“相关性”呢？

按照真正的逻辑顺序来讲，应该是这样讲的：

把所有的这些复杂的参数排成一列，就拍成了一个向量，很多很多的这样的向量构成了一个向量空间。向量空间里面的东西没有“距离”这样的概念，对于一个向量空间里面的向量，甚至没有“长度”这样的概念，因为向量空间只是一个代数结构，没有度量或者拓扑的概念在其中，那这时候怎样度量向量的长度来呢？接下来，又怎样来确定两个向量之间的“距离”呢？

对于一个可以定义距离的结构（

度量空间

），我们需要有一些要求，认为满足这些要求的一个函数就可以认为是距离，例如我们要求：A到B的距离等于B到A的距离，A到A的距离等于0，两个点之间的距离非负，三角不等式。那么对于一个向量空间，怎样可以最自然地给它一个“范数”，使得它有可能推广到一个距离空间（度量空间）呢？最自然的方法就是引入“内积”的概念了，通过内积的运算，得到

内积空间

，再用内积来定义距离（范数），于是也就有可能得到距离空间。

为什么内积空间可以变成一个度量空间呢？这就是我在“

学一门课的时候，要注意理解和思考，不要一味的背公式，背习题是什么意思？

”这个问题里面，我反复用到了 Cauchy 不等式，目的也正在此。Cauchy 不等式为我们提供了判断两个向量是否相关的方案：( a ・ b )/| a || b | 可以作为度量相关性的一个函数，而它的直观意义是什么，请看下面。

—————————————这是一条分割线——————————————

好了，截止到目前，都是我认为一个比较正常，且不算太难的一种解释的方法，如果觉得这样理解起来还有困难，那么接下来就只能用能让中学生听懂的，最直观的方法了，但是我并不喜欢这样直观的讲法，因为这个讲法的逻辑是很混乱的，事先就引入了很多不应该过早引入的概念，不过为了帮助理解，也就这样吧：

• 有两个向量，我们希望定义它们是不是相关。一个很自然的想法，用向量与向量的夹角来作为距离的定义，夹角小，就距离小，夹角大，就距离大。

• 但是怎样来计算夹角呢？为了让这种计算可行，我们要选一种恰当的三角函数来算。

• 正弦函数的不太好的一个原因是因为加上个90°，正弦算出来得到的结果一样，而两个向量的夹角是30°还是120°这是完全的两码事，此外，正弦函数也不适合推广到高维度向量的计算中的“两两比较”。

• 那么考虑用余弦吧，这个可以很方便地区分30°和120°，而且还有一个好处——余弦的计算非常简单，用内积就可以计算了，中学数学中就学过： (x1,y1)・(x2,y2)=x1x2+y1y2，这就是内积，你要是喜欢，也可以把这个叫做“协方差”。

• 但是这个内积的定义很奇怪哎？要是两个向量本身就长，那这个也算不出夹角来，所以再要除以两个向量本身的长度，即，夹角：cos < a , b > =( a ・ b )/| a || b |;

• 这样，那么两个量是不是相关，怎么来判断？就用余弦的大小就可以了，我们把两个向量的夹角的余弦，就叫做“相关系数”，正如上面的式子所指出的，写开了就是：
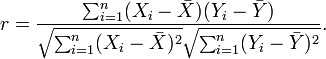
  分子上面的就是一个内积的计算，也就是前面我说的“协方差”，分子下面是两个勾股定理乘起来，是两个向量的长度。如果两个向量平行，则它们夹角的余弦（也就是“相关系数”）就等于1或者-1，同向的时候是1，反向的时候就是-1。如果两个向量垂直，则夹角的余弦就等于0，说明二者不相关。

• 再写我都不好意思了，我觉得这样应该很容易就可以懂了……

王赟 Maigo: 30度和120度的正弦不会混的，会混的是30度和150度 (26 赞)

知乎用户 -> 王赟 Maigo: 对，是这样~

鸭鸭鸭 -> 知乎用户: 没搞清楚事情的高光点

盗跖庄屩流誉后: 傅老师您好，您的答案通过与线性相关的类比，使我建立起了协方差的直观形象，但我还是有一个疑问，为什么人们用“内积”来刻画表示离散程度的方差呢？数学期望（均值）在这里是不是起了“原点”的作用？ (13 赞)

傅渥成 -> 盗跖庄屩流誉后: 是的 (1 赞)

盗跖庄屩流誉后 -> 傅渥成: 谢谢老师。 (2 赞)

碎叶城c -> 傅渥成: 👍很喜欢这种不同学科知识点的串联，对我两门学科的理解都很有帮助😝

流沙: 概率论中的概念居然用线性代数来解释，是我理解错了，还是发现了概率论和线代的交点？求答主多讲一点！ (9 赞)

傅渥成 -> 流沙: 不是什么“发现交点”，这些就是一码事啊。 (11 赞)

流沙 -> 傅渥成: 作为一名考研党，我正在复习（其实是预习）概率论与数理统计，搜索协方差和相关系数发现了你的回答。可貌似是用线性代数中向量空间的概念解释的，从没想到它们有什么联系。（线性代数我也只复习了前六章要考的）。可能是我数学知识太少了。有种盲人摸象的感觉。现在怀疑我数学是跟语文老师学的。 (3 赞)

傅渥成 -> 流沙:

你看看它们的长相，都是一个内积（形如
a1b1+a2b2）除以长度的积（形如sqrt(a1^2+a2^2)），这就是中学学过的余弦的定义，所以其实都是在看一个夹角，夹角为0或者180°，则二者相关，夹角为90°则二者不相关。这些都应该是高中就可以理解的东西，你不用想得太复杂。 (8 赞)

毛毛 -> 流沙: 2017考研党也看到了

眉间纸 -> 傅渥成: 本来就是一码事，真的

东方盛夏 -> 流沙: 可以参看矩阵分析与应用这本书，在信号处理中矩阵论和概率论是结合使用的，更准确的说，数学本身就不分家 (1 赞)

鸭鸭鸭 -> 傅渥成: 太强了，醍醐灌顶，顿悟了

LeslieXong: 非常感谢。 有个小疑问， 此处向量变成了减去均值的X，Y向量了，按照这个理解的话为什么不直接用原X，Y向量做内积除以向量长度呢？ (5 赞)

知乎用户JabUAi -> 盗跖庄屩流誉后: 不能理解，能否请您解释下

lee -> LeslieXong: 如果直接用X、Y向量，那么r就是衡量X、Y是不是同时偏离0向量了，这与衡量X、Y是否同时偏离各自的期望是两码事。相关系数衡量的是后者 (4 赞)

丁力 -> LeslieXong: 同问

斯莱姆蛋壳 -> LeslieXong: 我和你有同样的疑问，请问你想明白了吗？？

徐杨 -> 斯莱姆蛋壳:

可以这么理解 向量是指从原点指向的那个点 中心化的意思是 将所有数据平移 使之均值为0 从而两个向量的内积就是指协方差 如果进行标准化 内积就是相关系数
协方差本质就是数据做中心化之后的内积 相关系数就是数据标准化的内积 (7 赞)

斯莱姆蛋壳 -> 徐杨: 感谢帮助，谢谢！

三十年刺蜜 -> 徐杨: 说得太好了！

Kaiwen Sun:

谢谢学长（大物被你TA过）！看过那个r的式子后我还有点疑问：我一开始把Xi和X-
bar都误以为成了向量，所以觉得在X的向量空间中对所有Xi减去向量的均值似乎是有道理的。但仔细一想，觉得不太对：每一个Xi是随机变量的X（标量）的一次采样，对应着X向量空间中的一个维度。所有的Xi排成一排，构成了向量空间中的【一个】向量。从向量的角度来考虑，为什么要把这一个向量的各个分量上都减去所有分量的平均值？ (3 赞)

ccsplendid -> Kaiwen Sun: 因为是要算出每一个样本和期望的偏差

Kaiwen Sun -> ccsplendid: 谢谢！但是从向量的角度来考虑，为什么要这样减呢？

Ramkk -> Kaiwen Sun: 是先向量标准化后，再做的夹角计算。具体来说，首先有向量X=(x1...xn)，但是这个向量每个维度的度量方式可能相差很大，（比如x1代表房间数目：最多取到5，x2代表价格：可能几十万）所以将向量X标准化后，用a代替。a=(X-EX)/sqrt(DX)，此时a的长度为1；同理对Y也做相同的处理，b=(Y-EY)/sqrt(DY)。最后算ab的夹角。

Kaiwen Sun -> Ramkk:

谢谢您的回复。我一开始与您的想法一样，也是人为这是在做标准化。但仔细想想觉得不对。
按照二维坐标系XOY中余弦的定义，对于向量a=(xa,ya),
b=(xb,yb)，二者的余弦为cos=a•b/(|a||b|)=(xaxb+yayb)/sqrt(xa^2+ya^2)sqrt(xb^2+yb^2)。
对比傅渥成在原答案中左侧为r的那个式子（称为r式），r式所描述的是一个n维坐标系中两个向量的余弦。注意，这里只有两个向量。我们称其为向量A和向量B，比如n维向量A的第i维分量为(Xi-
Xbar)。
再从随机变量协方差的角度看r式，向量A的n个分量Xi-
Xbar是由n个独立同分布的随机变量产生的。既然独立同分布，也就意味向量A的各个分量是“地位平等”，是单位统一的，不存在(X1-Xbar)的单位是房间数目而(X2-Xbar)的单位是万元的情况，不存在你说的“这个向量每个维度的度量方式可能相差很大”的情况，因而也就不需要做标准化。
如果说做标准化，那我只看出r式是在对可大可小的n做标准化，看不出为什么要在Xi上减去Xbar。
所以，我还是不明白，作为随机变量的协方差的r式在从向量余弦的角度来看时，为什么要写成减去Xbar这样。

顺便再次请求@傅渥成 学长解答 (2 赞)

邪恶总督 -> Kaiwen Sun:

1.n维向量A的i维分量应该是 Xi-Xi_bar，因为Xi也是n维向量；
2.随机变量协方差的定义中并没有要求两个随机变量都是独立同分布的。想法，相关系数即随机变量除以两个随机变量的标准差之积，如果为0的话才是两个随机变量独立的必要不充分条件;
3.协方差关心的只是两个随机变量，对于高维情形，引入了随机向量，协方差阵的概念，这应该是类比的方向。也就是说，我觉得答主的例子举得并不好，举向量的例子是不是一维情形比较好?
4.直观感觉数学期望的期望运算和向量的内积可以构成一个同态映射？

邪恶总督 -> Kaiwen Sun: 应该是协方差矩阵，B=Cov(X,Y),其中X,Y是m维和n维随机向量；协方差阵Var(X)，其中X是n维随机向量，b(i,j)=Cov(Xi,Xj).

响当当 -> Kaiwen Sun: 个人理解，这样做有点“规格化”的意思，把两个向量放到“同一”场合下进行比较，例如x的元素都是大数，y的元素都是小数。

响当当 -> Kaiwen Sun: 另一方面，x,y各自先减均值再除方差，这样有减小数据测量所带来误差的影响，这样算出来的相关性的价值比较高

xcber:

看完了评论，还是没有看到有说服力的解释清楚为什么x,y要减去均值，倒是很多所谓标准化、更准确什么的说法，但是既然答主要从向量的角度解释，向量夹角计算从来没有这种标准化，都是直接按公式算，就算你只看夹角也可以用单位向量『标准化』，而不是用平移来『标准化』.
Intuitive 并不等于 non-technical. (5 赞)

Foulmilk -> xcber:

减去均值是为了消除X无关部分的影响。假设两组变量X和Y不独立，那么我们考虑最简单的模型yi=a+bxi。即使这里向量X（xi）和Y（yi）垂直，由于向量A（a，a，a……）的存在，等式Y=A+bX仍然可以成立，从而造成了“cov=0，而X与Y不独立”，则原命题错误。而考虑ybar和xbar，由于在不独立的情况下ybar=a+bxbar，所以我们将a用ybar和xbar代换，记得到模型为yi-
ybar=b（xi-xbar）。所以如果X与Y不独立，那么对应的是向量Yi-Ybar和Xi-
Xbar内积不垂直（确切说两者共线）。最后强调一点：相互独立变量的cov等于0的逆命题不是对的。 (1 赞)

我家用奥妙 -> Foulmilk: 你这就是瞎扯了，协方差和内积本来就是完全不同的两个东西，理解的角度很新颖，但是完全是错的啊，人家也没说啥别的吧，你这就嘲讽别人没学好。

Foulmilk -> 我家用奥妙: 搞统计的数学都像你这么差吗 (1 赞)

知乎用户: 相关系数类比夹角，方差是内积。受教~ (5 赞)

知乎用户 -> 知乎用户: 协方差是内积，方差是平方和，是距离

Alan: 这个解释有点瞎发挥了。首先，正弦、余弦是三角函数引出的概念，在人类历史上早就出现了，向量还是比较新的概念，向量的内积和余弦的关系是严格推导出来的，不是随便定义的！其次，协方差并不是两个向量之间的内积！很明显，中间还绕一个弯！因为两个向量分别还减去了X拔和Y拔，这其中的几何意义下面回复受教、感谢的人究竟理解了吗？ (2 赞)

高手nba -> Alan: http://m.blog.csdn.net/article/details?id=47656827向量的表示及协方差矩阵，没太看懂，但应该有点关系。

知乎用户 -> Alan:

你大概是高中生只对内积有几何上的理解而没有泛函分析上的理解吧……假设我们有n组观测数据，那么相应就有n个xi和n个yi，那么这就是两个n维向量。那么相对于mean的波动我们也有n个（xi-
xbar）和n个（yi-ybar）——假设记为mi和ni这样就构成了两个新的n维向量。那么协方差的形式就是这两个n维向量的内积（sigma
mi·ni）。所以你的问题大概是既没有看懂这个回答也没有学好高数。 (2 赞)

sarkurai:

"正弦函数的不太好的一个原因是因为加上个90°，正弦算出来得到的结果一样，而两个向量的夹角是30°还是120°这是完全的两码事"
您的数学是体育老师教的么。。rotflmao.. (3 赞)

黄天文: “正弦函数的不太好的一个原因是因为加上个90°，正弦算出来得到的结果一样”，这句有问题，作者修改下吧。 (2 赞)

from: https://api.zhihu.com/appview/api/v4/answers/16393656