关于你转生成为物理学家这档事 - 场论家用几何与代数(第一话):李代数的崛起
title: 场论家用几何与代数(第一话):李代数的崛起
url: https://zhuanlan.zhihu.com/p/344738859
author: 史诗生物 (2d0ae0dc15e175b7000c839729e2e190)
column: 关于你转生成为物理学家这档事 (c_1333798682433945600)
voteup: 369 赞同
created: 2021-01-07 14:13:20
updated: 2021-04-21 18:13:20
fetched: 2022-05-08 16:53:20
count: 约 7074 字
version:
tags: [代数, 李代数, 李群(具有连续的群结构的实流形或者复流形)]
场论家用几何与代数(第一话):李代数的崛起
from 专栏 关于你转生成为物理学家这档事
话题:
代数, 李代数, 李群(具有连续的群结构的实流形或者复流形)
正文:

系列回顾文章的第一话。此系列大致会包含一些代数路线,一些几何路线。代数路线的
- 半单李代数的分类
- 李代数的表示
- 李代数表示的特征标
- 仿射李代数及其表示
- WZW 模型与 Chern-Simons 理论
- 4d
万善之源:李群
在物理中,群是用来刻画对物理系统的「作用」的一种代数结构。这个抽象的结构把下面几个朴素的观点有机地融为一体
- 多次相继作用的效果还是一种作用 (封闭性)
- 作用可以分解成多个作用的复合,不同的分解方法是等价的 (结合律)
- 啥都不干也是一种作用 (有单位元)
- 作用可以被反向作用抵消 (有逆元)
倘若所关心的作用可以通过 连续的参数 进行标记和刻画,那么相应的群就继承了这个“连续”的概念,升级为一个「拓扑群」,不同作用之间有了最粗糙的“近邻关系”或者说“相似度”,我们得以讨论「这个作用跟那个作用相差不大」这样的事情。在物理中,我们往往还可以进一步地要求这些作用对参数的依赖是 光滑 [5] 的 ,那么,此时相应的群就继承了 光滑结构 ,成为了「李群」。相比拓扑群,李群最大的优势就是我们可以 随时随地肆意地讨论“求导” 。
总结起来,李群的定义就是一个「 既是微分流形,又是群 」的东西,并且要求群乘法、取逆操作都要与光滑结构相容 (粗略地说,就是说群乘法、取逆都是无穷阶可导的操作)。
值得指出的是,这种数学对象的定义范式是很常见的,我们往往要求一个东西同时承载、具备多种代数或几何结构 (光滑结构、群结构、线性结构、度量结构,等等),然后下死命令要求所有的这些不同层级的结构要相互协调,以此完成对一个新 (更加精细的) 的对象的定义。
李群非常有趣,但遗憾的是对它的直接研究比较困难。这个困难显然来自两点,一是它的本体,作为微分流形,往往是一个高维、拓扑非平庸、弯曲的空间,二是其代数运算是非线性的运算[6]。
面对如此困难的问题,我们可以选择逃避。逃避可耻但有用,我们可以研究它的简化版问题: 李群的线性化,也就是李代数 。
李代数的崛起
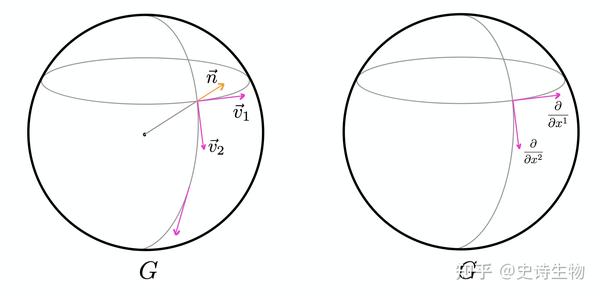
左图是从高维空间的角度看群流形,右边是从内秉角度看群流形
把 弯的对象变直,用直的去逼近弯的对象 ,这是一种古老朴素但非常有效的数学思想[7] 。在微分流形上,我们可以研究 任意一点 处的、沿微分流形方向的 切矢量 ,然后观察这些矢量 沿着微分流形运动时的行为 。当然这句话的潜台词就是“存在不沿微分流形方向的矢量”,也就是采取了“把微分流形放进一个更高维的空间中审视”的古典微分几何观点。这当然是一种可行的视角,不过现代数学家和物理学家更偏向使用“内秉”的观点来研究微分流形,此时,“切矢量”被定义为“对微分流形上的函数的求导操作”——但这又是未来某一个文章的话题了。
不管哪一种视角,切矢量的引入为原本非常“非线性、弯曲的空间”带来了一种 全新的代数结构 :在每一点处,我们有一个由切矢量构成的线性空间,这些切矢量可以做加法和数乘。相比之前,这是一个伟大的飞跃,因为光溜溜的一个微分流形上面什么代数运算都没法做[8]。很多时候,人们把这种思路称为“线性化” (linearization)。这个更加简单、大一的同学就很熟悉的结构为研究微分流形带来极大的便利:只要我们知道各点上的这个线性空间,同时知道这个线性空间如何随着点的移动而变化,那么我们就对这个流形有了深入的了解。
回到李群上。我们的李群是一个微分流形,由许许多多 (无穷多) 个点组成,然后我们希望用线性化的方法来研究它。那我们该在哪一个点做线性化呢?此时,李群的群乘法来帮助我们极大地简化问题:任何一点
综上,我们得到李代数
当我们穷尽所有可能的经过
反过来,利用微分几何的工具,我们还可以反过来定义「指数映射」
- 对任意
- 群乘法 的线性化变成 矢量加法
当然这个关系可以推广到任何两条经过
在微分几何的语言里,给定
,
有一点很重要,就是 「给定这样的切矢量
另外需要注意,
为了简便起见,下面我们只考虑
李代数的李括号运算
李代数的粗定义并不是什么让人十分兴奋的结果,因为此时
幸好,我们可以从李群那里压榨出一个这样的运算。李群是一个群,因此先天具有群乘法这个代数运算。既然我们已经从几何上线性化了李群,那我们不妨也在 代数层面对李群进行线性 化。
此时我们手里有几个关键词:群乘法、单位元和单位元处切矢量,而我们的目标是单位元处的切矢量之间的运算。我们也知道怎么在
- 第一步。
▶︎ 对任何一个给定的
注意,伴随作用有个非常重要的特征:对于任何一条 经过单位元
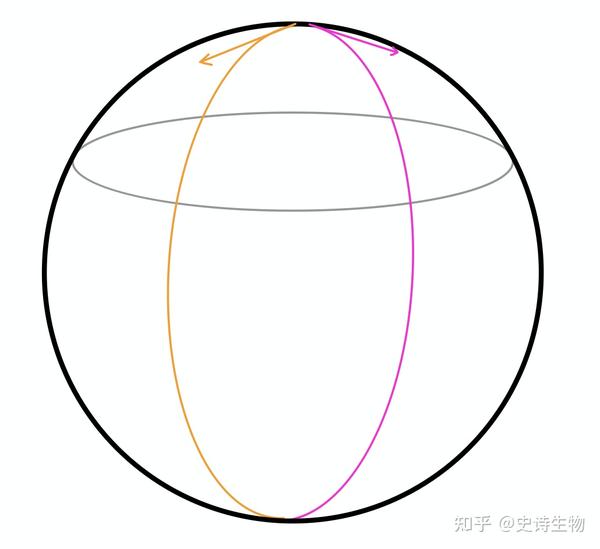 紫色曲线在伴随作用下变成了黄色曲线,相应地其在单位元处的切矢量也随之发生了转动
紫色曲线在伴随作用下变成了黄色曲线,相应地其在单位元处的切矢量也随之发生了转动
2. 第二步。在
▶︎ 定义, 对任意给定
我们不妨标记曲线
于是,
3. 第三步。临门一脚,我们最后令
▶︎ 定义
或者把第二第三步合并一起写
▲ 总的来说,上面的三步走战略相继定义了三个 伴随作用
其中,最后一个就是我们想要的 李括号 。
李括号的性质
上面所定义的李括号实际上就是我们日常生活中用到的李括号,满足 线性性、反对易性、Jacobi-恒等式 。
- 双线性:比较显然,来自求导的性质。
- 反对易性:由于李群的群乘法是光滑的,因此我们不仅可以随心所欲地 求导 ,还可以肆无忌惮地 交换求导顺序 。因此,我们可以考虑
其中我们在第二行和最后一行「用到
- Jacobi 恒等式:先观察到
至此,我们已经在李群的基础上诱导出了其李代数的基本结构。一旦有了这些东西之后,李代数的讨论可以一定程度上与其先祖李群脱离开来了。我们可以最后回顾一下李代数的抽象定义。
♜ 定义: 一个李代数是一个实/复线性空间
下一话 李代数与理想
参考
评论:
renash: 为啥d/dt的逆运算是exp?为啥正好是exp呢?没那么巧过原点的线正好是指数函数吧? (2 赞)
比卡丘流形 -> renash: 是不是属于exp的定义的一部分,我也想知道
史诗生物 -> renash:
可能互逆应该加双引号。Exp 可以从一个李代数元素 X 生成一条 G 中过单位元的曲线 (是一个单参数子群),对其在「单位元处求导」又可以重新获得 X;反过来,在单位元处对一个单参数子群求导可获得其在单位元处切矢量,对其再作 Exp 又可以重获该单参数子群。在这个意义上,可以把它理解为『互逆』。
王云峰 -> renash:
首先对于向量方程 dX/dt=AX,我们知道解可以写成 X(t) = exp(tA) X(0)
对于李群单位元处的一个切向量 A,我们也可以考虑寻找这样的单参数子群 X(t) ,使得 dX/dt =AX,这里 AX 理解为通过群元 X 右乘运算所诱导的从单位元处切空间到 X 处切空间的线性变换,把切向量 A 移动到 X 处切空间(类似微分几何的平移操作);因此形式上也可以把解写成 X(t) = exp(tA)
Kasumizawa Miyu: 为什么说\mathcal{N}年规划而不是N年规划,是在暗示和超对称的关系吗? (3 赞)
史诗生物 -> Kasumizawa Miyu: 嗯可能项目做着做着就超对称化了
Cohomology: 希望以后能看得懂[可怜] (3 赞)
知乎用户Jr0Yid: 期待后文[惊喜] (1 赞)
知乎用户: 推荐一本相应的李代数李群讲义或教材好吗?[拜托]
史诗生物 -> 知乎用户: 我在末尾加了一些参考文献,是几本书和讲义。
Yilu Shao: 家用微分几何[惊喜]
史诗生物 -> Yilu Shao: [机智]直呼内行
轩你的轩: 漂亮
知乎用户: 又是个家用的,追了追了
Housz: 高屋建瓴
吊死的神: 非常感谢您
[马中骐] 物理学中的群论↩︎
[Di Francesco, et.al.] Conformal Field Theory, chapter 13↩︎
[Ebrahim] Semisimple Lie Algebras and the Root Space Decomposition↩︎
[Nakahara] Geometry Topology and Physics↩︎
无穷阶可导。↩︎
所以群表示是非常有用的,因为它至少解决了这第二个困难,把非线性的运算简化为对线性空间的线性映射↩︎
比如割圆术、微积分↩︎
点和点之间不能作任何运算;如果引入微分流形上函数,则可以构成另一种线性结构↩︎
并且保持所有的信息。↩︎