为什么自然数的和等于 -1/12？ - 返朴 的回答

欧拉是如何证明出来的？

数学, 莱昂哈德·欧拉（Leonhard Euler）, 数学分析, 分析学, 级数

前段时间收到一位热心读者的邮件。信中提到，如果认定1-1+1-1……=1/2为事实，就会得出1+2+3+……=-1/12这样难以令人理解的结论。这位读者所提及的自然数求和问题，恰巧在量子理论和弦理论中都起到颇为重要的作用。从真空的能量，到时空的维度数量，都与自然数之和有着微妙的联系。在这个小小的数学魔术里面，甚至还隐含着时空不连续的秘密。

撰文 | 董唯元

数学老师曾告诉我们，只有收敛的级数才能求解无穷项之和，然而在一些科普书中，却会遇到一个神奇的求和：

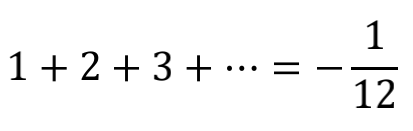
所有自然数之和怎么会是负数，而且还是个分数？这到底是人性的扭曲，还是道德的沦丧？

把对称轴当作级数和

想要理解这个古怪的结论，我们先来看一个简单的例子：1, -1, 1, -1, ……这个序列可以求无穷项之和吗？意大利数学家格兰迪（Dom Guido Grandi，1671-1742）早在1703年就开始认真琢磨这个问题，可以说，这是所有发散级数求和研究的起点，这个序列后来就被命名为“格兰迪级数”。

意大利数学家格兰迪丨图源：维基百科

也许有小伙伴猜测，这个序列中1和-1的数量既然同样多，那么总和就应该等于0。可惜这样的猜测是错误的。无穷集就像个再生能力很强的变形虫，部分与整体同样多。我们从序列中拿走任意个1或者-1之后，剩下的1和-1数量仍然相同。如果所剩下的1和-1加和为零的话，那么岂不是总的求和仅由先取出的1或-1的数量决定——也就是任意整数。这显然太不靠谱了，看来压根不能依靠比较1和-1的数量来求和。

还有个办法，就是借助收敛的级数寻找线索。我们知道，在|q|<1时，

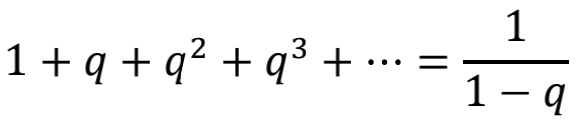
现在我们粗暴地让q=-1，于是就出现了

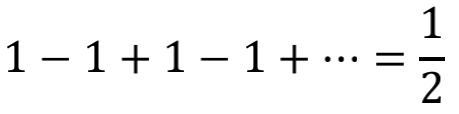
这个结果似乎还能令人接受，可是，q=-1毕竟是个“不合法”的条件，我们需要更合理的途径来安抚内心的不安。如果把这个级数的前n项和记做A(n)，我们现在动手来求 A(∞)。

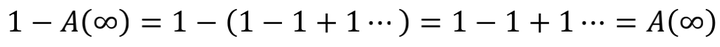
哈！根据这个等式，我们又一次得到了 A(∞)=½ 的结果。这回貌似没有明显违法的地方了，警察来了也不怕。可是，总还是感觉哪里不对。

A(1)=1
A(2)=1-1=0
A(3)=1-1+1=1
…

可以看出A(n)在1和0之间来回跳动，按照极限的定义，

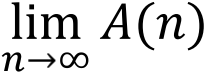
这个极限不存在。当我们写下 A(∞)这个符号时，它究竟指代什么，还没有清楚的定义。其实这也是发散级数求和的基础问题：如何定义发散级数的和。

相关的定义不止一种。大体来说，主要有切萨罗求和与阿贝尔求和两类，另外拉马努金和黎曼等人也发展出许多更一般性的理论，中间还掺有源自欧拉的诸多贡献。那些数学语言虽严格，但催眠和劝退的副作用也不小，所以本文不打算纠结于那些从集合论谈起的基础定义，只使用非常“物理”的视角来定义： A(∞)表示所有A(n)的平均值。

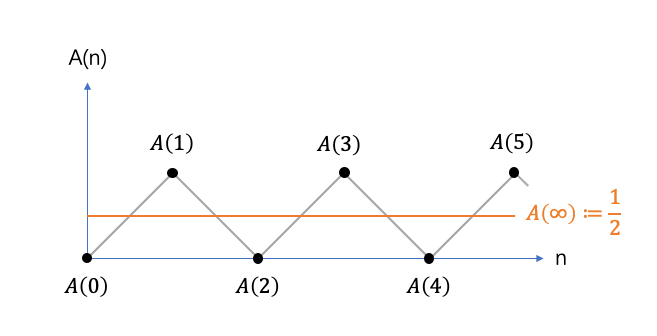
以“平均值”定义的求和方式，使许多发散级数都可以进行求和。例如

1-2+3-4…

这个级数，也可以用同样的方法直接用眼睛瞪出结果。我们用B(n)表示前n项和，即

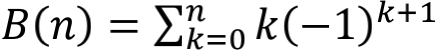
，那么

B(0)=0
B(1)=1
B(2)=1-2=-1
B(3)=1-2+3=2
…

把这些B(n)所对应的点画在图上之后，完全不需要动笔计算，用眼睛就可以直接看出所有B(n)的平均值是1/4。

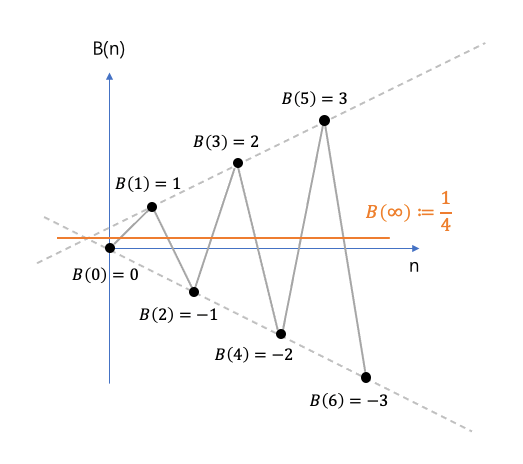
如果只看图还不放心，我们也可以借助前面 A(∞)=½ 的结论来推算 B(∞)：

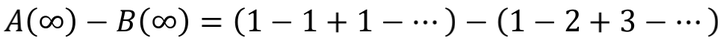
稍微调整等式右边的计算顺序，先让前面括号内第n项减去后面括号内第n项，然后再做加和。

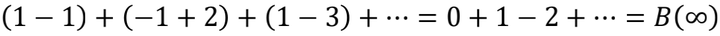
即 A(∞) - B(∞)= B(∞)

所以 B(∞)=½ A(∞)=¼

把自然数之和变成-1/12的魔术

当然，画出点来再用眼睛直接瞪出结果的方法，有时候也需要一些技巧。就以全体自然数之和为例，我们同样地令C(n)代表前n项和

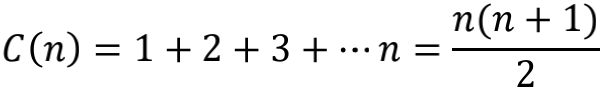
麻烦出现了！显然C(n)对应的点都分布在一根上扬的抛物线上，没办法直接看出平均值，而且看起来压根就不存在有限的平均值！别急，我们可以继续变形。

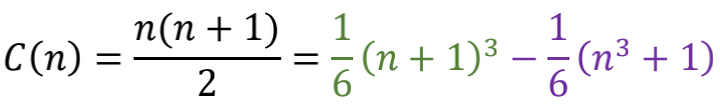
这样我们就把每个C(n)对应的点，都拆成上式中绿色项和紫色项所对应的两个“半点”分别画出来，居然又可以凑成两条对称的曲线。

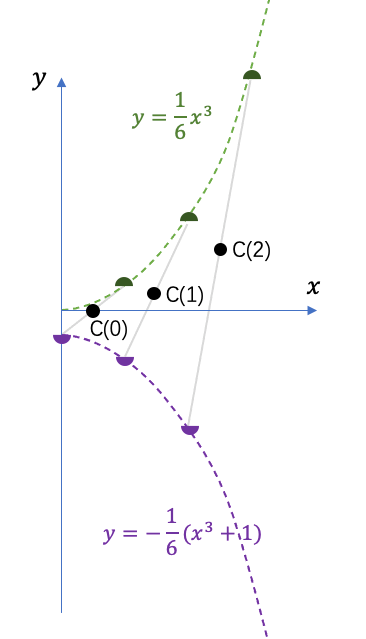
当我们把无限个“半点”都辛苦画完之后。就可以指着两根曲线中间的对称轴宣布：

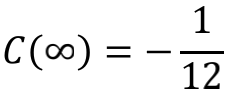
因为所有C(n)的平均值就等于所有“半点”的平均值，而两根曲线上的“半点”分布完全对称，只在绿色曲线的开头位置差了一个无关紧要的0。

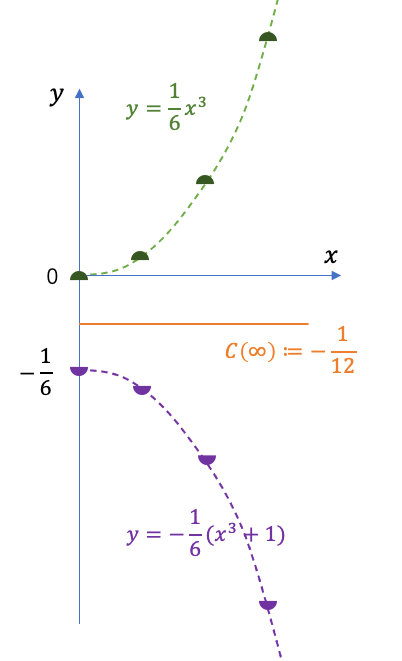
除了看图猜值，我们也可以借助刚才的 B(∞)=¼ 那个结果，再来计算一遍 C(∞)。

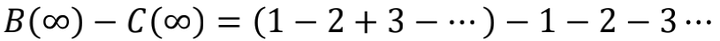
调整顺序后

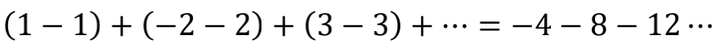
于是得到

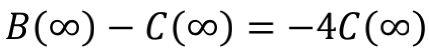
所以

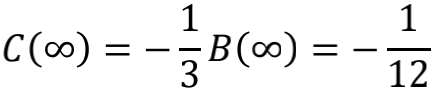
其实，能够得到 -1/12 这个结果的途径还有许多。例如神奇的Zeta函数

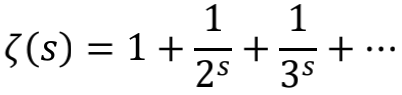
这个以复数s为变量的函数，因著名的黎曼猜想及其与数论的紧密联系而被反复研究。数学家们可以写出这个函数的许多种变化形式，其中一种解析延拓到全部复平面的形式是

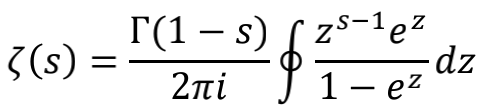
用这个形式也可以计算出

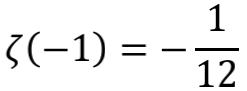
既然经过这么多五花八门的方式，都殊途同归到 -1/12 这个结果，我们是不是可以把 1+2+3+…=-1/12 这个式子堂而皇之地写进中学课本中呢？相信许多人会跟我一样，对此仍惶恐不安。因为在前述所有推演过程中，都埋藏着一个颇为隐蔽的问题，那就是等号的意义。将

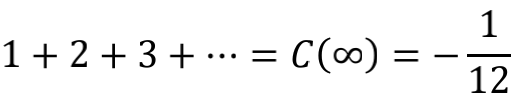
或

直接写成

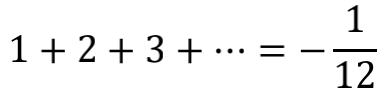
似乎理所当然，但其实两个式子中，前面的“=”代表的是“定义为”，而不是量值相等。所以，更清楚的写法应该是

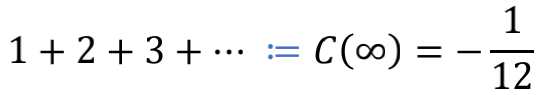
和

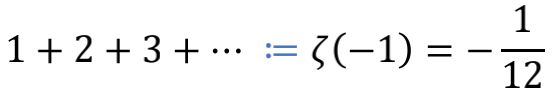
这样就能看出， -1/12 这个数值，并不像1+1=2那样自然天成理所应当，而是需要事先假定“全体自然数之和是一个确定的数”，然后再精心挑选出一个逻辑自洽性最好的数值，指定其为全体自然数之和 。只不过当逻辑自洽性和直觉发生明显冲突的时候，我们都会感觉惊诧，这在数学发展的道路上已经不是什么新鲜事了。

伸向无穷大的剪刀

前面的讨论中，我们直接无视了数学极限概念，粗暴地使用平均值当做发散级数的和。现在让我们重新捡起极限概念，从另一个角度看看-1/12是怎么跑出来的。

对 C(n) 这个发散级数，我们可以引入某个剪刀函数 f(x) 来压制那些趋向无穷大的项，从而使发散的趋势在某个特定的位置N附近停下来，并最终收敛到某个极限S(N)。这样我们就用标准的极限概念构造出一个S(N)，当N有限时，S(N)是个有限值，而当N趋于无穷大时，S(N)就对应着全体自然数之和。

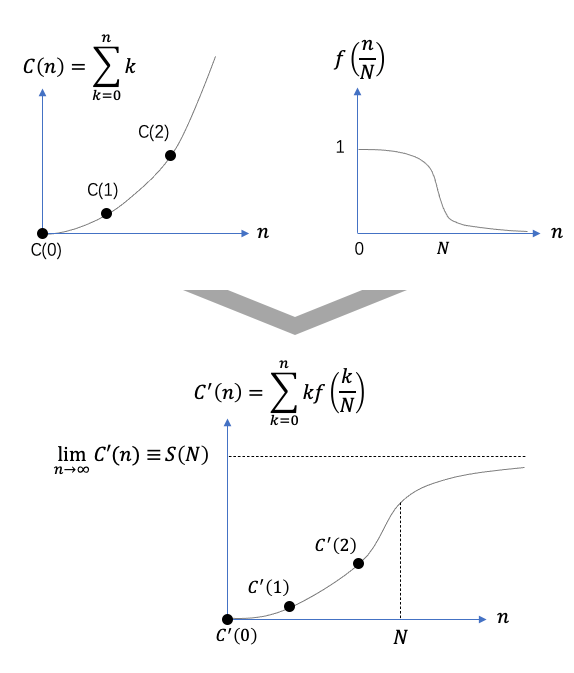
通过数值计算，我们发现S(N)随着N的增加而奔向正无穷。这倒是符合我们先前的直觉了，可是说好的-1/12呢？别急，我们再把S(N)用1/N展开看看。我们发现S(N)在大N的数值结果，可以被下面的展开式很好的拟合

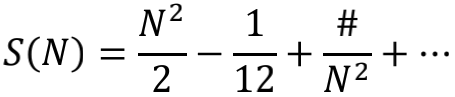
哈！居然又看到了这个-1/12，它是S(N)展开式中的常数项。也就是说，在S(N)中与N的变化无关的成分，就是-1/12。当N足够大时，那些含1/N的项都可以忽略，S(N)可以被看做一根最低点在-1/12处的抛物线。

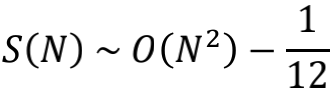
我们再取剪刀函数 f (x)=e-x 试试。此时

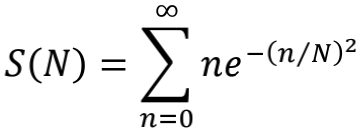
这个求和可以严格计算出来。我们先对下面的等式两边求β的导数

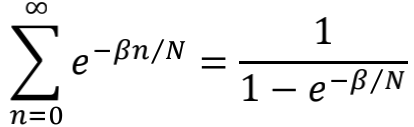
可以得到

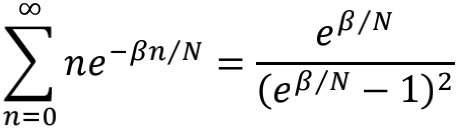
同样在大N条件下做1/N展开，就得到

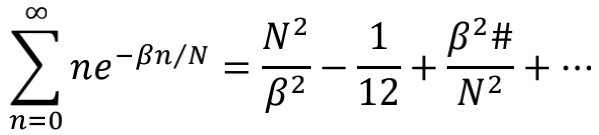
取β=1就得到

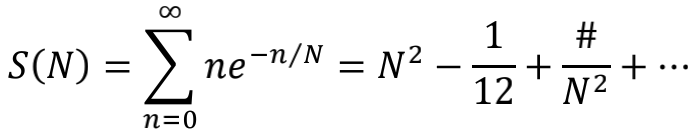
同样也出现了常数项-1/12，而且也是根下垂到-1/12处的抛物线

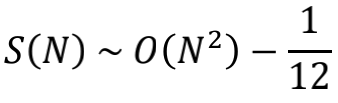
如果 f (x) 直接取为跳变函数，也就是在 n= N 处突然截断，那么

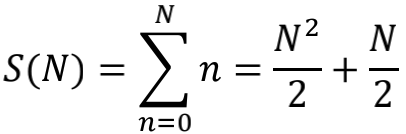
就不会有-1/12这个常数项。

看起来，除了跳变函数的突然截断，其他平滑的截断方式都能得到

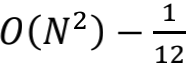
这个有趣的结果。这似乎是告诉我们，全体自然数之和即使注定无法摆脱走向无穷大的宿命，却出于某种神秘的理由一直对-1/12情有独衷。亦或可以说，

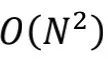
发散项只是平庸无奇的底色，而-1/12才是刻写在底色上的性格内核。

真空的能量

站在实用的视角来说，我们有时候需要像使用收敛级数一样处理自然数之和，所以就不得不找到某个确定的“缰绳”来驾驭。比如在研究真空能量的时候，物理学家就遇到了全体自然数之和，而且非常希望这个和是个确定的数。

在量子场论的理论模型中，真空就像一张立体弹簧网，由无数小弹簧横纵交织而成。而所谓粒子，就是其中某些小弹簧的振动足够剧烈，以至于远远望去以为弹簧网中出现了什么异物似的，但只要凑到近处就会看出，那里除了振动本身别无他物。也就是说，粒子本质上就是真空的振动。因此，当能量变化时，粒子的数量不必受任何守恒律的约束，可以凭空增加或者减少。不过，粒子能否产生或消失却与小弹簧的振动频率有关。在振动频率为ω时，粒子数n与场的能量E之间存在这样的关系：

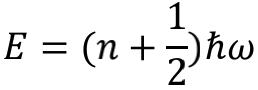
从关系式可以看出，真空每攒够一份ћω大小的能量，就会产生出一个粒子；反之每减少一份就会擦除一个粒子。或者干脆说，每个粒子其实就是个ћω大小的能量包。有趣的是n=0时，它对应着真空里没有粒子的情况，此时能量是½ћω。也就是说，当真空的能量低到不能再低的时候，能量仍然不是0，这就是 真空零点能 。下面我们来具体计算一个有限空间内的真空能量，看看它与全体自然数求和到底是什么关系。

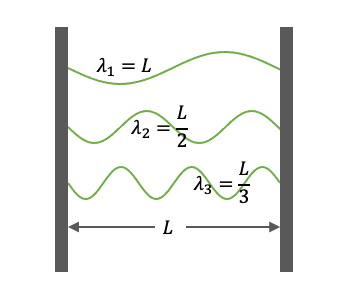
我们知道，两端固定的弹簧上只能存在驻波，即波长的整数倍恰好等于两端距离的波，因为只有这种波在来回反射过程中可以维持能量，其他形式的波都会自我消减。导体对于电磁场也有一模一样的作用。在距离为L的两块金属板之间，只能存在波长恰好为 λn= L /n 的电磁波，其中n是正整数。每个这样的电磁波频率为

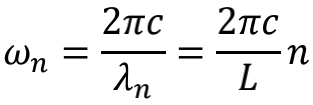
将所有频率的零点能累加起来，真空中总能量就是

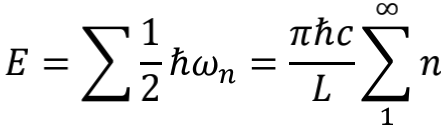
瞧，自然数之和

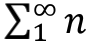
就这样出现了，现在你应该能够理解，物理学家们是多么希望

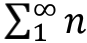
是个确定数值了吧。更有意思的是，如果姑且憨憨地认为自然数之和就是-1/12的话，我们甚至可以设计一个物理实验来验证这个结论。

如下图这样放置三块相互平行的金属板，使甲乙之间距离为a，乙丙之间距离为b。

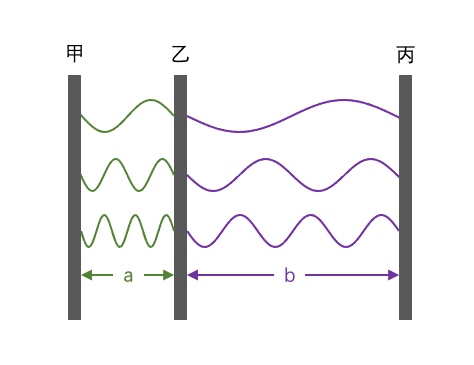
根据刚才的结论，我们知道甲乙之间的真空能量是

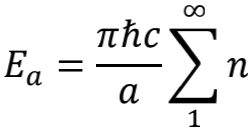
乙丙之间的真空能量是

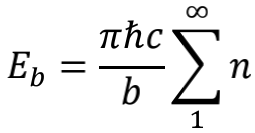
现在我们想知道，当a＜b时，中间位置的金属板乙会受到哪个方向的力。根据能量对位置的偏导可以求解受力情况。结果发现：如果

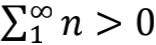
的话，金属板乙会受到一个向右的力；反之则受到向左的力。

其实，实验装置还可以进一步简化，我们可以把最右边的丙拿到无穷远处，只留下甲和乙，然后测量甲乙之间是吸引还是排斥，如果相互排斥，就说明

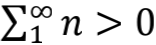
，反之则说明

。

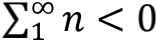
这个实验设想最早由荷兰物理学家卡西米尔（Hendrik Casimir，1909-2000）在1948年提出，当然提出实验的目的才不是测量自然数之和，而是为了验证真空零点能的存在。事实上，卡西米尔当年在提出这个实验的时候，就已经预言两金属板之间相互吸引，也就是对应

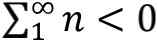
的情况，因为他的理论推算过程已然采用了解析延拓后的黎曼Zeta函数。1996年，华盛顿大学的Lamoreaux用实验证实了卡西米尔效应的存在，论文发表在1997年1月的《物理评论快报》（ PRL ）上。

需要澄清的是，卡西米尔效应的实验证实，只能说明真空零点能的存在，但是并不能真的用来验证数学意义上的所有自然数之和。其实，现实中的金属板只能阻拦有限频率范围内的电磁波，当频率大过某个数值时，金属板就无法阻拦这种极高频率的波。所以从更精确的角度计算卡西米尔效应时，需要考虑这种高频截断。不过具体计算会用到欧拉-麦克劳林公式和伯努利数这些催眠的内容，本文就不再涉及了。

下面我们转到弦理论，看看所有自然数之和是如何与维度的数量产生关系的。

时空的纬度

前面提到，两端固定的一根弹簧之上只能存在驻波，所有振动频率只能是最低频率的整数倍。对一根两端完全自由的弦来说，结论同样成立。两端固定意味着端点速度为零，而两端自由则意味着端点的加速度为零。二者之间的差别，无非就是傅里叶分解时该写成

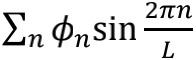
还是

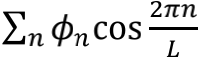
而已。也就是说，长度为L的弦，肯定有个像自然数序列一样的离散频率谱

。

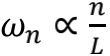
另外，弦理论中的量子化方式与量子场论所使用的技术手段如出一辙，所以同样存在

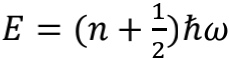
关系。这意味着能量最低的弦并不是完全静止，而是具有

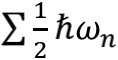
的能量，而且在每一个可以振动的维度上，都有这些能量。

注意，仅具有最低能量的弦不会被当做粒子看待，只能被视为真空。表现为一个光子的弦，至少需要高出基态能量一份大小ћω1的能量。这份能量在一个空间维度上以光速传播，就是一个光子。根据相对论，在这个光子传播的维度上，不再具有振动的自由度，而剩下的空间维度里，弦都还具有基态能量。

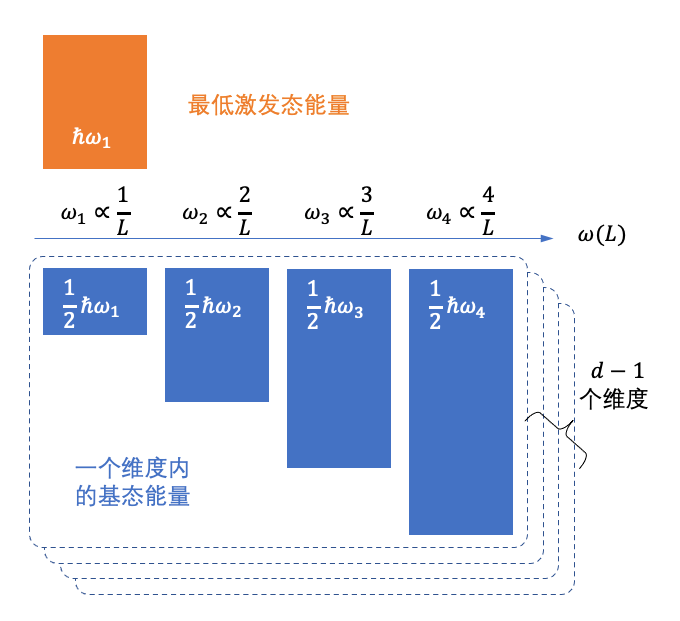
假设空间维度数是d，那么一个被激发成光子的弦所具有的最低总能量就是

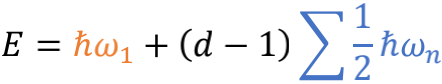
注意到 ωn=nω1 ，这个光子的总能量就变成了

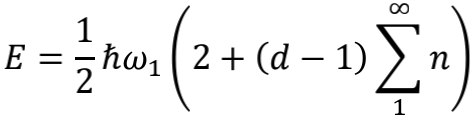
妥妥的又出现了

。

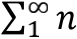
相对论告诉我们，光子的最低能量应该是零，所以跟相对论兼容的弦理论必须满足

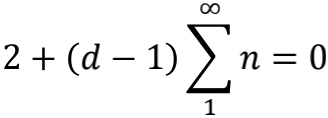
推演到这里，我们就要祭出

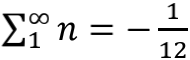
这个大招，求解出d=25，也就是空间维数必须是25维，加上时间，总共26维时空。

在超弦理论中，由于超对称因素的引入，弦的基态能量提升为3倍，光子能量约束条件变成了

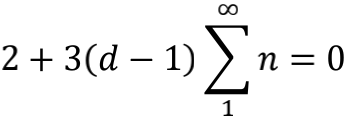
由此求出d=9，加上一个时间维度，总共凑成10维的时空。

以上就是玻色弦理论要求25+1维时空，以及超弦理论要求9+1维时空的故事梗概，希望读者能借助这些实例，对自然数之和在物理中的作用建立一些具像理解。

离散的时空

为了保持话题的收敛性，前文论述中刻意略过了许多有趣的细节。例如在弦的基态振动模式中，如果存在

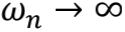
的成分，那么必然有

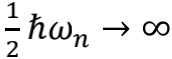
，这就意味着仅在弦的一个振动模式里，就包含了无穷大的能量。同样的，真空零点能的计算中，也会不可避免地含有能量无穷大的成分。这显然都太不合适，我们的理论模型需要有个边界，来防止这种在极高频率方向“紫外灾难”的发生。

之所以能产生无限大的频率，就是因为我们允许存在无限小的波长。那么自然就会意识到，可以消除“紫外灾难”的理论模型中，空间必然存在有限的最小尺度。更直白地说，就是空间不可能是连续的舞台，而必须是离散的梅花桩。这个最小尺度究竟是多少呢？一个天然的候选者，当然就是普朗克长度。

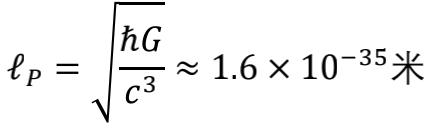
如果某个粒子的波长比普朗克长度还要短，那么这个粒子就会由于具备了太高的能量而把自己就地变成黑洞，而且这个黑洞所覆盖的区域又会超出普朗克长度。于是，普朗克长度就成了现有理论中最为自然的时空基本像素。

于是，先前的

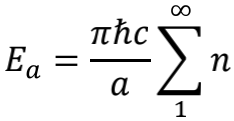
就变成了

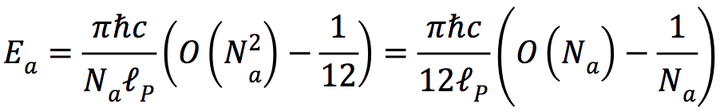
我们发现，甲乙板间的能量 E a 分为两部分，其中一部分与 N a 呈正比，另一部分则呈反比。乙丙板间的能量 E b 也是同样情况。

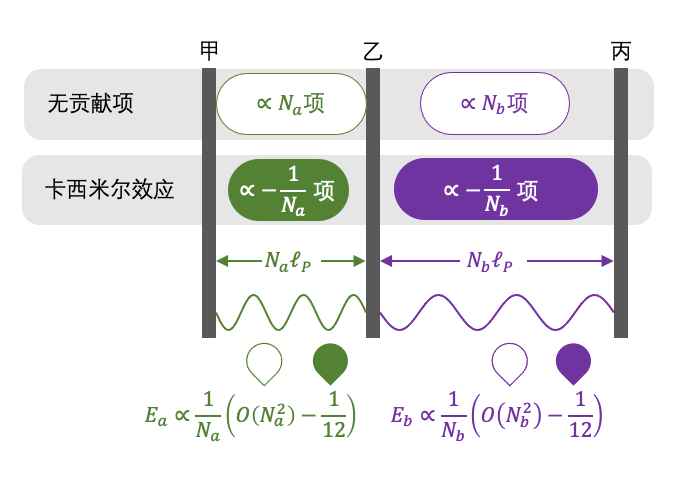
显然，呈正比的那部分能量，在乙板左右产生的作用力始终相互抵消，只有第二部分呈反比的能量，才对乙板产生了作用力。由此可见，卡西米尔效应是在两个巨大的首项恰好相互抵消之后，在第二项上显现出的效应，所以这种力异常微弱，只有把两个面积达平方米量级的金属板靠近到微米距离时，才能产生可供测量的吸引力。

现在我们才算真正解释了卡西米尔效应与自然数之和的关系，如果未来再遇到有民科企图用这个实验来证明自然数之和是个负数，尽可以毫不犹豫地送他一个白眼。

RHCPeppers: 牺牲一点严谨性，带来更直观的感受，是一篇好的科普文！ (136 赞)

起风了 -> RHCPeppers: 哪里不严谨？ (3 赞)

今天有喝可乐么 -> 起风了: 文章最开始就说了呀，并且这个只是个物理意义，不是数学意义 (12 赞)

夜林 -> 起风了: 计算A,B那里随意加减括号，无穷级数是不能随意换序+括号的

kknd:

又研究了一段时间，终于理清了来龙去脉。
所谓自然数之和等于-1/12本身就是欧拉时代搞出来的，那时候极限的概念还没有搞清楚。

后来，柯西定义了∞的概念，并严格给出限制：求无穷级数需要证明他的收敛性，在没有证明他的收敛性的前提下，任何结论都是错误的。并否定了欧拉的所谓自然数之和，自然数平方和一类的猜想。

后来，印度数学家拉马努金在去英国学习正统数学前，凭借非凡大脑算力，把古人很多想法的公式都整了一遍，其中错错对对都有，包括欧拉搞过的自然数之和，并命名为拉马努金和（这兄弟只写公式从不证明，所以错错对对都有）。

再加上解析延展的定义，本身就是更改了定义或者规则。

因此可以肯定在当前∞的定义下，所谓自然数之和等于-1/12，是错误的！

注意，这个先决条件就是柯西定义的∞条件下！ (100 赞)

Sven -> kknd: 系啊系啊 (1 赞)

山林:

真是太奇怪了，全是正数，加起来最终是负数。
确实是和直觉不一样。
我不适合数学。 (54 赞)

TAimeur -> 山林: 其实答主中间也说，严格来说并不叫“量值等于”，而叫“定义为”。 (159 赞)

抓狂 -> 山林:

是啊，反直觉啊

一直攒钱会攒没了[好奇] (67 赞)

大果粒酸奶 -> 抓狂: 是一直攒钱攒钱，最后攒到欠钱？！！ (16 赞)

柯西 -> 山林: 其实这里的等于已经不是你理解的那个等于了，而是一个函数解析延拓之后的结果，说白了就是人为的规定了全体自然数的和是-1/12，而且答主把这么规定的原因讲的非常清晰透彻 (40 赞)

takeshi taki -> 抓狂: 因为你那都不是无穷，你无论攒多少都是一固定的有限数，不能用实际物品概念去理解无穷。 (10 赞)

takeshi taki -> 山林: 这是因为涉及到了极限和无穷，涉及无穷的问题很多都反直觉，我觉得是因为我们的生活体验里面并没有真正的无穷，无穷只是思想层面设计出来的东西，只要在特定领域内做到逻辑自洽就好。 (21 赞)

kknd -> 山林:

你是对的，楼主才是错的，他用了太多直觉，比如绝对值小于一的条件算法，他居然敢把-1带进去，这就是扯淡。

数学不是感觉，更不是粗粗，而是理论和条件的精确匹配。 (4 赞)

ThunderRainbow -> 山林: 加起来不等于啊，全体正整数的和等于正无穷，注意是等于正无穷，至于负十二分之一是取了个"平均值"，就像1+1-1+1-1+1-1.......这个级数是不收敛的，既不等于0也不等于1也不等于-1，取个平均才是0，所以正整数的和等于正无穷，平均于-1/12，这样明白了吧[笑哭] (5 赞)

红薯: 见过的最好的一篇介绍-1/12的文章[捂脸] (83 赞)

吴忱: 你说的这个读者，他是不是叫欧拉，他是不是还失明了 (46 赞)

巡游人:

C(n)那个看懂啦！于是就这个部分来探讨一下。

“因为所有C(n)的平均值就等于所有“半点”的平均值，而两根曲线上的“半点”分布完全对称，只在绿色曲线的开头位置差了一个无关紧要的0。”

我发现这里有一个漏洞呢——我们把所有的自然数一分为二画出来上下两半“完全对称”的曲线，但关键在于，实际上我们并不仅是在开头多出一个无关紧要的0，更意味着在末尾处有一个“末尾数的上半拉”被向后挤了一个位置。但因为曲线是无限的，我们自然认为其末尾在无穷远，分不清到底最后一个是谁，就马虎过去了。

我记得我中学时老师讲起极限的概念，曾经说过一句让我恍然大悟的话。说两个人比大，甲说1乙说2、甲说200乙说201，那永远说不完；但如果乙说“我比你大1”，那好了，无论甲说几乙都比他大。

回到这个C(n)里，当你在开头加了一个0，把上半个曲线延
X轴向后推了一格，但你算平均值时可是要上下对齐来算的呀，被挤的那个半拉数就被抛掉了，这就是总和变成-1/12的真正原因——无论你这个曲线画到多远，都有一个上半拉数被你抛掉了。 (28 赞)

kknd -> 巡游人:

他抛掉的那个就是产生所谓
‘结果“的原因，哈哈哈
你是对的。

天坛 -> 巡游人: 如果推回去，所有自然数的和就为0了

巡游人 -> 天坛: 并不是。抛掉一个上半拉数，总体平均是-1/12，但并不能说加上这个上半拉数总和就是0了。事实上我们说“所有自然数”的时候这个上半拉数是远大于前面这些-1/12的，这刚好符合我们“所有自然数之和是无穷大”的感觉。 (2 赞)

Freedom -> 巡游人: “定义为”负十二分之一 这件事 根据答主后面的论证 应该是正确的 但我觉得你说的 很有道理 蹲一下 有 dalao 解释恳请t我一下谢谢啦

天坛 -> 巡游人: 是我理解错了

高堡名人 -> Freedom: 没法“定义为”负十二分之一，否则一定会导致∞=-1/12，为了使这套理论自洽又得不停地定义别的东西，代价太大，收益几乎没有。其实你看文章最后一句就明白了“如果未来再遇到有民科企图用这个实验来证明自然数之和是个负数，尽可以毫不犹豫地送他一个白眼。”，说白了作者并不需要令自然数之和等于-1/12 (2 赞)

巡游人 -> 威化饼干:

对称还是不对称，这是两个语境之下的叙述，而明白了这两种描述之间的差异是从何而来，就是理解-1/12这个反常识的结果的关键。
所有思想实验都一样，如果导致了反常识的结果，那一定是其中某个环节没想明白。而如果不把这个关键环节揭示出来，只是醉心于结果的惊世骇俗，那就流于噱头了，失去了思想实验该有的价值。 (1 赞)

威化饼干 -> 巡游人:

是的，对称和不对称是两个语境下的叙述，说上下对称，是指每下一个自然数的下半点和当前自然数的上半点一一对应，这样每次增加下一个自然数，都会先只先增加它的下半点，也就是所谓有一个上半点在计算时被挤掉了，这也确实是得出的平均值结果是负数的原因，这一点我认同你的观点。
说上下不对称，是指这里的操作并不是让同一个自然数的上半点和下半点一一对应，因此才会在前面多出一个零。
而我想说的是，这里面漏掉最后一个上半点的操作，在计算有限集时当然是错的，但当放在计算无穷集里面，它就并不是马虎过去的，而是严格成立的。正是因为有了上面的一一对应关系，才说明了上下两个无穷集元素数量相等，既然上下半点数量相等，当然能够上下一一抵消来计算平均值，于是在计算平均值时看似漏掉最后一个上半点的操作才能成立，因为在无穷集里面不存在最后一个上半点的说法。
换一个角度，你也可以认为在无穷集里面，数学家们统一定义了这个所谓的马虎就是成立的，这也是集合论的基本思想。 (2 赞)

kknd:

扯淡，高等数学中绝对不能不看条件。
人家都说了绝对值小于一有效，作者居然“粗暴”的认为绝对值等于1也有效，得出的结果肯定是错的。

这就是考不上大学的人才会犯的错误，更蠢的是居然还有人鼓掌支持？ (17 赞)

黑暗西斯尊主 -> kknd: 那是级数的定义不同导致的，这里可以认为是zeta（-1）或者级数的拉马努金和 (7 赞)

憬宝 -> kknd: ？？你的论文发一下吧 (23 赞)

黑暗西斯尊主 -> kknd: 首先，文中举的例子都是符合文中级数算法的，和常规高数判断级数收脸那一套体系不一样，没有乱用，另外你没事嚷嚷牛顿定律和相对论干啥，牛顿定律只是相对论低速下近似而已，文章不能仔细看看吗？ (24 赞)

红薯 -> kknd: 解析延拓了解一下[捂脸] (8 赞)

杜乌龟 -> kknd: 晕 你真是笑死人了 (3 赞)

Dest1n1 -> kknd: ？答主难道没有说带入-1是不严谨的证法吗？我记得他后面给出了发散级数的定义吧 (11 赞)

qwert -> kknd: “”这个结果似乎还能令人接受，可是，q=-1毕竟是个“不合法”的条件，我们需要更合理的途径来安抚内心的不安。”你是看到这一句就没往下看吧 (9 赞)

冰凝之心 -> qwert: 他大概只能看懂到这里，然后就来评论区了 (5 赞)

炉石真鸡霸本霸: 我觉得这不是科普，这是在嘲笑我是个文盲[捂脸] (36 赞)

知乎用户: 每当知乎上出现这种专业性极强的问题，人们总是喜欢挑一个看起来最厉害的回答点赞。剩下的回答都没人看，不管他们答得怎么样。 (27 赞)

脆皮鹦鹉: 说真的，为啥我学不会高等数学，因为他有些定理乍一看总是不合常理[语塞]。还是老老实实从事可以用经验解决问题的工科研究吧[语塞]，数学什么，科学家说这是定理拿来用就行了[语塞]。 (9 赞)

银翁 -> 脆皮鹦鹉: 西方数学从此走向歧途。“指驴为马”式地乱下结论，成为“弥天大谎”唬人的经典。人们应将“晦涩”的数学变成“明白”的数学；不然就会让数学演变退化为“自欺欺人的学科”。数学大厦不应让“蚁穴”“蛀虫”去损毁！错误的“歪理”岂能迷信成为“定理”，又如何可“拿来用就行了”？ (1 赞)

脆皮鹦鹉 -> 银翁: 本身数学就是工具，学习数学是为了理解特定的思维方式。本身数学就是抽象学科，很多人不理解是因为无法将抽象的东西具象化。历史上的数学家们为了解决这个问题已经做出了很多贡献，为了理解平面几何关系引用了平面直角坐标系，同理又引入了空间直角坐标系。但是在这个基础上发展的微积分。以及在欧氏几何基础上发展的拓扑分形几何等已经不是普通人可以轻松理解的了。或许您对数学教育有更深刻的研究，但是我只是一介普通人罢了，无法理解的那么深刻。说到理学和工学的关系，常理上就是理学在小范围研究，而工学是推广到更广的层面。工学大部分只是基于理学的研究基础去改良工艺并推广社会。为什么不能拿来用呢？理工学习研究本身就是从抽象想法到具体实现的一个过程。工学在研发端下游，理学在上游罢了。 (4 赞)

银翁 -> 脆皮鹦鹉:

如果认定1-1+1-1……=1/2为事实，进而认为1-1+2-2+3-3+……=-1/12 。
就得出自然数1+2+3+……=-1/12的结论”。这样结论不仅难以令人理解，而且是错误的结论。

这种数列关系可以成立，用到波浪曲线的调频调幅的计算倒可借用；但结论是错误的。怎么能将这样的正负摆动数列叫作自然数列？怎么归结是自然数之和呢？！什么是自然数？什么是自然数列？什么是自然数之和？那个题主已将不是自然数列，错误地认定为自然数列，偷换了概念！自然数之和是指加法运算，可求和之数列却出现负号或减号，这还能算自然数加法求和吗？！如说是负号，是加上一个负数，那么负数还能算是自然数吗？这是基本概念的混淆！如说是减号，那还能算是加法求和吗？这已成为加减法混合运算，求得的和差平均值！总之，这种变异的特列数列的和差平均值等于-1/12？但也不能说是自然数的和等于-1/12！这结论是错误。不知是翻译出差，还是有人故意忽悠，制造数学混乱？或反映有些人对自然数与自然数列缺乏清晰的认识，缺乏明确的概念。 (8 赞)

脆皮鹦鹉 -> 银翁: 啊这 我并不是回答问题的人

太平咸阳 -> 脆皮鹦鹉: 而且自然数的求和应当是大于1+1+1+...的级数的，1+1+1+...是无穷

傻猫 -> 银翁: 这就是数学的趣味了，你所发现的‘明明是错的’结论却能从无法理解的角度发挥用处，最后人们在从结论入手尽力理解它就发展出这门学科了 (1 赞)

我真的不会代数 -> 银翁: 什么叫”明明是错的“？”明明“可不是一个良定义的词汇。在一般意义下确实是错，但框架不一样它就可以是对的。

银翁 -> 我真的不会代数: “指驴为马”式地乱下结论，是什么“框架”？是什么“它就可以是对的”？！

from: https://api.zhihu.com/appview/api/v4/answers/1749521577