群论 (Group Theory) 终极速成 / 群表示理论
title: 群论 (Group Theory) 终极速成 / 群表示理论
url: https://zhuanlan.zhihu.com/p/314567658
author: 東雲正樹 (addf05a0e14de70d36baf1223c0a01e6)
column: 物理中涉及的数据处理方法 (c_212428490)
voteup: 845 赞同
created: 2020-11-22 07:06:40
updated: 2021-08-15 12:00:00
fetched: 2021-09-30 19:06:40
count: 约 29603 字
version:
tags: [理论物理, 群论, 线性代数]
from 专栏 物理中涉及的数据处理方法
话题:
理论物理, 群论, 线性代数
正文:
序言
前面三章都是 [群论 ABC], 目标就是搞清楚研究对象是啥, 以及了解一下业内的一些黑话. 第四章就是在前三章的基础上引入群表示的概念, 我们的重点是
目测第五章结束之后就可以直接开始研究李群了, 相信这是大多数人看本文的目的, 这才终于派上用场了是吧? 其实学习一点儿代数概念即使没直接用上也能很大的提高几何观点, 这样看待物理结构就可以有更高更清晰的视角了. 所以前五章也是很神奇有趣的东西, 很值得了解一下, 尤其是看我写的这种降级阉割版本, 可以说完全不可能出现过度学习的情况.
目録
4. 群表示理论
4.1. 群表示
4.2. 忠实 幺正 正则
4.3. 群代数
4.4. 类函数
4.5. 等价表示
4.6. 不可约表示
4.7. Schur 引理一
4.8. Schur 引理一的推论
4.9. Schur 引理二
4.10. 群中心, ker R 与忠实性
[附录 C] 线性空间, 线性变换与内积
[附录 D] 有限高维空间往低维空间线性映射
[附录 E] 复空间线性变换至少有一个非零本征矢
4. 群表示理论
表示结构是个 3P 结构.
3 名 Player 分别是 [群
] [表示空间 上的一般线性群 ] 与 [同态映射 ].
前面我们从群的定义出发, 很抽象地介绍了群的基本概念与性质, 要想深入的研究群的结构就必须要用数字精准地将群刻画出来, 而我们将要选择的数学工具就是线性空间与线性变换.
具体的做法是定义一个从所研究的群到线性变换群的一个同态映射,
┣ 然后通过研究线性变换的性质来间接揭示群的结构.
┣ 再说的通俗一点就是把群元素都用矩阵对应出来, 然后用线性代数里那一套去玩群.
┗ 如果你把所有可能的表示结构都研究完了, 那么这个群应该就可以说是被你研究透了.
所以你必须先知道什么是线性空间, 这是量子力学的任务, 这里顶多给个极其简略的 [附录C].
4.1. 群表示:
设
✦ 复一般线性群有以下两个等价的定义:
(1).
(2).
要求可逆主要是因为要构成群, 所谓可逆在矩阵意义上就是要求矩阵的行列式不为零.
此集合显然构成群, 群单位元就是恒等映射[2], 也可说是 阶单位阵.
此后我们对此将不作严格区分, 即里的既是线性变换又是矩阵.
这个概念肯定也是存在的, 就是 维实线性空间上的一般线性群.
✦ 群
即
或 .
┗ 对
此外, 群表示也有非线性表示, 但我们从头到尾都不会涉及非线性表示.
┗的数域其实也不一定要 , 但 是最简单的且完全够用了, 所以我们就只研究它[3].
值得一提的是,是无限群, 所以一定可以改写为是有限群 跟他的一个子群同态.
┣ 这个子群我们称之为线性变换群, 少了一般俩字就成了子群.
┗ 线性变换群可以写成同态映射的像构成的群, 即, 当然这是个废话.
其中
说明一下符号
:
┣是未定义的, 其中 .
┗ 就是说与实或复线性空间同构以后, 作为线性空间才能谈维度: .
群表示这个 3P 结构我们简记为
✦ 表示矩阵:
在
这里的矩阵
就称为 的 表示矩阵, 显然 是它的逆矩阵.
或者说你干脆把表示
要注意, 所谓的
维线性表示就是把目标集合里的元素映射到 维空间上的线性变换上,
┣ 这个映射要保原集合里有的运算 (即同态), 实空间就是实表示, 复空间就是复表示.
┣ 然后如果存在上的 维实表示,
┣ 则把这些表示矩阵直接搬到上去就成了 维复线性表示了,
┗ 所以这里的维度与表示的实与复的关系并不那么大.
不要觉得复表示的自由度多了一倍之类的.
┣ 同样是维表示, 当讨论实表示时 表示矩阵最多只有 个独立的.
┣ 而讨论复表示的时候, 虽然每个矩阵元都可以放复数了, 但整个表示空间都是复空间,
┗ 所以独立的矩阵还是只有个, 因为叠加系数都是复数了.
再具体点说就是你以为与 是独立的,
┣ 但实际上, 也就是说二者线性相关.
┣ 所以无论实复, 二维表示里就最多四个独立元素,
┣ 然后一般来说实表示不一定存在, 所以我们 (搞物理的) 从来都只考虑复表示.
┗ 只是说恰好复表示矩阵里只有实数或纯虚数时, 能把复表示空间缩到实表示空间罢了.
4.2. 忠实 幺正 正则:
✦ 忠实表示:
若对
其实就是单射呗, 忠实说明靠谱, 你可以极端点考虑把所有群元都映射到单位阵,
┗ 那也是保群乘法的, 但没卵用, 这样丢失信息所以我们才说它不忠实.
有限群必存在忠实表示, 正则表示就是其中一例.
✦ 幺正表示:
若
当然这是选定基矢之后的, 没选定就没有幺正表示了吗? 当然不是, 其实本质定义源于内积:
┣ 对, 有 则称 为 的幺正表示.
┗ 其中表示内积, 用尖括号是因为圆括号在这里不好看.
✦ 正则表示 (regular representation):
对有限群
因为维度等于群阶, 所以就可以将群元与基底一一对应, 即将基矢量记为
这里
表示的是一个与群元 相对应的基矢, 就是一个符号, 没隐含幂运算之类的关系.
┗ 且约定对有 , 就是个约定记号罢了.
规定对
所谓线性变换就是
的映射呗,
┣ 研究映射如何作用在任意矢量上, 只要研究它如何作用在基矢上, 为啥? 因为是线性作用啊.
┣ 那么对能对应一个线性变换 , 它将任意基矢 映射到 .
┗ 这就定义了与群同态的线性变换群.
表示是一个合格的同态映射吗? 显然是的:
┣ 保群乘法:.
┗ 我一开始就说过的, 其实逆元映射到逆元, 单位元映射到单位元其实都是保群乘法的推论.
其实你想想, 正则表示下是不是就是用群元作为基底构建了一个线性空间.
4.3. 群代数:
正则表示里面产生了一个复线性空间
对
有 , 其中 , 是矢量分量的系数.
那么, 某种意义上矢量
✦ 将映射
反过来说, 一个群函数也可以唯一确定一个矢量
.
┣ 那么前面的群阶维复线性表示空间其实就是群函数空间 吧.
┗ 那么很显然,中最多只能有 个线性独立的矢量.
结论: [群中的群函数] 就是 [正则表示 中的一个矢量].
┗ 这里暂不说透, 但可以说这个概念与波函数跟态矢量的关系十分类似, 后面会讲到.
✦ 可以定义矢量乘法: 对
给定矢量
, .
┣ 显然有.
┣ 现在记, 则有:
┣
┣
┗.
上面可不是什么
, 别胡思乱想.
┗ 倒数第二个等号是因为对求完和只剩下 这个变量了.
✦ 综上所述,
代数又称线性代数, 简单来说就是定义有矢量乘法
的线性空间 ,
┗ 乘法有分配律而不要求结合律, 有结合律的代数叫结合代数.
比如说全体方阵可以在矩阵乘法下构成一个线性代数.
✦ 一般人为定义内积
这样就能取矢量系数:
强行狄拉克符号即
是不是很熟悉:.
4.4. 类函数:
✦ 共轭类集合
对
, 是一个集合.
✦ 类函数即满足对
你该不会忘了Ad for adjoint 吧?
.
┣ 这也就是说类函数将一个共轭类映射到同一个复数上, 所以是共轭类的函数, 称之类函数.
┣ 也可以说是轨道的函数:
┗轨道即 .
例如表示矩阵的迹
> 硬要严格一点儿来说的话, 这个其实只是将同类元素都映射到同一个复数上的群函数.
┗ 但很显然这能自然地诱导出一个的类函数吧?
✦ 类函数空间
作为线性空间有
.
定义空间基底
由此对任意类函数
可做分解 : .
┗ 这是显然的:.
要说的话,
这么做其实也是有点儿吃饱了撑的, 我们一般都是反过来干.
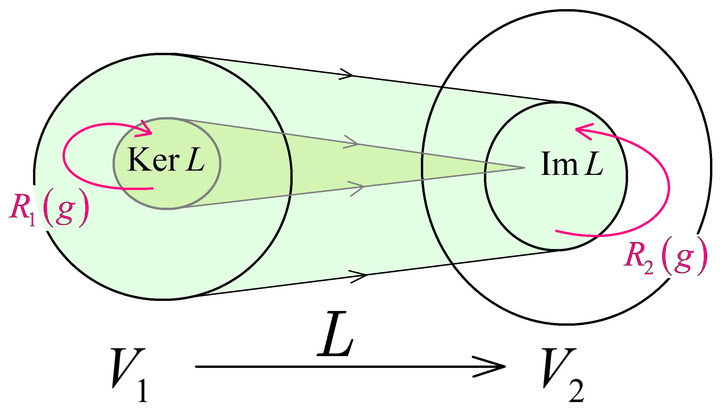
4.5. 等价表示:
✦ 前面说了表示是一个 3P 的过程, 如果两个不同的表示
若
则称
注意这里只有表示不同,
都是相同的.
 就是说两个不同的复合映射将同一个矢量映射到同一个矢量.
就是说两个不同的复合映射将同一个矢量映射到同一个矢量.
✦ 有限群的全部有限维表示都各存在一个与其等价的幺正表示.
幺正表示
就是对 均有 的表示.
不想给严格证明了, 直观感受如下:
┣ 本来线性空间内定义的内积是 .
┣ 我们如果这样换一个新的内积规则.
┣ 则在这套新的规则下,一定是一个幺正表示:
┣> ┣ 这里我们换了一套内积, 其实线性空间内积的取法是不唯一的,
┣ 可以通过选取新的基底来进行内积定义的变换.
┣ 而基底的变换无非就是进行一个相似变换,
┣ 这个相似变换矩阵就可以将等价与一个幺正表示,
┣ 如果你很懂量子力学表象的变换这里也应该能找到点儿感觉.
┣ 想不通也不要深思, 真那么好奇就自己上网冲下浪找找严格证明.
┣ 我自己不想, 也不想让大家花费精力在这里, 只希望大家能记住这个简单的结论.
┗ 这等于说我们最终只需要研究幺正表示就足够了.
4.6. 不可约表示:
✦ 可约与完全可约:
设
是 在 上的表示, 若 使得对 , 有 .
┣ 即中存在关于 不变的真子空间 , 则称 是可约表示.
┗ 更直白点就是,可约 存在子空间 使得 无法将其中任何矢量射出它本身.
设可约, 即有 不变的真子空间 存在,
┗ 若补空间也是不变子空间, 则称 完全可约 (complete reducible).
有限群的可约表示必然是完全可约的.
┗ 这个结论是显然的, 你都看到 4.6 节了, 这点思维量对你来说应该不值一提吧.
✦ 直和:
设
什么叫做子空间呢? 比如说 x-y 平面就是立体直角坐标系的子空间.
┗ 建议回到第一篇文中最开头配合那几个矩阵那儿动动你的奶子好好地想一想.
其实这里稍微有个地方不太严格:
┣ 比如说我们规定.
┣ 假如, 那上面 .
┣ 我们说, 那按理说应该有 才对呀, 怎么维数都变了啊?
┣ 其实吧, 当我们嘴上说时,
┗ 心里却偷偷想的是, 还请理解一下.
✦ 可约分解:
可约的情况下既然子空间都互相不干涉了, 那干脆就把总空间改写成子空间的直和.
即
与 都是 的 不变子空间时, 可以写作 .
再将表示
我们还会这样标记表示的分解:
.
如此一来线性变换就一定是分块对角矩阵:
对
有 ,
┣ 设, 这个时候 中的矢量都是 这样的,
┗ 所以作用上来时不同空间不会互相干涉.
其实这个
最后就有:
这样完全由不可约表示直和成的表示.
┣ 我们还会将上式记作.
┗ 就是说对有 .
4.7. Schur 引理一:
✦ 设
注意表示空间
都是有限维.
证明:
首先说明一下,
分别是映射核 (像中单位元对应的原像集合) 与映射像 (值域).
(我下面这张图画的实在是太漂亮了)
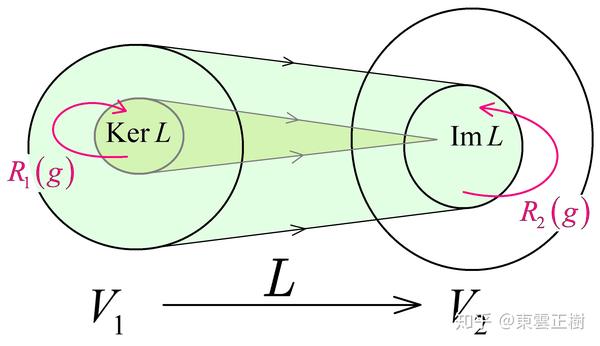 请务必配合我这张精心绘制的图看下面的证明, 因为初学者的想象力还不够丰富.
请务必配合我这张精心绘制的图看下面的证明, 因为初学者的想象力还不够丰富.
Claim:
(下面将证明上面的 Claim, 此过程 暂不考虑不可约 这个条件[6])
┣ 很简单, 题设, 下面设 .
┣ 现在看内部的矢量, 它们全部都是从 被 从射过来的,
┣ 假如其中一个叫的矢量被 射出了 , 即 .
┣ 由题设知必有, 这怎么可能?
┣ 所以不可能将 内任何矢量射出它本身,
┗ 这说明是 的 不变子空间.
┣ 现在看内部的矢量, 它们全部都被 射到 的零元 .
┣ 假如内部有一个 被 射出了 , 即 .
┣ 由题设知必有, 这怎么可能?
┣ 所以不可能将 内任何矢量射出它本身,
┗ 这说明是 的 不变子空间.
这里强调一下, 不变子空间分为三类: (1). 空间本身; (2). 真不变子空间; (3). 只含零元.
接下来我们将利用该 Claim 进行分类讨论:
(1).
首先我们知道
不可约, 说明 里没有 真不变子空间.
┣ 但 Claim 指出是 的 不变子空间.
┣ 那么要么, 要么 呗, 有可能是满射 (即 ) 吗?
┣ 显然像不可能比原像多, 即结合条件有 .
┗ 这也就是说不可能是满射, 那就只能是 了呗, 即 为 映射.
(2).
题设要求
不可约, 这说明 里没有 真不变子空间.
┣ 这也就是说结合 Claim 的话就可知要么, 要么 了呗.
┣ 高维空间往低维空间映射, 那必然有不平凡的映射核, 不觉得显然的话见 [附录D].
┗ 那也就是说所以只有可能是 了呗, 即 为 映射.
(3).
①.
, 由 [附录D] 可知这要求 是单射, 这说明映射可逆,
┣ 既有> ┗ 而这与 不等价这个条件矛盾, 故舍去.
②., 即 为 映射.
综上所述,
两个空间取基底后用矩阵证明会简单很多, 所以这里我选择了相对难证明的版本展示出来.
┗ 矩阵的你可以自己试试, 日后我会补上.
✦ 长话短说版:
俩不等价不可约表示不可能被非零线性变换
像 这样连接起来.
4.8. Schur 引理一的推论:
是受分类讨论第三点启发[7]给出的.
✦ 若存在 非零 线性映射
由 [附录D] 知这要求
是单射, 即映射可逆, 即对 有 .
┗ 这既是说.
✦ 长话短说版: 若有映射满足
4.9. Schur 引理二:
✦
注意这个引理对实表示不一定成立, 然后就是这个表示空间
是有限维的.
┗ 强调复表示目的是保证必存在一个非零本征矢, 记住结论即可, 实在好奇见 [附录E].
证明:
先设
是 的非零本征矢, 本征值为 , 即 .
┣ 再构造映射,
┣ 题设有不难发现也有 .
┣ 令 4.8. 节的推论中的就是现在的情况, 这说明 要么为零要么可逆.
┗怎么可能可逆, 所以 , Q.E.D.
其实还有一个不用推论的直观做法, 但我就是想让你感受到这个推论它很牛啤, 所以放在后面.
直观做法就是说从这个不可约的条件出发, 下面用
代替 , 懂得都懂.
┣说明什么? 有共同的本征矢对吧? 你不会真信了吧, 那要求是厄米算符.
┣ 但我们还是会回想起一些细节:
┣说明 也在 对应的本征子空间里.
┣ 那这个本征子空间现在就有:等矢量.
┣ 你会发现说明 还是在这个本征子空间里.
┗ 那这个本征子空间不就是一个不变子空间吗? 这与 不可约矛盾.
✦ 长话短说版: 只有常数矩阵和零矩阵才能与不可约表示的所有表示矩阵对易.
4.10. 群中心, ker R 与忠实性:
✦ 群中心
就是说
对 都有 ,
┣是理所当然的吧.
┗ 同时显然有关系.
✦ 由 Schur 引理二可知作为线性变换的
✦ 若表示
为何不忠实:
┣.
┣ 上式说明对均有 .
┗ 那要么, 要么就是 不忠实.
✦ 考虑群表示
即
会从一个点扩大成一个非平凡的正规子群, 即 .
┗ 为什么? 因为不就是同态核吗? good ol'同态核定理.
✦ 推论: 群
✦ 没有非平凡正规子群的有限群称为单群 (simple group).
[附录C] 线性空间, 线性变换与内积:
✦ 线性空间:
线性空间
上述
中的 表示直积, 定义 .
上述中的是数域, 参与数乘的数就属于数域, 可以是实数域 或复数域 等.
要注意到顺序是这样的:
┣ 我们是先给定了一个数域,
┣ 然后才给定一个集合,
┣ 集合内定义一个 的二元运算, 称之为矢量加法,
┗ 然后定义一个的数乘运算将 与 耦合起来.
所以谈线性空间的时候要指出是什么域上的线性空间.
矢量加法
下面对
均成立.
┣ (1). 矢量加法的交换律:.
┣ (2). 矢量加法的结合律:.
┣ (3). 存在零元, 即矢量加法的单位元使得 .
┣ (4). 存在矢量加法的逆元使得 .
┣ (5). 存在数乘的单位元使得 .
┣ (6). 数乘与数域乘法相容:.
┣ (7). 数乘对数域加法的分配律:.
┗ (8). 数乘对矢量加法的分配律:.
注意数乘是不要求交换律的, 然后就是数域自带了正常的乘法和加法, 就是小时候玩的那种.
举一例加深理解[10]:
在
上定义运算 .
┗ 若将定义为矢量的加法, 而将 定义为数乘的话 就构成 上的线性空间.
线性空间
实际上,
是线性空间 的唯一的特征量或者说不变量.
┗ 所以两个线性空间只要维度相同我们就可以说它们同构[11]了.
最后, 由于矢量加法与数乘的运算与数域加法乘法相容, 就没必要特意创造新符号了.
就是说我们将用
与 来代替 与 , 这并不会造成任何混乱.
✦ 线性变换:
线性变换就是
关键在于是 线性 的映射, 就很好算, 线性就是说对
均满足:
┗ (1).. (2). .
所有线性变换都可以用方矩阵表示, 所有矢量都可以用列矩阵表示, 文中会证明这一点.
✦ 内积空间:
内积空间就是定义了内积运算的线性空间, 内积本质是一个映射
即对
有 . 而这个映射是人为指定[12]的, 并没有什么玄妙的地方.
然后就是上述映射要满足以下四个关系才能被称作内积运算:
(1).
[13].
(2)..
(3)..
(4)..
✦ 进一步理解参考 [前置内容].
[附录D] 有限高维空间往低维空间线性映射:
✦ 线性映射: 同一个数域
具体而言线性映射要对
可加性:
.
齐次性:.
✦ 有限高维空间往低维空间线性映射:
考察映射
零元一定被映射到零元, 即对
均有:
┗.
逆元一定被映射到逆元, 即对有:
┗.
高维度往低维映射不可能是单射吧, 那么就必存在不相同的使得 .
┣ 显然, 此时有 .
┗ 这就说明映射核是非平凡的.
[附录E] 复空间线性变换至少有一个非零本征矢:
已知
然后方程
行列式值为零说明如果我们将它的每列当作一个矢量, 即
那么这组矢量一定是线性相关的.
而线性相关的定义就是存在一组不全为零的数使得
那么这组数构成的矢量
因为
也就是说有
评论:
海森堡的小迷弟: 看到3p直接举报ghs[惊喜][惊喜] (24 赞)
Dieucra: 怎么你们学物理的人均阴间作息) (10 赞)
東雲正樹 -> Dieucra: 🌿我早上还有课, 怎么就早上了呢. (5 赞)
知乎用户:
根据第一段,就是在玩Cosplay啊!还不给配个好图[机智]
查看图片 (8 赞)
知乎用户: 太高产了吧欢呼 (1 赞)
東雲正樹 -> HelgaE: 我真的一滴也不剩了, 下一篇要⋯ (10 赞)
Young Quantum -> 東雲正樹: 下一篇要今天晚上出[滑稽] (6 赞)
東雲正樹 -> Young Quantum:
那出的不是 note 了是人命.
查看图片 (4 赞)
Young Quantum -> 東雲正樹: [看看你]拼命的男孩子女生最喜欢了 (4 赞)
Triborg -> 東雲正樹: 人命?有两亿[好奇][调皮][调皮][调皮] (1 赞)
東雲正樹 -> Triborg:
那不是人命那是
查看图片 (1 赞)
Triborg -> 東雲正樹: 哦? 查看图片 (1 赞)
知乎用户:
“这个结论是显然的, 你都看到 4.6 节了, 这点思维量对你来说应该不值一提吧”
完全看不出有限群的条件在这里有什么用
東雲正樹 -> CherryWull: 查看图片
東雲正樹 -> 東雲正樹: 查看图片
東雲正樹 -> 東雲正樹: 查看图片
无笑作业 -> 東雲正樹: 《 不 值 一 提 》[可怜]
東雲正樹 -> 无笑作业:
我感觉好显然⋯
查看图片
无笑作业 -> 東雲正樹: 不愧是🌴[大哭]
Young Quantum: 好家伙,我这昨天半晚催,你这当天就出啊[捂脸] (4 赞)
士不可以不弘毅: “群表示是个3P结构”,开幕雷击 (3 赞)
无笑作业: 所以GL(V)既是一个无限群,又是一个dim<=n^2的线性空间?
東雲正樹 -> 无笑作业: GL(V) 不行, 这里面的元素都要可逆. End(V) 的话就是线性空间.
東雲正樹 -> 无笑作业:
当然如果你想的那个线性空间不是 End(V) 而是定义连续线性变换或者说矩阵乘法为矢量加法能否构成线性空间的话,
你可以自己验证一下满不满足线性空间的八条运算法则, 满足就行, 但没用.
无笑作业 -> 東雲正樹: 哦哦,好吧
我小朋友谢谢: 感谢作者!非常清晰帮助很大!另请问一下作者,正则表示那里选取的基矢量的上标是指角标么?应该这里的上标不是幂次吧
東雲正樹 -> 我小朋友谢谢: 不是幂, 这里一开始没有乘法运算呢.
東雲正樹 -> 東雲正樹: 而且群元次幂也没意义呀, 就是一个记号一样的东西, 也不具备缩并之类的功能.
我小朋友谢谢 -> 東雲正樹:
好嘞多谢啦!
一童天下: 但是大佬,,只会这些还是感觉不够啊。。。物理群论很多篇幅都是处理各种具体的群与物理应用。。。 (1 赞)
東雲正樹 -> 一童天下: 还没出新手村呢. (7 赞)